✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,代码获取、论文复现及科研仿真合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
🔥 内容介绍
在现代物流领域,车辆路径规划是一个重要的问题。它涉及到如何有效地分配车辆并规划它们的路径,以满足客户需求,并最大程度地降低成本。然而,车辆路径规划问题并不简单,尤其是在考虑到时间窗口的情况下。
时间窗口是指客户对车辆到达时间的限制。例如,某些客户只能在特定的时间段内接受货物交付。因此,为了满足客户需求,车辆路径规划问题必须考虑到时间窗口约束。
为了解决这个问题,遗传算法(Genetic Algorithm,GA)被广泛应用。遗传算法是一种模拟自然进化过程的优化算法,它通过模拟生物的遗传和进化过程来搜索最优解。
在GA-VRPTW中,我们首先需要定义问题的适应度函数。适应度函数用于评估每个个体(车辆路径规划方案)的优劣程度。在车辆路径规划问题中,适应度函数通常包括两个方面的考虑:路程和时间。
对于路程方面,我们可以使用总路程的长度来评估一个路径规划方案的优劣。较短的总路程意味着更高的效率和更低的成本。
对于时间方面,我们需要考虑每个客户的时间窗口约束。如果一个车辆到达某个客户的时间超出了其时间窗口的范围,那么这个路径规划方案就是无效的。因此,我们需要将时间窗口约束纳入适应度函数的计算中。
在遗传算法的迭代过程中,我们使用选择、交叉和变异等操作来生成新的个体。选择操作通过评估个体的适应度来决定哪些个体将被选择为下一代的父代。交叉操作通过交换父代个体的基因来生成新的个体。变异操作通过随机改变个体的基因来引入新的变化。
通过不断迭代和优化,遗传算法能够找到一个较优的车辆路径规划方案。这个方案能够满足客户需求,同时最大程度地降低成本和提高效率。
然而,虽然遗传算法在解决VRPTW问题上表现出一定的优势,但它也存在一些局限性。例如,遗传算法可能陷入局部最优解,导致无法找到全局最优解。此外,遗传算法的计算复杂度较高,需要大量的计算资源和时间。
为了克服这些问题,研究人员不断提出改进的遗传算法和其他优化算法。例如,可以使用多目标遗传算法来解决多目标车辆路径规划问题。此外,还可以将遗传算法与其他启发式算法相结合,以提高求解效率。
总的来说,基于遗传算法的车辆路径规划问题求解(GA-VRPTW)是一个具有挑战性的问题。它涉及到在满足客户需求的同时,最大程度地降低成本和提高效率。通过不断改进遗传算法和其他优化算法,我们可以更好地解决这个问题,并为物流行业带来更大的效益。
📣 部分代码
%% 删除种群中重复个体,并补齐删除的个体
% 输入Chrom:种群
% 输出dChrom:处理掉重复个体的种群
function dChrom=deal_Repeat(Chrom)
N=size(Chrom,1); %种群数目
len=size(Chrom,2); %染色体长度
dChrom=unique(Chrom,'rows'); %删除重复数组对
Nd=size(dChrom,1); %剩余个体数目
newChrom=zeros(N-Nd,len);
for i=1:N-Nd
newChrom(i,:)=randperm(len);
end
dChrom=[dChrom;newChrom];
end
⛳️ 运行结果
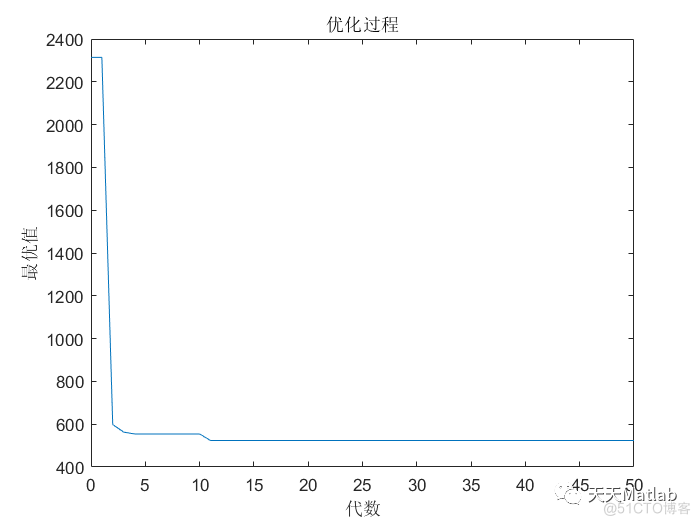
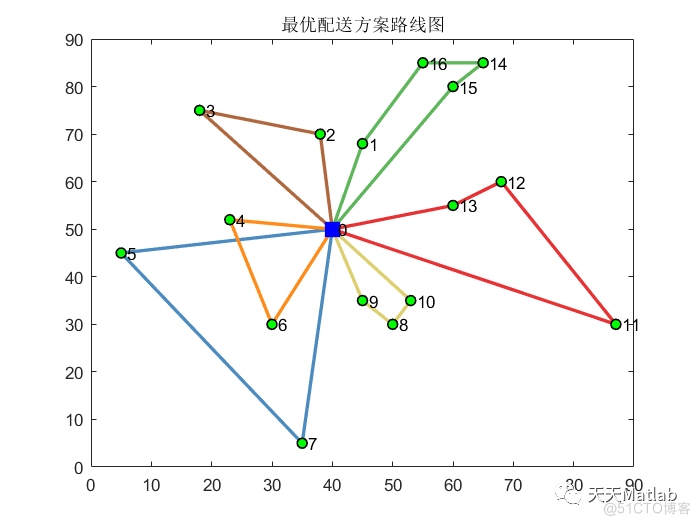
🔗 参考文献
[1] 张露.基于改进遗传算法求解带时间窗车辆路径规划问题[J].中国物流与采购, 2020(14):4.
[2] 王毅.物流配送系统车辆路径规划问题研究[D].华南理工大学,2009.DOI:10.7666/d.Y1593615.




 文章探讨了遗传算法在解决车辆路径规划问题(VRPTW)中的应用,特别是考虑时间窗口约束的情况。通过定义适应度函数和迭代优化过程,遗传算法寻求成本最低、效率最高的路径。文章还提到了遗传算法的局限性和改进方法,以及在物流领域的实际意义。
文章探讨了遗传算法在解决车辆路径规划问题(VRPTW)中的应用,特别是考虑时间窗口约束的情况。通过定义适应度函数和迭代优化过程,遗传算法寻求成本最低、效率最高的路径。文章还提到了遗传算法的局限性和改进方法,以及在物流领域的实际意义。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








