💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学,什么是电的时候,不要觉得这些问题搞笑。哲学是科学之母,哲学就是追究终极问题,寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能让人胸中升起一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它居然给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
文献来源:

摘要:
本文涉及跟踪扩展对象或群组目标,这会导致来自不同测量源的测量数量变化。为此,除了目标的运动学,还会跟踪目标的形状。目标范围采用一种称为随机超曲面模型(RHM)的新方法建模,该方法假设不同的测量源位于形状边界的缩放版本上。本文介绍了用于跟踪星凸近似形状目标的星凸RHM。通过高斯假设的状态估计器进行星凸RHM的贝叶斯推理,从而实现了一种高效的递归闭合形式测量更新。模拟展示了该方法在典型扩展对象和群组跟踪场景中的性能。
典型的目标跟踪建模假设是目标是一个没有范围的数学点。然而,在现实世界的跟踪系统中,有两种主要场景不适用于这一标准假设。
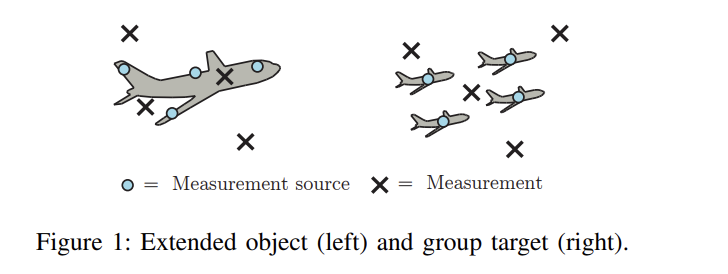
首先,现代传感器设备(如雷达设备)的分辨率通常比目标物体的空间范围更高(参见图1)。因此,在单次扫描中可能会解析出目标物体上的几个未知点,即测量源。这些测量源可能会从一次扫描到另一次扫描变化,并且它们的位置不仅取决于目标的形状,还取决于更复杂的目标特性(如表面的性质)甚至目标与传感器的几何关系。
其次,作为一个单一实体考虑的一组点目标可以被看作是一个整体,因为各个成员之间存在着高度相互依赖性,这由群体行为规定。同样,在这种情况下,测量源会在每次扫描中变化,并且它们的位置高度依赖于群体的属性(例如群体之间的几何关系)。
在这种意义上,扩展物体可以被定义为具有共同属性的一组测量源,例如动态行为或状态变量。如果这组测量源由有限的测量源组成,则称为群体目标[1]。然而,在连续的测量源组成的情况下,则称为扩展物体。根据这一定义,扩展物体和群体跟踪包括跟踪形成目标的一组测量源。
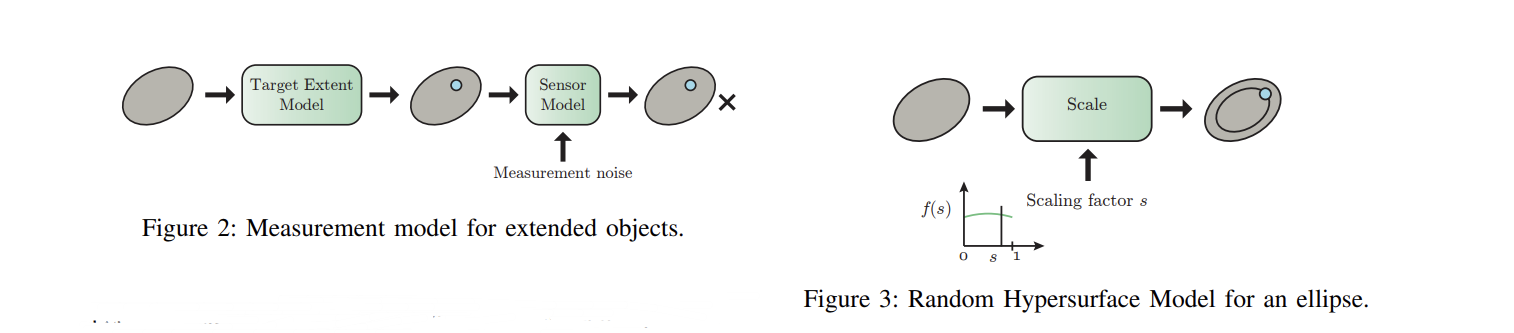
扩展物体与群体目标的形状跟踪及星凸RHMs研究进展
一、扩展物体跟踪的核心概念与技术特点
扩展物体(Extended Objects)指在传感器分辨率下占据多个检测单元的目标(如车辆、无人机群等),需同时估计其运动状态(位置、速度)和扩展状态(形状、尺寸、方向)。其核心特征包括:
- 多量测特性:高分辨率传感器(如激光雷达、毫米波雷达)每次扫描可获取同一目标的多个反射点,形成目标轮廓的离散采样。
- 形状建模需求:传统点目标模型无法利用空间分布信息,需引入参数化(如椭圆、矩形)或非参数化形状模型(如样条曲线、高斯过程)。
- 分类与跟踪融合:形状特征可辅助目标分类,例如通过傅里叶级数展开的径向函数区分车辆与行人。
典型方法:
- 随机矩阵模型(RMM) :用对称正定矩阵描述椭圆轮廓,适用于简单形状的实时跟踪。
- 随机超曲面模型(RHM) :通过随机缩放边界建模复杂形状,支持星凸形目标的参数化表示(如径向函数r(pk,ϕ)结合傅里叶级数展开)。
- 水平集高斯过程:非参数化方法,适用于非星凸形目标,通过隐式曲面描述复杂轮廓。
二、群体目标跟踪的技术挑战与建模策略
群体目标(Group Targets)指以协同方式移动的多个子目标(如无人机集群、鸟群),其特点包括:
- 动态结构:子目标数量、空间分布及运动模式随时间变化,可能发生分裂、合并等行为。
- 数据关联复杂性:密集目标导致测量点与个体间的关联模糊,需结合聚类(如DBSCAN)与多假设跟踪(MHT)。
- 形状与运动耦合:群体整体形状(如编队队形)与个体轨迹需联合估计。
关键方法:
- 随机有限集(RFS)框架:将群体状态建模为随机集,避免显式数据关联,支持新生/消亡目标处理。
- 多伯努利滤波器:基于势均衡的多目标跟踪算法,适用于可分辨群体(如泊松多伯努利混合滤波器)。
- 交互模型:引入马尔可夫链蒙特卡洛(MCMC)或信念传播(Belief Propagation)处理子目标间的运动约束。
三、星凸随机超曲面模型(RHM)的数学定义与作用
星凸RHMs是一种专为复杂形状设计的参数化模型,其核心原理为:
-
形状参数化:星凸集合S(pk)S(pk)由中心点mkmk和径向函数r(pk,ϕ)定义,其中ϕ为极角,pk为傅里叶系数向量。
-
量测生成模型:量测点zk,lzk,l由边界缩放因子sk,l和噪声vk,l生成:
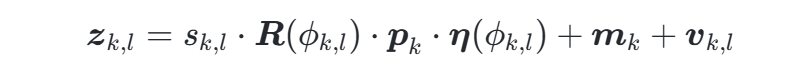
其中R(ϕ)为旋转矩阵,η(ϕ)为单位方向向量。
-
状态估计:结合容积卡尔曼滤波(CKF)或Unscented Kalman滤波(UKF)实现非线性状态更新,同步优化运动状态与形状参数。
优势:
- 灵活性:通过傅里叶级数可逼近任意星凸形状,支持从椭圆到复杂多边形的建模。
- 计算效率:参数化表示减少计算复杂度,适用于实时跟踪场景。
- 抗噪能力:随机缩放因子sk,lsk,l可缓解传感器噪声对形状估计的影响。
四、形状跟踪与星凸RHMs的协同机制
-
扩展物体与群体的统一建模:
- 当群体紧密排列时(如无人机编队),可视为单一扩展物体,采用RHM描述整体形状。
- 群体分裂时,RHMs可快速重构子群体形状,结合RFS框架处理目标数目变化。
-
关键技术融合:
- 动态形状自适应:利用高斯过程(GP)在线更新径向函数,适应群体形状的实时变化(如鸟群扩散)。
- 多传感器融合:在激光雷达与相机数据融合中,RHMs提供形状先验,提升遮挡场景下的跟踪鲁棒性。
- 深度学习增强:引入Transformer网络提取形状特征,解决机动目标导致的模型失配问题(如文献[22]中基于自注意力机制的形状预测)。
-
典型算法:
- RHM-CKGM-ETCBM-eMBer滤波器:结合多伯努利框架与容积卡尔曼滤波,实现多扩展目标的形状与运动联合估计。
- RHM-CC-IOU-UKF:通过交并比(IOU)检测形状突变,动态调整滤波参数以应对群体重组。
五、研究难点与未来方向
-
跨尺度建模:
- 挑战:扩展物体形状细节(如车辆轮廓)与群体宏观结构(如编队队形)需分层建模,但参数共享易导致过拟合。
- 解决思路:引入多分辨率RHMs,结合小波分解实现形状特征的多尺度表达。
-
高维非线性优化:
- 挑战:星凸参数(傅里叶系数)与运动状态(位置、速度)联合优化时,高维状态空间导致粒子滤波退化。
- 进展:基于变分推断的稀疏高斯过程回归(SVGP),在保证精度的同时降低计算量。
-
评估指标缺失:
- 现状:现有指标(如OSPA距离)难以量化形状估计误差,尤其对非凸轮廓。
- 新方法:提出基于Hausdorff距离的形状相似度度量,结合轮廓曲率分布分析。
-
应用场景拓展:
- 军事领域:弹道导弹群目标跟踪中,RHMs需平衡分裂检测与形状稳定性(见文献[16]中的帕累托优化策略)。
- 民用领域:人群密度估计中,将星凸RHMs与热力图融合,实现遮挡场景下的实时计数。
六、总结
扩展物体与群体目标的形状跟踪正从单一椭圆建模向非参数化、自适应化方向发展。星凸RHMs通过参数化与非线性滤波的结合,在复杂形状估计中展现出独特优势,但其与群体结构建模的深度融合仍需解决动态耦合、计算复杂性和评估标准化等挑战。未来研究或将聚焦于多模态传感器融合、轻量化深度学习架构与新型形状描述符的开发。
📚2 运行结果
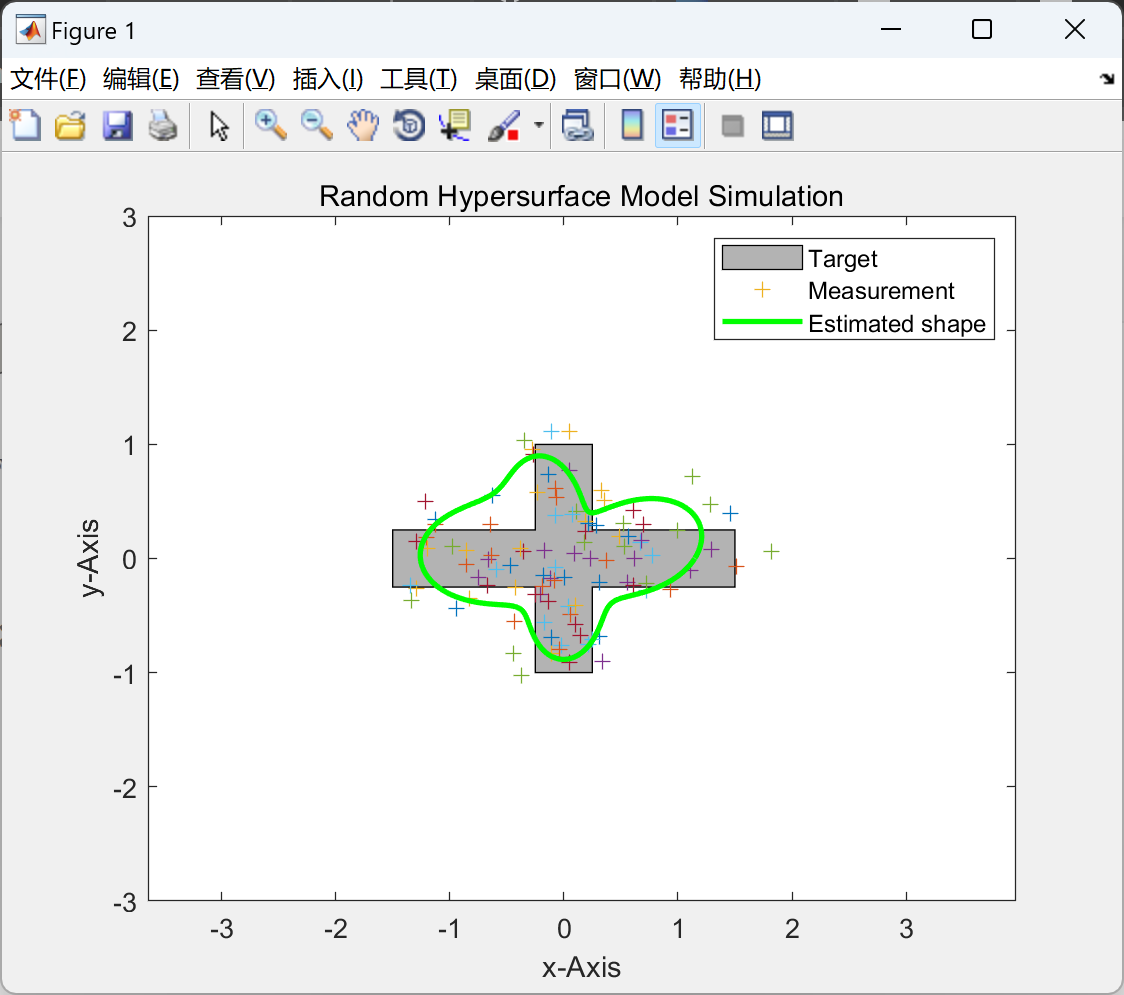
部分代码:
% Calculate Sigma Points
%Stack state and noise mean
x_ukf = [x; measurementNoiseMean];
%Stack state and noise Covariance
C_ukf = blkdiag(C, measurementNoiseCovariance);
n = size(x_ukf, 1);
n_state = size(x, 1);
lamda = alpha^2 * (n + kappa) - n;
% Calculate Weights Mean
WM(1) = lamda / (n + lamda);
WM(2 : 2 * n + 1) = 1 / (2 * (n + lamda));
% Calculate Weights Covariance
WC(1) = (lamda / (n + lamda)) + (1 - alpha^2 + beta);
WC(2 : 2 * n + 1) = 1 / (2 * (n + lamda));
%Calculate Sigma Points
A = sqrt(n + lamda) * chol(C_ukf)';
xSigma = [zeros(size(x_ukf)) -A A];
xSigma = xSigma + repmat(x_ukf, 1, size(xSigma, 2));
% Filterstep
z = 0;
C_yy = 0;
C_xy = 0;
zSigmaPredict = feval(measurementFunctionHandle, xSigma(1:n_state,:), xSigma(n_state + 1:n, :), measurement, numberOfFourierCoef );
for i = 1 : size(zSigmaPredict, 2);
z = z + ( zSigmaPredict(:,i) * WM(i) );
end
for i = 1 : size(zSigmaPredict, 2)
C_yy = C_yy + WC(i) * ( (zSigmaPredict(:,i) - z ) * ( zSigmaPredict(:,i) - z )') ;
C_xy = C_xy + WC(i) * ( (xSigma(1:size(x, 1),i) - x ) * ( zSigmaPredict(:,i) - z )');
end
K = C_xy / C_yy;
x_e = x + K * (zeros(size(z)) - z);
C_e = C - K * (C_yy) * K';
end
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
M. Baum and U. D. Hanebeck, "Shape tracking of extended objects and group targets with star-convex RHMs," 14th International Conference on Information Fusion, Chicago, IL, USA, 2011, pp. 1-8. keywords: {Shape;Target tracking;Noise measurement;Shape measurement;Bayesian methods;Radar tracking;Mathematical model;Target tracking;shape tracking;extended objects;group targets},




















 1441
1441

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








