《算法图解》第一章——算法简介

最新推荐文章于 2023-12-05 21:08:37 发布

ML_akai

最新推荐文章于 2023-12-05 21:08:37 发布

阅读量434

点赞数

CC 4.0 BY-SA版权

分类专栏：算法图解文章标签：算法基础

本文链接：https://blog.youkuaiyun.com/ML_akai/article/details/83277239

算法图解专栏收录该内容

4 篇文章

订阅专栏

本文深入解析二分查找算法及其优势，对比简单查找，阐述大O表示法在评估算法效率中的应用。通过实例，展示二分查找如何在更少的操作下找到目标元素，同时解释了算法运行时间的增速概念。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

补足基本功，特此作为读书记录。特此感谢深度眸博主的资料与博客技术分享

资料链接：http://cuijiahua.com/resource.html

二分查找

书中以一个例子引入该算法。例：在一个电话簿中找名字以K打头的联系人，方法一：从头开始翻直到以K打头的该联系人。(简单查找)；方法二：先从中间找翻到字母K，然后再去找该联系人(二分查找)。需要注意的是：电话本一定是已经按照A到Z的顺序排好序的，不然方法二将无法实现。

二分查找是一种算法：输入一个有序的元素列表。如果要查找的元素包含在列表中，二分查找返回其位置；否则返回null

图1. 图解二分查找法

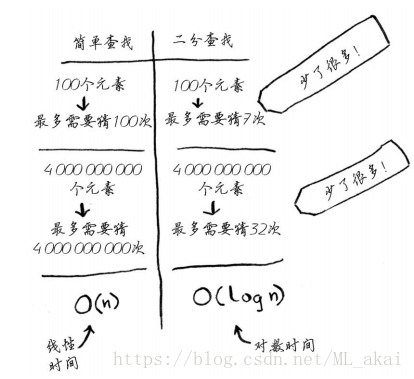
书中接着提出个问题，来练习加强理解该算法，例：1~100让你猜数字，每次你猜测后我会说大了还是小了还是对了。两种解决方法如下：一.简单查找（傻找）：从数字1开始猜，每次排除一个数字，直到猜测正确；二.二分查找：每次都从中间猜，每次排除一半，直到猜测正确。所以如果所猜数字是99的话，那么我们用法一将会进行99次操作，而使用二分法，则最多进行7次操作。二分查找法的优势凸显出来了。

一般而言，对于包含n个元素的列表，用二分查找最多需要log2n步，而简单查找最多需要n步

测试代码如下：

#!/usr/bin/env python3 
# -*- coding:utf-8 -*-
def binary_search(list,item): #两个位置参数
    low = 0      #列表的头
    high = len(list)-1  #列表的尾
    while low <= high:  #循环条件
        mid = int((low + high) / 2) #获取列表的中间位置
        guess = list[mid]
        if guess == item:
            return mid
        if guess > item:
            high = mid - 1
        else:
            low = mid + 1
    return None
        
my_list = range(1,101)
print(binary_search(my_list,7)) #测试7在哪里
print(binary_search(my_list,-1))#测试-1在哪里