算法3.1 影响力扩展度的蒙特卡洛模拟
1. 介绍
计算影响力拓展度的一个简单的方法是反复模拟在某个种子结点集合SSS之下影响力的传播过程,统计这些模拟过程中被激活结点个数的平均值,用这个平均值作为种子集合SSS的影响力扩展度σ(S)σ (S)σ(S)的估计值。这种模拟估计的方法通常被称为蒙特卡洛模拟(Monte Carlo Simulation)。
2.伪代码:

流程图

3. 示例代码
import random
import networkx as nx
import matplotlib.pyplot as plt
# 模拟影响力传播
def simulate_influence_spread(G, seed_set, propagation_prob):
activated = set(seed_set) # 初始化激活节点
newly_activated = set(seed_set) # 当前轮次刚刚被激活的节点
while newly_activated:
next_round = set()
for node in newly_activated:
for neighbor in G.neighbors(node):
if neighbor not in activated and random.random() < propagation_prob:
next_round.add(neighbor) # 以传播概率激活邻居节点
newly_activated = next_round
activated.update(newly_activated) # 更新已激活的节点
return activated # 返回最终被激活的节点集合
# 蒙特卡洛模拟影响力扩展度
def monte_carlo_influence_spread(G, seed_set, T, propagation_prob):
total_spread = 0 # 用于累计传播的节点数量
for _ in range(T):
activated_nodes = simulate_influence_spread(G, seed_set, propagation_prob)
total_spread += len(activated_nodes) # 累加每次传播的影响节点数量
# 计算影响力扩展度的平均值
average_spread = total_spread / T
return average_spread
# 可视化函数
def visualize_influence_spread(G, seed_set, activated_nodes):
pos = nx.spring_layout(G) # 使用 Spring 布局
plt.figure(figsize=(8, 6))
# 绘制所有节点
nx.draw_networkx_nodes(G, pos, node_color='lightgrey', node_size=50)
# 绘制种子节点
nx.draw_networkx_nodes(G, pos, nodelist=seed_set, node_color='red', node_size=300, label='Seeds')
# 绘制被激活的节点
nx.draw_networkx_nodes(G, pos, nodelist=activated_nodes, node_color='green', node_size=300, label='Activated')
# 绘制未被激活的节点
non_activated_nodes = set(G.nodes()) - activated_nodes - set(seed_set)
nx.draw_networkx_nodes(G, pos, nodelist=non_activated_nodes, node_color='lightblue', node_size=50, label='Non-activated')
# 绘制节点之间的边
nx.draw_networkx_edges(G, pos, alpha=0.3)
# 绘制节点标签
nx.draw_networkx_labels(G, pos, font_size=8)
# 图例
plt.legend(scatterpoints=1)
plt.title("Influence Spread Visualization")
plt.show()
# 示例使用:生成一个小图
G = nx.erdos_renyi_graph(100, 0.05) # 生成一个包含100个节点和边的随机图
seed_set = [0, 1, 2] # 假设选择节点 0, 1, 2 作为种子节点
T = 100 # 模拟次数
propagation_prob = 0.3 # 传播概率
# 进行蒙特卡洛模拟
average_spread = monte_carlo_influence_spread(G, seed_set, T, propagation_prob)
print(f"平均影响力扩展度: {average_spread}")
# 可视化种子节点和影响力传播结果
activated_nodes = simulate_influence_spread(G, seed_set, propagation_prob)
visualize_influence_spread(G, seed_set, activated_nodes)
4. 结果展示
平均影响力扩展度: 65.44
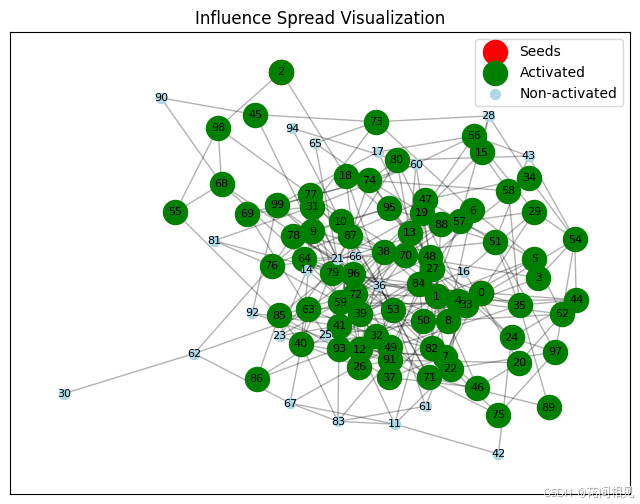






















 6558
6558

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










