基于局部域的影响力最大化算法——文章解析

一、文章摘要

        影响力最大化问题是社交网络分析领域的热点研究问题，而对影响力进行全面科学的度量又是该问题的核心。本文针对度量影响力的全局性指标和局部性指标存在的不足，根据三度分隔原理，提出用节点在局部域内的影响力近似其在全局范围内的影响力并据此进行种子选择的方法。该方法充分利用网络中存在的自环和多边现象，结合网络拓扑结构构建生成图。依据生成图为每个节点划分以其为中心的局部域，用节点在该局部域内的影响力近似其在全局范围内的影响力，并据此去选择候选种子节点。然后，计算候选种子加入种子集合后的重叠比因子，根据该因子决定是否将此候选种子节点选作种子，以此来控制种子集合的影响力重叠程度。在真实数据集上的实验结果验证了本文方法的正确性和有效性。

二、知识介绍

        1.什么是影响力最大化算法

        影响力最大化问题旨在从社交网络中寻找K个最具影响力的节点，使得以这些用户作为种子开始传播信息时信息的最终传播范围最大。影响力最大化问题是从网络中找到一个大小为的节点集合，使得以这个节点作为种子开始影响力传播时影响力的最终传播范围最大（即激活的节点数最多）。影响力最大化问题可由式(1)表示。在式(1)中，表示节点集合，表示影响力的传播范围。

                     (1)

        2.什么是影响力度量

        对用户的影响力进行科学准确的度量是影响力最大化问题的核心之一。网络拓扑结构是影响力度量的重要依据。

        3.影响力度量方法的分类

        网络拓扑结构是影响力度量的重要依据。与拓扑结构相关的影响力度量指标可以分为全局性指标和局部性指标。介数中心性、接近中心性[、离心中心性、流介数中心性、Katz中心性、连通介数中心性等都属于全局性指标。全局性指标需要依靠网络完整拓扑结构，在整个网络范围内计算节点影响力，因此时间复杂度会很高。

        度中心性、半局部中心性、特征向量中心性等都属于局部性指标。这类指标仅依据局部范围的拓扑信息计算节点的影响力。与全局性指标相比，这些局部性指标时间复杂度相对较低。

        4.三度分隔理论

       根据Chrisakis等人的研究成果，影响力传播遵循三度分隔原理，即节点的影响力在相距不超过三跳的邻居节点间传播时随着距离的增大而不断衰减，当传播距离超过三跳时则几近消失。

        5.影响力传播模型

        线性阈值模型（Linear Threshold Model，LT模型）可以用来模拟影响力的传播过程。在LT模型中，节点只能处于激活状态或者非激活状态。激活状态的节点通过有向边试图激活处于非激活状态的邻居节点。而对于非激活状态的节点，当所有激活状态的邻居节点对其影响力之和大于该节点的激活阈值时，该非激活节点就转为激活状态。当网络中不会再有节点被激活时即由非激活状态转为激活状态时，影响力的传播过程收敛。

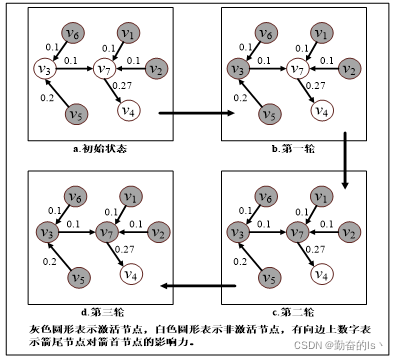
三、本文创新点

        本文针对度量影响力的全局性指标和局部性指标存在的不足，结合三度分隔原理，提出用节点在局部范围内的影响力近似其在全局范围内影响力的方法。该方法首先根据网络拓扑结构构造生成图，依据生成图划分每个节点对应的局部域，根据节点在对应局部域内的影响力筛选候 选种子节点；然后计算每个节点与种子集合的重叠比因子，并据此决定候选种子节点是否能成为种子节点。在真实数据集上的实验结果验证了本文方法的正确性和有效性。

四、本文创新的概念和公式

        1.自环

        自环指的是一种特殊的环结构，这种环状结构只包含一个节点。社交网络中用户可能发起只有自己参与的社交活动，从而在对应的社交网络图中形成只有该节点参与的自环。自环多的节点活跃度较高，在信息传播过程中会主动地影响其他节点。本文引入了自环因子度量自环对节点能力的影响。自环因子根据式(2)计算。在该式中，