贪心算法的改进

关于贪心算法，请看我的上一篇博客。

1. 1. 1. 解决贪心算法的复杂度

为解决贪心算法的复杂度。本文提出：通过分解极大联通子图去寻找影响力最大的节点的算法。

强连通：在有向图G中，如果任意两个不同的顶点相互可达，则称该有向图是强连通的。

极大强连通子图：G 是一个极大强连通子图当且仅当 G 是一个强连通子图且不存在另一个强连通子图 G’使得 G 是 G’的真子集。也就是说不可能找到一个包含它的强连通分量。若将有向图中的强连通分量都缩为一个点，则原图会形成一个 DAG（有向无环图）

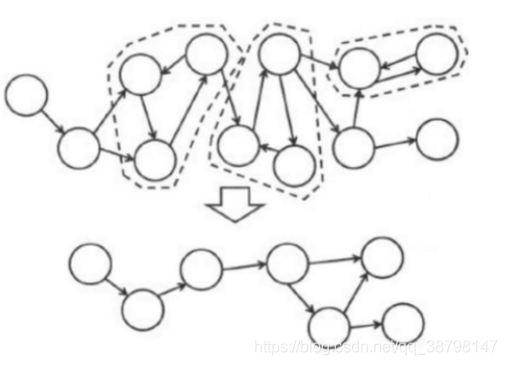
该改进算法是基于对图深度优先搜索(DFS)的算法，每个强连通分量为搜索树中的一棵子树（的一部分）。搜索时，把当前搜索树中未处理的结点加入一个栈，对于每一个结点，当它自己搜索完毕时判断是否存在强连通分量。

算法：void dfs(int u)

{

    times++;//记录dfn顺序

    dfn[u]=times;//赋值

    low[u]=times;//先赋初值

    vis[u]=true;//vis[i]用来判断i是否搜索过；

    insta[u]=true;//表示是否在栈中，true为在栈中；

    stack[top]=u;//栈顶

    top++;

    for(int i=head[u];i!=-1;i=edge[i].next)// 以建图顺序枚举此点所连的边

    {

        int v=edge[i].to;//搜索到的点

        if(!vis[v])//如果未搜索过即未入栈

        {

            dfs(v);//继续以此点进行深搜

            low[u]=min(low[u],low[v]);//更新low值，此边为树枝边所以比较u此时的

        }                           // low值(未更新时就是其dfn值)和v的low值

        else

            if(insta[v]==true)//如果搜索过且在栈中，说明此边为后向边或栈中横叉边

            {

                low[u]=min(low[u],dfn[v]);//更新low值，比较u此时的low值和v的dfn值

            }

    }

    if(low[u]==dfn[u])//相等说明找到一个强连通分量

    {

        while(top>0&&stack[top]!=u)//开始退栈一直退到 u为止

        {

            top--;

            insta[stack[top]]=false;

        }

    }

}

分解完之后再用上述贪心算法。

1. 1. 1. 改进LT模型，重复使用贪心算法

在LT模型的基础上：计算边的权重，计算每个节点AP的值，选择前k/2个节点，贪心算法再选择后k/2个节点。减小了计算的复杂度，增加权重和AP值使模型更可靠。

#计算图中边的权重

def Buv_calculate(G,u,v):

    out_deg_all = G.out_degree()  # 获取所有节点的出度

    in_edges_all = G.in_edges()  # 获取所有的入边

    out_deg = out_deg_all[u]  # 获取节点e[0]的出度

    in_edges = in_edges_all._adjdict[v]  # 获取节点e[1]的所有的入边

    edges_dict = dict(in_edges)

    in_all_edges = list(edges_dict.keys())  # 获取节点e[1]的所有入边节点并存入列表

    out_deg_sum = 0

    for i in in_all_edges:  # 求节点e[1]所有入边节点的出度和

        out_deg_sum = out_deg_sum + out_deg_all[i]

    return out_deg / out_deg_sum

 

#计算每个节点AP的值

def AP_calculate(node):

    data = []

    data.append(node)

    layer_two_nodes = linear_threshold(G, data, 2)  # 获取每个节点的两层出度节点数

    data.pop()

    del layer_two_nodes[-1]

    length = 0

    for i in range(len(layer_two_nodes)):

        length = length + len(layer_two_nodes[i])

    lengths = length - len(layer_two_nodes[0])

 

    out_edges = out_edges_all._adjdict[node]  # 获得节点的出边

    edges_dict = dict(out_edges)

    out_all_edges = list(edges_dict.keys())  # 将节点的所有出边存入列表

    Buv_sum = 0

    for out_edge in out_all_edges:   # 计算该节点所有出边的Buv的值

        Buv = Buv_calculate(G, node, out_edge)

        Buv_sum = Buv_sum + Buv

    cha_sum = 1 + math.e ** (-Buv_sum)

    AP = lengths + cha_sum

    return AP

 

def select_layers(G,node_list_sorted,k1):   #选择前k/2个节点的算法实现

    seed_nodes = []  # 存贮种子节点

    for i in range(k1):

        data = []

        data.append(node_list_sorted[0][0])

        seed_nodes.append(node_list_sorted[0][0])

        layers = linear_threshold(G, data)        # 使用LT算法

        data.pop()

        del layers[-1]

        layers_activate = []

        for i in layers:  # 将种子节点和激活的节点存入layers_activate列表

            for j in i:

                layers_activate.append(j)

 

        for m in node_list_sorted:  # 删除node_list_sorted中的layers_activate

            for n in layers_activate:

                if m[0] == n:

                    node_list_sorted.remove(m)

 

    return seed_nodes,node_list_sorted

 

def _select_others(seed_nodes, other_nodes,k2):     #贪心算法选择剩余k/2个节点

    for m in range(k2):

        all_nodes = list(other_nodes)   #将所有的节点存储在all_nodes列表里

        layers_activite = []    # 存储每个节点的激活节点列表

        lengths = []         # 存储每个节点的激活列表长度

        datas = []

        for i in all_nodes:   #遍历所有的节点，分别求出每个节点对应的激活节点集以及激活节点集的长度

            data = []

            data.append(i)

            datas.append(i)

            data_test=seed_nodes+data

            layers = linear_threshold(G,data_test)

            data.pop()

            del layers[-1]

            length = 0

            layer_data = []

            for j in range(len(layers)):

                length = length + len(layers[j])

                layer_data = layer_data + layers[j]

            length_s = length - len(layers[0])

            for s in range(len(layers[0])):

                del layer_data[0]

            layers_activite.append(layer_data)

            lengths.append(length_s)

        layers_max = layers_activite[lengths.index(max(lengths))]  # 获取被激活节点数最多的列表

        seed_nodes.append(datas[lengths.index(max(lengths))])      # 获取被激活节点最多的子节点

        for i in all_nodes:       #该循环是删除所有节点中seed_nodes节点集

            if i in seed_nodes:

                del all_nodes[all_nodes.index(i)]

        other_nodes=all_nodes

    return seed_nodes,layers_max     #返回值是贪心算法求得的子节点集和该子节点集激活的最大节点集