激光雷达类slam论文LOAM: Lidar Odometry and Mapping in Real-time

LOAM: Lidar Odometry and Mapping in Real-time

Ji Zhang and Sanjiv Singh

摘要

我们提出了一种实时测距和建图的方法，该方法使用了以6自由度移动的2轴激光雷达的距离测量值。该问题之所以棘手，是因为在不同的时间接收到距离测量值，并且运动估计中的错误可能导致结果点云的配准错误。迄今为止，可以通过离线批处理方法来构建连贯的3D地图，通常使用闭环来校正随时间的漂移。我们的方法可实现低漂移和低计算复杂度，而无需高精度测距或惯性测量。获得这种性能水平的关键思想是同时定位和建图这一复杂问题的划分，该问题试图通过两种算法来同时优化大量变量。一种算法以高频率但低保真度执行里程测量以估计速度激光雷达。 另一个算法以较低的数量级频率运行，以进行点云的精确匹配和配准。 两种算法的组合使该方法可以实时建图。该方法已通过大量实验以及在KITTI里程表基准上进行了评估。结果表明，该方法可以在最先进的离线批处理方法水平上实现准确性。

1、绪论

3D建图仍然是一种流行的技术[1]–[3]。激光雷达的建图是很常见的，因为激光雷达可以提供高频范围的测量，而无论测得的距离如何，误差都相对恒定。在激光雷达的唯一运动是旋转激光束的情况下，点云的对准很简单。但是，如果激光雷达本身像许多感兴趣的应用一样在移动，则精确的建图需要了解连续激光测距期间的激光雷达姿态。解决该问题的一种常用方法是使用独立的位置估计（例如，通过GPS / INS）将激光点配准到固定坐标系中。另一组方法使用测距法测量，例如来自车轮编码器或视觉测距系统[4]，[5]的测距记录激光点。由于里程表会随着时间的推移整合较小的增量运动，因此它势必会漂移，并且会特别注意减少漂移（例如使用闭环）。

在这里，我们考虑了使用以6自由度移动的2轴激光雷达以低漂移测距法创建地图的情况。 使用激光雷达的主要优点是它对环境光线和场景中的光学纹理不敏感。激光雷达的最新发展减少了其尺寸和重量。 激光雷达可以由穿越环境[6]的人握住，甚至可以安装在微型飞行器[7]上。 由于我们的方法旨在解决里程表估算中与最小化漂移有关的问题，因此目前不涉及循环闭环。

该方法可实现低漂移和低计算复杂度，而无需高精度测距或惯性测量。获得这种性能水平的关键思想是同时定位和映射（SLAM）[8]这个典型的复杂问题的划分，该问题试图通过两种算法来同时优化大量变量。一种算法以高频率但低保真度执行测距法以估计激光雷达的速度。另一种算法以较低的数量级频率运行，以进行点云的精确匹配和配准。尽管没有必要，但如果有IMU，则可以提供运动先验来帮助解决高频运动问题。提取位于尖锐边缘和平面上的点，并分别将特征点与边缘线段和平面贴片匹配。在测距算法中，通过确保快速计算来找到特征点的对应关系。在建图算法中，通过关联的特征值和特征向量，通过检查局部点簇的几何分布来确定对应关系。

通过分解原始问题，更容易解决的问题是在线运动估计。 之后，将建图作为批处理优化（类似于迭代最近点（ICP）方法[9]）进行操作，以生成高精度的运动估计和制度。 并行算法结构确保了实时解决问题的可行性。 此外，由于运动估计是在较高的频率下进行的，因此建图有足够的时间来提高精度。当以较低的频率运行时，该建图算法能够合并大量特征点并使用足够多的迭代来收敛。

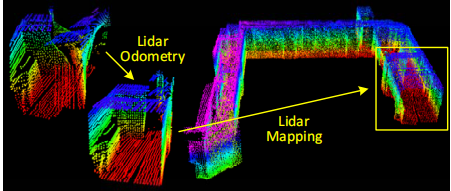
图1 该方法旨在使用运动的2轴激光雷达进行运动估计和建图。由于在不同时间接收激光点，由于激光雷达的运动（在左激光雷达云中显示），在点云中会出现畸变。 我们提出的方法通过并行运行的两种算法来分解问题。里程计算法估计激光雷达的速度并校正点云中的变形，然后，建图算法会匹配并注册点云以创建地图。两种算法的结合确保了实时解决问题的可行性

2、相关的工作

激光雷达已经成为机器人导航中一种有用的距离传感器[10]。对于定位和建图，大多数应用程序使用2D lidars [11]。当激光雷达扫描速度高于其外在运动时，扫描内的运动失真可忽略不计。在这种情况下，可以使用标准ICP方法[12]来匹配不同扫描之间的激光回波。此外，还提出了一种两步方法来消除失真[13]：基于ICP的速度估计步骤之后会出现失真补偿步骤，使用计算出的速度。类似的技术也用于补偿单轴3D激光雷达[14]引起的失真。但是，==如果扫描运动相对较慢，则运动失真可能会很严重。当使用2轴激光雷达时，尤其如此，因为一个轴通常比另一轴慢得多。==通常，其他传感器可用于提供速度测量值，从而可以消除失真。例如，激光雷达云可以通过状态估计从与IMU集成的视觉测距法中配准[15]。当同时使用多个传感器（例如GPS / INS和车轮编码器）时，通常可以通过扩展的Kalman过滤器[16]或粒子过滤器[1]解决问题。这些方法可以实时创建地图，以帮助机器人导航中的路径规划和避免碰撞。

如果在没有其他传感器帮助的情况下使用2轴激光雷达，则运动估计和失真校正将成为一个问题。 Barfoot等人使用的一种方法。通过激光强度返回创建视觉图像，并在图像之间匹配视觉上明显的特征[17]，以恢复地面车辆的运动[18]-[21]。在[18]，[19]中将车辆运动建模为恒定速度，在[20]，[21]中将模型建模为高斯过程。我们的方法使用与里程计算法中的[18]，[19]类似的线性运动模型，但具有不同类型的特征。方法[18] – [21]涉及强度图像的视觉特征，并且需要密集的点云。我们的方法提取并匹配笛卡尔空间中的几何特征，并且对云密度的要求较低。

最接近我们的方法是Bosse和Zlot [3]，[6]，[22]。他们使用2轴激光雷达获得点云，该点云通过匹配局部点簇的几何结构进行配准[22]。此外，他们使用多个2轴激光雷达来映射地下矿山[3]。此方法合并了IMU，并使用闭环来创建大型地图。 Zebedee由同一作者提出，是一种测绘装置，由2D激光雷达和通过弹簧连接到手杆的IMU组成[6]。建图是通过手动点按设备进行的。通过批处理优化方法来恢复轨迹，该批处理方法可处理在分段之间添加边界约束的分段数据集。在这种方法中，IMU的测量值用于记录激光点，而最优化则用于校正IMU偏差。本质上，Bosse and Zlot的方法需要批处理才能开发出精确的地图，因此不适用于需要实时地图的应用程序。相比之下，所提出的方法实时生成的地图与Bosse和Zlot的地图在质量上相似。区别在于我们的方法可以为自动驾驶汽车的导航提供运动估计。此外，该方法利用了激光雷达扫描图案和点云分布。在确保了里程计和建图算法中的计算速度和准确性前提下实现了特征匹配。

3、注释和任务说明

本文解决的问题是利用3D激光雷达感知到的点云执行自我运动估计，并为遍历的环境构建地图。 我们假设激光雷达已预先校准。 我们还假设，激光雷达的角速度和线性速度随时间推移是平滑且连续的，没有突变。 在第七节中，将通过使用IMU提出第二个假设。
作为本文的约定，我们使用右大写字母表示坐标系。我们将激光雷达完成一次扫描覆盖范围定义为进行一次扫描。我们使用k，k∈ $Z^{+}$表示扫描，而$P_i$ 表示在扫描k期间感知到的点云。让我们定义两个坐标系如下。

• 激光雷达坐标系{L}是3D坐标系，其原点位于激光雷达的几何中心。x轴指向左侧，y轴指向上方，z轴指向前方。 {$L_k$}中点i，i∈$P_k$的坐标表示为$X_{（k，i）}^L$。
• 世界坐标系{W}是在初始位置与{L}一致的3D坐标系。 {$W_k$}中点i，i∈$P_k$的坐标为$X_{（k，i）}^W$。

有了假设和符号，我们的激光雷达里程表和建图问题可以定义为
问题：给定一个激光雷达点云$P_k$，k∈$Z^{+}$的序列，计算每次扫掠k期间激光雷达的自我运动，并用$P_k$为遍历环境建立一个地图。

4、系统总览

A、激光雷达硬件

图2 本研究中使用的3D激光雷达由一台由电机驱动以进行旋转运动的Hokuyo激光扫描仪和一个测量旋转角度的编码器组成。

本文的研究对基于Hokuyo UTM-30LX激光扫描仪的定制3D激光雷达进行了验证，但不仅仅是验证。通过本文，我们将使用从激光雷达收集的数据来说明该方法。激光扫描仪的视场为180°，其分辨率为0.25°分辨率以及40线/秒的扫描速率。激光扫描仪连接到电机，该电机被控制为在-90度到90度之间以180°/ s的角速度旋转并且激光扫描仪的水平方向为零。对于这个特定的单元，扫描是从-90° 至90° 开始的旋转或反向旋转（持续1s）。在此，请注意，对于连续旋转的激光雷达，扫掠只是一个半球形的旋转。车载编码器以0.25°的分辨率测量电动机的旋转角度，通过此过程，激光点被投影到激光雷达坐标{L}中。

B.软件系统概述

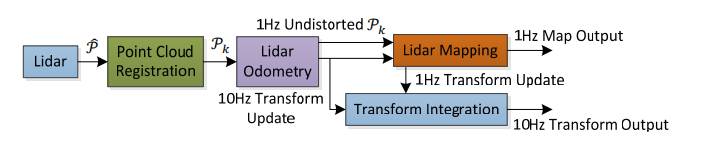
图3 激光雷达测距和制图软件系统的框图。

图3示出了软件系统的图。 让$\hat{P}$是激光扫描中收到的点。在每次扫描中，已在{L}中注册。 扫掠k期间的组合点云形成$P_k$。然后，用两种算法处理$P_k$。激光雷达测距仪获取点云，并计算两次连续扫描之间的激光雷达运动。估计的运动用于校正$P_k$中的失真。该算法以大约10Hz的频率运行。 输出由激光雷达建图进一步处理，该激光雷达建图将未失真的云匹配并以1Hz的频率记录到地图上。 最后，将两种算法发布的姿态变换集成在一起，以生成相对于地图的激光雷达姿态约为10Hz的变换输出。 第五节和第六节详细介绍了软件图中的方框。

5、激光雷达

A.特征点提取

我们首先从激光雷达云$P_k$中提取特征点。图2所示的激光雷达会在$P_k$中自然地生成不均匀分布的点。激光扫描仪在一次扫描中的返回分辨率为0.25°。这些点位于扫描平面上。 但是，由于激光扫描仪以180°/ s的角速度旋转并以40Hz的频率进行扫描，垂直于扫描平面的分辨率为180°/ 40 = 4.5°。 考虑到这一事实，仅使用来自各个扫描的信息以及共面几何关系从$P_k$中提取特征点。
我们选择位于尖锐边缘和平面贴片上的特征点。设i为$P_k$中的一个点，i∈$P_k$，设S为同一扫描中激光扫描仪返回的i的连续点的集合。 由于激光扫描仪会按CW或CCW顺序生成返回点，因此S在i的两边分别包含一半的点并且两点之间有和0.25°的间隔。定义一个术语来评估局部表面的光滑度
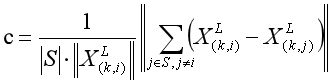$$(1)$$
扫描中的点基于c值进行排序，然后选择特征点，其特征是最大c（即边缘点）和最小c（即平面点）。 为了在环境中均匀分布特征点，我们将扫描分为四个相同的子区域。 每个子区域最多可以提供2个边缘点和4个平面点。 仅当点i的c值大于或小于阈值且所选点的数量不超过最大值时，才可以将其选择为边或平面点。

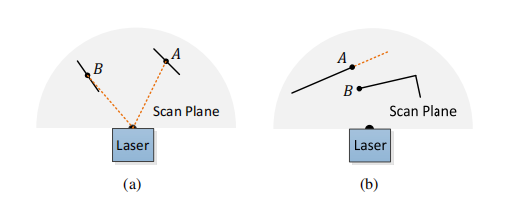
图4 （a）实线段代表局部表面斑块。 点A位于与激光束成一定角度（橙色虚线段）的表面贴片上。 点B位于大致平行于激光束的表面斑片上。 我们将B视为不可靠的激光返回，因此请勿将其选择为特征点。 （b）实线段是激光的可观察对象。点A在遮挡区域（橙色虚线段）的边界上，可以检测为边缘点。 但是，如果从不同角度观看，则遮挡区域可能会发生变化并变得可观察。 我们不会将A视为显着的边缘点，也不会将其选择为特征点。

在选择特征点时，要避免选择已选择的特征点周围的点或局部平行于激光束的局部平面上的点，这些点通常被认为是不可靠的，如图4（a）所示，其中（a）中实线段代表局部表面斑块，点A位于与激光束成一定角度（橙色虚线段）的表面上，点B位于大致平行于激光束的表面上，这种情况下将B视为不可靠的激光返回点，因此勿将其选择为特征点。此外，我们要避免选择遮挡区域边界上的点[23]，如图4（b）所示，其中（b）实线段是激光的可观察对象，点A在遮挡区域（橙色虚线段）的边界上，会被检测为边缘点。但是，如果从不同角度观看，则遮挡区域可能会变得可观察，因此不会将A视为突出边缘点，也不会将其选择为特征点。

如果选择了一个点，当点云集S形成的平面大致不平行于激光束，且在S中没有点在激光束方向上与i通过一个间隙断开并且同时比点i更靠近激光雷达，如图4（b）中的点B，这样提取出来的点才能成为特征点。

图5 从走廊中拍摄的激光雷达云中提取的边缘点（黄色）和平面点（红色）的示例。 同时，激光雷达以0.5m / s的速度朝向图左侧的墙壁移动，这导致墙壁上的运动变形。

从走廊场景中提取的特征点的示例如图5所示。边缘点和平面点分别用黄色和红色标记。

综上所述，选择特征点的标准是：

• 从最大c值开始选择特征点作为边缘点，从最小c值开始选择平面点。
• 所选边缘点或平面点的数量不能超过子区域的最大值。
• 其周围的点尚未被选为特征点。
• 不能在与激光束大致平行的表面上，也不能在被遮挡区域的边界上。

B.寻找特征点对应点

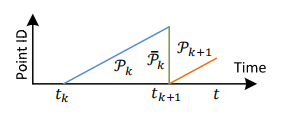
图6 将点云重新投影到扫描结束。 蓝色的线段表示在扫描k期间感知到的点云 $P_k$。 在扫描k结束时，将$P_k$重新投影到时间戳$t_{k+1}$，以获得$\overline{P_k}$（绿色线段）。 然后，在扫描k + 1期间，$\overline{P_k}$和新感知的点云$P_{k+1}$（橙色线段）一起用于估计激光雷达运动。

测距算法估计扫描中激光雷达的运动。令$t_k$为扫频k的开始时间。 在每次扫描结束时，在扫描过程中感知到的点云$P_k$，将重新投影到时间戳$t_{k+1}$，如图6所示。我们将重新投影的点云表示为$\overline{P_k}$。 在下一个扫描k + 1期间，$\overline{P_k}$与新接收的点云$P_{k+1}$一起用于估计激光雷达的运动。
让我们假设$\overline{P_k}$和$P_{k+1}$现在都可用，并从找到两个激光雷达云之间的对应关系开始。 对于$P_{k+1}$，我们使用上一部分中讨论的方法从激光雷达云中找到边缘点和平面点。 令${\xi }_{k+1}$和$H_{k+1}$分别为边缘点和平面点的集合。 我们将发现$\overline{P_k}$中的边线是${\xi }_{k+1}$中点的对应，而平面块是$H_{k+1}$中点的对应。

在扫描k + 1的开始处，$P_{k+1}$是一个空集，随着接收到更多的点，在扫描过程中$P_{k+1}$会增加。激光雷达里程表递归估计扫描期间的6自由度运动，并随着$P_{k+1}$的增加逐渐包含更多点。在每次迭代中，使用当前估计的变换将${\xi }_{k+1}$重新投影到扫描的开始，令${\tilde{\xi }}_{k+1}$为重投影点集，$H_{k+1}$同理得到${\tilde{H}}_{k+1}$，对于${\tilde{\xi }}_{k+1}$和${\tilde{H}}_{k+1}$中的每个点，在$\overline{P_k}$中找到最接近的邻点。此处，$\overline{P_k}$存储在3D KD树[24]中以进行快速索引。

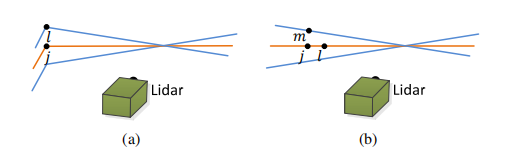
图7 找到一条边线作为${\tilde{\xi }}_{k+1}$（a）中的一个边缘点的对应关系，找到一个平面块作为${\tilde{H}}_{k+1}$（b）中的一个平面点的对应关系。 在（a）和（b），j是在$\overline{P_k}$中找到的最接近特征点的点。 橙色线代表对j的相同扫描，蓝色线代表两个连续的扫描。 为了在（a）中找到边线对应关系，我们在蓝色线上找到另一个点l，并将对应关系表示为（j，l）。 为了在（b）中找到平面补丁对应关系，我们分别在橙色和蓝色线上找到另外两个点l和m，对应关系为（j，l，m）

图7（a）表示找到边缘线作为边缘点的对应关系的过程。 令i成为${\tilde{\xi }}_{k+1}$中的一个点，i∈${\tilde{\xi }}_{k+1}$。 边缘线由两点表示。 令j为$\overline{P_k}$中i的最近邻点，j∈$\overline{P_k}$，令l为到j的两次连续扫描中i的最近邻点。 （j，l）形成i的对应关系。 然后，为了验证j和l都是边缘点，我们基于公式（1）检查局部表面的光滑度。 在此，我们特别要求j和l来自不同的扫描，考虑到一次扫描不能包含一个以上的来自同一边缘线的点。但在扫描平面上是一个例外。 但是，如果是这样，则边缘线将退化并在扫描平面上显示为直线，并且边缘线的特征点不应首先提取。

图7（b）表示找到一个平面块作为一个平面点的对应关系的过程。设i是${\tilde{H}}_{k+1}$，i∈${\tilde{H}}_{k+1}$的一个点。平面斑块由三个点表示。在$\overline{P_k}$中找到i的最近邻点，表示为j。然后，分别在橙色和蓝色线上找到另外两个点l和m，对应关系为（j，l，m），它们是i的最近邻点，一个点在与j相同的扫描中，另一个在到j的扫描的两次连续扫描中。这保证了这三个点是非共线的。为了验证j，l和m均为平面点，我们基于公式 (1)再次检查局部表面的光滑度。

利用找到的特征点的对应关系，导出表达式以计算从特征点到其对应量的距离并将通过使特征点的总距离最小化来恢复激光雷达运动。 首先从边缘点开始。

对于点i∈${\tilde{\xi }}_{k+1}$，如果（j，l）是相应的边线j，l∈$\overline{P_k}$，则点到线的距离可以算为

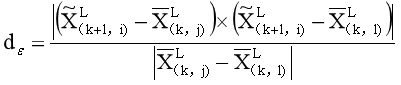
$$(2)$$
其中，${\tilde{X}}_{（k+1，i）}^L$，${\bar{X}}_{（k，j）}^L$，${\bar{X}}_{（k，l）}^L$分别是i,j，l在{L}坐标系里的坐标。那么，对于点i∈${\tilde{H}}_{k+1}$，如果（j，l，m）是对应的平面块，j，l，m∈$\overline{P_k}$，则点到平面的距离为

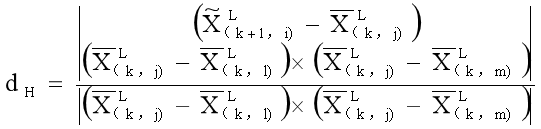
$$(3)$$

其中${\bar{X}}_{（k，m）}^L$是m点在{L}坐标系里的坐标。

C.运动估计

在扫描过程中以恒定的角速度和线速度对激光雷达运动进行建模，可以在扫描中对不同时间接收的点进行线性内插姿态变换。
令t为当前时间戳，$t_{k+1}$是扫描k+1次的开始时间。$T_{k+1}^L$=${\left[\begin{array}{cccccc}{t}_x& t_y& t_z& {\theta }_x& {\theta }_y& {\theta }_z\end{array}\right]}^T$，其中前三个参数分别是在{L}坐标系中沿着x-, y-,z-轴的平移量，后三个参数是遵循右手定律的旋转角。给定点i，i∈$P_{k+1}$，令$t_i$为其时间戳，$T_{(k+1,i)}^L$为[$t_{k+1}$，$t_i$]之间的姿态变换。$T_{(k+1,i)}^L$可以通过$T_{k+1}^L$的线性插值来计算

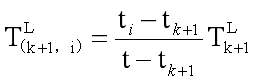
$$(4)$$
${\xi }_{k+1}$ 和$H_{k+1}$是从$P_{k+1}$提取的边缘点和平面点的集合，而${\tilde{\xi }}_{k+1}$和${\tilde{H}}_{k+1}$是重新投影到扫描开始$t_{k+1}$的点的集合。为了解决激光雷达运动，需要在${\xi }_{k+1}$ 和${\tilde{\xi }}_{k+1}$或$H_{k+1}$和${\tilde{H}}_{k+1}$之间建立几何关系。使用（4）中的变换，可以得出

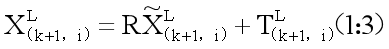
$$(5)$$

其中$X_{（k+1，i）}^L$是${\xi }_{k+1}$ 或者$H_{k+1}$中点i的坐标，${\tilde{X}}_{（k+1，i）}^L$是${\tilde{\xi }}_{k+1}$或者${\tilde{H}}_{k+1}$中对应点的坐标，$T_{(k+1,i)}^L$(a:b)是$T_{(k+1,i)}^L$的第a至b个条目，R为由罗德里格斯公式[25]定义的旋转矩阵

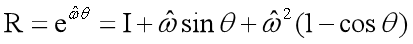
$$(6)$$
其中，$\theta$是旋转的大小

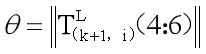
$$(7)$$

ω是代表旋转方向的单位向量

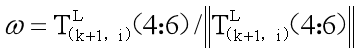
$$(8)$$
其中，$\hat{\omega }$是$\omega$的斜对称矩阵[25]。

以上公式中，（2）和（3）计算${\tilde{\xi }}_{k+1}$和${\tilde{H}}_{k+1}$中的点之间的距离及其对应关系。 结合（2）和（4）-（8）的公式，可以得出${\xi }_{k+1}$中的边缘点和相应的边缘线之间的几何关系

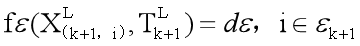
$$(9)$$
类似地，结合（3）和（4）-（8），可以在$H_{k+1}$中的一个平面点和对应的平面块之间建立另一个几何关系

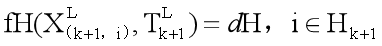
$$(10)$$
最后，用Levenberg-Marquardt方法[26]解决激光雷达的运动。对于${\xi }_{k+1}$和$H_{k+1}$中的每个特征点堆叠（9）和（10），得到一个非线性函数

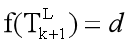
$$(11)$$
其中f的每一行都对应一个特征点，而d包含相应的距离。计算相对于$T_{k+1}^L$的f的雅可比矩阵，记为J，其中J=$\frac{\partial f}{\partial T_{k+1}^L}$。然后，可以通过将d最小化为零，非线性迭代来求解（11）

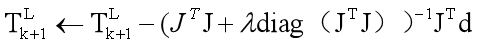
$$(12)$$

λ是通过Levenberg-Marquardt方法确定的因子。

D、激光雷达里程计算法

激光雷达测距算法将最后一次扫描的点云$\overline{P_k}$，当前扫描的点云$P_{k+1}$和最后一次递归的姿态变换$T_{k+1}^L$作为输入。如果开始新的扫描，则$T_{k+1}^L$设置为零。然后，该算法从$P_{k+1}$中提取特征点来构造${\xi }_{k+1}$和$H_{k+1}$。对于每个特征点，在$\overline{P_k}$中找到它们的对应关系。运动估计适应鲁棒拟合[27]，算法为每个特征点分配双平方权重：与它们的对应关系具有较大距离的特征点被分配较小的权重，而距离大于阈值的特征点被视为异常值并被分配零权重。然后，将姿态转换在一次迭代中进行更新。如果找到收敛或达到最大迭代次数，则非线性优化将终止。如果算法到达扫描结束，则使用扫描期间的运动估计将$P_{k+1}$重新投影到时间戳$t_{k+2}$。否则，仅返回变换$T_{k+1}^L$进行下一轮递归。

6、建图算法

在每次扫描中，建图算法只调用一次，且其运行频率比里程计算法低。在扫描k + 1结束时，里程表会获得未失真的点云${\bar{P}}_{k+1}$，以及姿势变换$T_{k+1}^L$，包含扫描在[$t_{k+1}$，$t_{k+2}$]期间的激光雷达运动。建图算法在世界坐标{W}中匹配${\bar{P}}_{k+1}$，如图8所示，蓝色曲线表示在扫描k时由建图算法生成的地图上的激光雷达姿态$T_k^W$，橙色曲线表示由测距算法计算的扫描k + 1，$T_{k+1}^L$期间的激光雷达运动。利用激光雷达测距仪的输出，对于$T_k^W$和$T_{k+1}^L$，建图算法将$T_k^W$扩展为从$t_{k+1}$到$t_{k+2}$的一次扫描，以获得$T_{k+1}^W$，并将${\bar{P}}_{k+1}$投影到世界坐标{W}中，即将由测距算法发布的未失真点云投影到地图上，表示为${\bar{Q}}_{k+1}$，在图中用绿色线段表示。接下来，算法通过优化激光雷达姿态$T_{k+1}^W$将${\bar{Q}}_{k+1}$与地图上现有的点云$Q_k$匹配，$Q_k$用黑色线段表示。

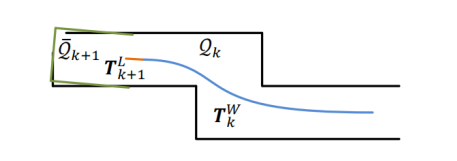
图8

提取特征点的方式与5-A节相同，但提取的特征点数量是之前的10倍。为了找到特征点的对应量，首先，将地图$Q_k$上的点云存储在边长为10m的立方体区域中，提取立方体中与${\bar{Q}}_{k+1}$相交的点，存储在三维KD树中[25]。令S’为一组在特征点周围的某个区域内找到的$Q_k$中的周围点，对于边缘点，仅将点保留在S’中的边缘线上，对于平面点，仅将点保留在平面块上。然后，计算S’的协方差矩阵，记为M，M的特征值和特征向量分别记为V和E。如果S’分布在边缘线上，则V包含一个特征值，该特征值明显大于其他两个特征值，并且E中与最大特征值相关的特征向量表示边缘线的方向。另一方面，如果将S’分布在平面块上，则V包含两个较大的特征值，而第三个特征值则明显更小，并且E中与最小特征值相关的特征向量表示平面块的方向。边缘线或平面块的位置通过穿过S’的几何中心来确定。

在边线上选择两个点，在平面块上选择三个点，就可以使用（2）和（3）的公式来计算从特征点到其对应点的距离。接下来，为每个特征点列出一个（9）或（10）的等式，但不同之处在于${\bar{Q}}_{k+1}$中的每一个数据点的时间戳$t_{k+2}$都是一样的。通过Levenberg-Marquardt方法[27]的鲁棒拟合[28]再次求解非线性优化问题，并且将${\bar{Q}}_{k+1}$进行配准，为了使点均匀分布，设置了体素网格过滤器[29]，来缩小地图中点云的体量。
姿态变换的积分如图9所示。每扫描一次，从激光雷达地图输出的位姿$T_k^W$用蓝色区域表示，橙色区域表示以10Hz左右的频率从激光雷达测距法输出的变换$T_{k+1}^L$，两个变换$T_k^W$和$T_{k+1}^L$的组合就是激光雷达相对于地图的姿态，其频率与激光雷达里程计的频率相同。

图9

7、实验

在实验过程中，处理激光雷达数据的算法在具有2.5GHz四核和6Gib内存的便携式计算机上的Linux机器人操作系统（ROS）上运行[29]。该方法总共消耗两个内核，里程计和建图程序在两个单独的内核上运行。我们的软件代码和数据集可公开获得1,2。

A、室内和室外测试集

该方法已在室内和室外环境中进行了测试。在室内测试期间，激光雷达与电池和便携式计算机一起放在推车上。一个人推着推车走。图10（a）和图10（c）显示了在两个代表性的室内环境（狭窄而又长的走廊和宽敞的大厅）中构建的地图。图10（b）和图10（d）示出了从相同场景拍摄的两张照片。在室外测试中，激光雷达安装在地面车辆的前部。 图10（e）和图10（g）示出了从两排树之间的植被道路和果园生成的地图，并且照片分别在图10（f）和图10（h）中呈现。 在所有测试期间，激光雷达以0.5m / s的速度移动。

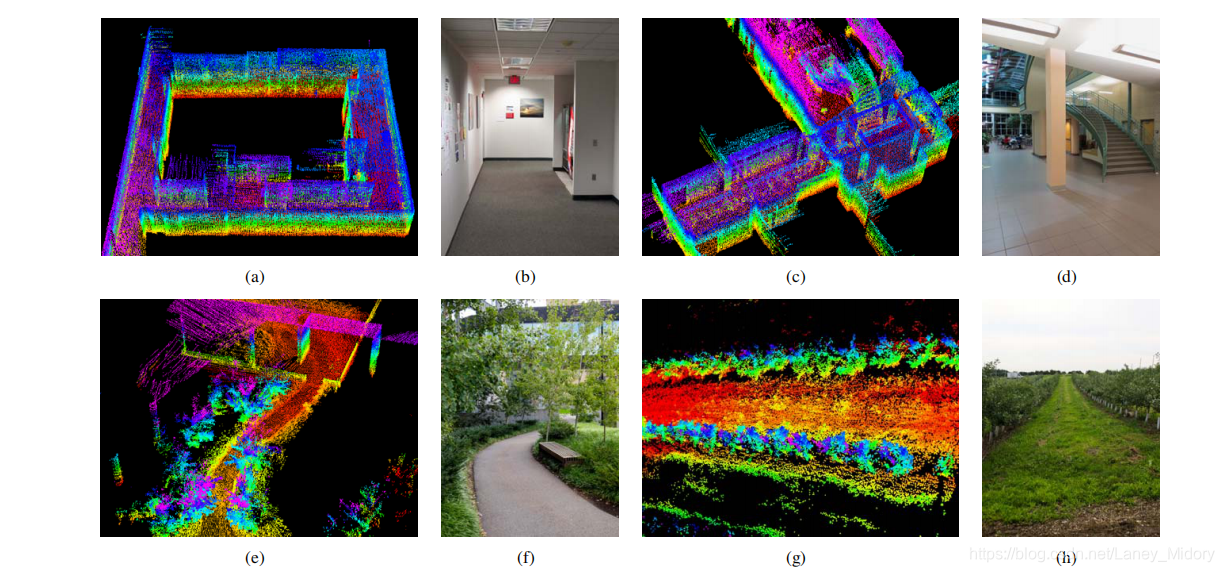
图10 （a）-（b）狭窄又长的走廊，（c）-（d）大厅，（e）-（f）植被道路和（g）-（h）在两排树之间的果园。 在室内测试中，将激光雷达放置在推车上，在室外测试中，将激光雷达安装在地面车辆上。 所有测试均使用0.5m / s的速度。

为了评估地图的局部准确性，我们从相同的环境中收集了第二组激光雷达云。 激光雷达保持静止，并在数据选择期间将其放置在每种环境中的几个不同位置。两点云通过点对面ICP方法进行匹配和比较[9]。匹配完成后，将一个点云与第二个点云中相应的平面块之间的距离视为匹配误差。 图11示出了误差分布的密度。与室外相比，它表明室内环境的匹配误差较小。结果是合理的，因为自然环境中的特征匹配不如人工环境中的精确。

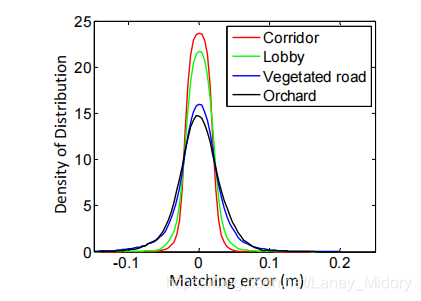
图11 走廊（红色），大厅（绿色），植被道路（蓝色）和果园（黑色）的匹配误差，对应于图10中的四个场景

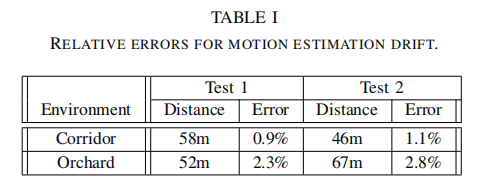
此外，我们进行测试以测量运动估计值的累积漂移。我们选择包含闭环的室内走廊来实验。这使我们可以在同一位置开始和结束。运动估计会在开始位置和结束位置之间生成间隙，该间隙指示漂移量。对于户外实验，我们选择果园环境。 搭载激光雷达的地面车辆配备了用于地面真相采集的高精度GPS / INS。将测得的漂移与作为相对精度的行进距离进行比较，并列在表I中。具体地说，测试1使用与图10（a）和图10（g）相同的数据集。通常，室内测试的相对精度约为1％，而室外测试的精度约为2.5％。

B、IMU的帮助

我们将Xsens MTi-10 IMU连接到激光雷达，以应对快速的速度变化。 点云经过两种方式进行预处理，然后再发送到所提出的方法中：1）从IMU确定方向，旋转一次扫描接收的点云以使其与该扫描中激光雷达的初始方向对齐； 2）进行加速度测量 ，运动失真将部分消除，就像激光雷达在扫掠期间以恒定速度移动一样。 然后由激光雷达测距仪和制图程序处理点云。

通过将来自陀螺仪的角速率和来自加速度计的读数在卡尔曼滤波器中[1]积分，可以得到IMU的方向。 图12（a）示出了样本结果。 一个人拿着激光雷达，在楼梯上行走。 在计算红色曲线时，我们使用IMU提供的方向，而我们的方法仅估算平移。 在5分钟的数据收集期间方向偏移超过25° 。 假设没有IMU可用，绿色曲线仅取决于我们方法中的优化。 蓝色曲线使用IMU数据进行预处理，然后再使用提出的方法。 我们观察到绿色和蓝色曲线之间的微小差异。 图12（b）显示了对应于蓝色曲线的图。 在图12（c）中，我们比较了图12（b）中黄色矩形中的两个闭合视图。 上图和下图分别对应于蓝色和绿色曲线。 仔细比较发现，上图中的边缘较锐利。

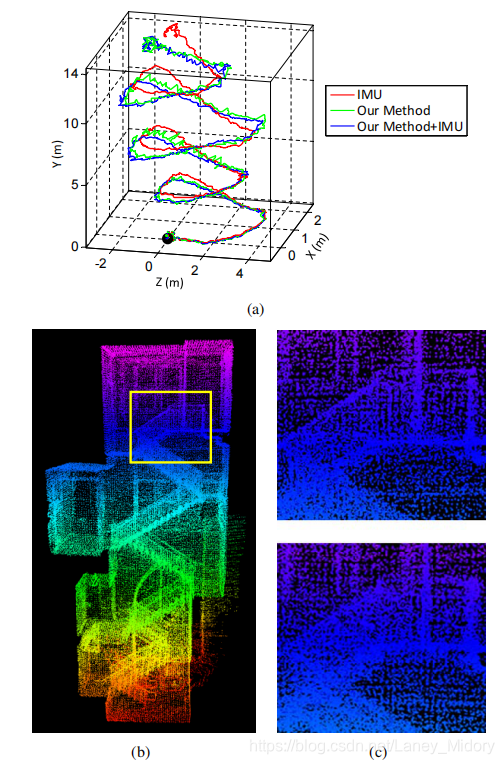
图12 使用/不使用IMU的结果比较。 一个人拿着激光雷达，在楼梯上行走。 黑点是起点。 在（a）中，红色曲线是使用IMU的方向和通过我们的方法估算的平移计算的，绿色曲线仅依赖于我们方法中的优化，蓝色曲线使用IMU数据进行预处理，然后使用该方法。 （b）是对应于蓝色曲线的图。 在（c）中，使用（b）中以黄色矩形标记的区域，上图和下图分别对应于蓝色和绿色曲线。 上图中的边缘更锐利，表明地图上的准确性更高。

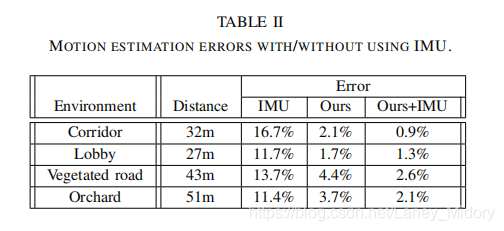
表II比较了使用和不使用IMU的运动估计中的相对误差。 激光雷达由一个以0.5m / s的速度行走并以0.5m左右的幅度上下移动激光雷达的人握住。 地面真相由卷尺手动测量。 在所有四个测试中，在IMU的协助下使用我们提出的方法可提供最高的精度，而仅使用来自IMU的方向只能导致最低的精度。 结果表明，IMU可以有效地消除非线性运动，从而解决了线性运动问题。

C、KITTI数据集实验

我们还使用来自KITTI里程表基准测试[30]，[31]的数据集评估了我们的方法。 使用安装在结构化道路上的乘用车顶部的传感器（图13（a））对数据集进行充分配准。 该车配备了360°Velodyne激光雷达，彩色/单色立体相机和用于采集ground truth的高精度GPS / INS。 激光雷达数据以10Hz记录，并由我们的里程计估计方法使用。由于篇幅所限，我们无法包含结果 但是，我们鼓励读者在基准网站上查看我们的结果3。

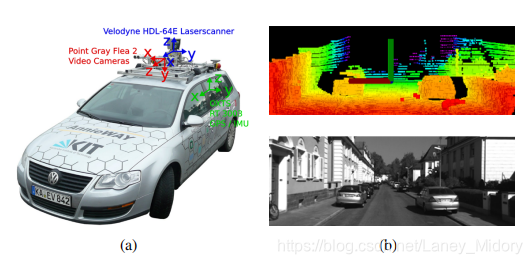
图13 （a）KITTI基准测试所使用的传感器配置和车辆。该车辆安装了Velodyne激光雷达，立体摄像头和用于地面真相采集的高精度GPS / INS。 我们的方法仅使用Velodyne激光雷达的数据。 （b）样本激光雷达云（上图）和来自城市场景的相应视觉图像（下图）。

数据集主要涵盖三种类型的环境：周围有建筑物的“城市”，有植被的小路上的“乡村”和道路宽阔的“高速公路”且周围环境相对整洁。图13（b）显示了一个样本激光雷达云和来自城市环境的相应视觉图像。数据集中包括的总行驶距离为39.2公里。在上传车辆轨迹时，基准服务器会自动计算准确性和排名。 在通过基准测试评估的所有方法中，这些方法与感测模态无关，包括最新的立体视觉测距法[32]，[33]，我们的方法均排名第一。 在3D坐标中使用100m，200m，…，800m长度的轨迹段生成的平均位置误差为行进距离的0.88％。

8、结论与未来工作

使用来自旋转激光扫描仪的点云进行运动估计和制图可能很困难，因为在激光雷达云中大量运动恢复和运动失真校正方面存在问题。所提出的方法通过并行运行的两种算法来解决该问题：激光雷达测距法可进行粗略处理以估计较高频率的速度，而激光雷达建图可进行精细处理以创建较低频率的地图。两种算法的配合可实现精确的运动估计和实时映射。此外，该方法可以利用激光雷达扫描图案和点云分布进行特征匹配以确保里程计算法中的快速计算，并增强建图算法中的准确性。该方法已在室内和室外以及KITTI里程表基准上进行了测试。由于当前方法无法识别回路闭合，因此我们未来的工作涉及开发一种通过闭合回路来修正运动估计漂移的方法。同样，我们将把我们的方法的输出与卡尔曼滤波器中的IMU集成在一起，以进一步减少运动估计漂移。

推荐几篇好的博客共同学习：

LOAM笔记及A-LOAM源码阅读
LOAM论文与代码解析
对于前半部分的理解以及一些图很不错，但是有些小错误：点这里
LOAM源码解析
LOAM细节分析
LOAM, ALOAM, LegoLOAM, hdl graph slam比较
ALOAM试跑及程序注释

参考文献

REFERENCES
[1] S. Thrun, W. Burgard, and D. Fox, Probabilistic Robotics. Cambridge,MA, The MIT Press, 2005.
[2] M. Kaess, H. Johannsson, R. Roberts, V. Ila, J. Leonard, and F. Dellaert,“iSAM2: Incremental smoothing and mapping using the bayes tree,” The International Journal of Robotics Research, vol. 31, pp. 217–236, 2012.
[3] R. Zlot and M. Bosse, “Efficient large-scale 3D mobile mapping and surface reconstruction of an underground mine,” in The 7th International Conference on Field and Service Robots, Matsushima, Japan, July 2012.
[4] K. Konolige, M. Agrawal, and J. Sol, “Large-scale visual odometry for rough terrain,” Robotics Research, vol. 66, p. 201212, 2011.
[5] D. Nister, O. Naroditsky, and J. Bergen, “Visual odometry for ground vechicle applications,” Journal of Field Robotics, vol. 23, no. 1, pp.3–20, 2006.
[6] M. Bosse, R. Zlot, and P. Flick, “Zebedee: Design of a spring-mounted 3-D range sensor with application to mobile mapping,” vol. 28, no. 5,pp. 1104–1119, 2012.
[7] S. Shen and N. Michael, “State estimation for indoor and outdoor operation with a micro-aerial vehicle,” in International Symposium on Experimental Robotics (ISER), Quebec City, Canada, June 2012.
[8] H. Durrant-Whyte and T. Bailey, “Simultaneous localization and mapping: part i the essential algorithms,” IEEE Robotics & Automation Magazine, vol. 13, no. 2, pp. 99–110, 2006.
[9] S. Rusinkiewicz and M. Levoy, “Efficient variants of the ICP algorithm,”in Third International Conference on 3D Digital Imaging and Modeling(3DIM), Quebec City, Canada, June 2001.
[10] A. Nuchter, K. Lingemann, J. Hertzberg, and H.Surmann, “6D SLAM–3D mapping outdoor environments,” Journal of Field Robotics, vol. 24,no. 8-9, pp. 699–722, 2007.
[11] S. Kohlbrecher, O. von Stryk, J. Meyer, and U. Klingauf, “A flexible and scalable SLAM system with full 3D motion estimation,” in IEEE International Symposium on Safety, Security, and Rescue Robotics,Kyoto, Japan, September 2011.
[12] F. Pomerleau, F. Colas, R. Siegwart, and S. Magnenat, “Comparing ICP variants on real-world data sets,” Autonomous Robots, vol. 34, no. 3, pp.133–148, 2013.
[13] S. Hong, H. Ko, and J. Kim, “VICP: Velocity updating iterative closest point algorithm,” in IEEE International Conference on Robotics and Automation (ICRA), Anchorage, Alaska, May 2010.
[14] F. Moosmann and C. Stiller, “Velodyne SLAM,” in IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, June 2011.
[15] S. Scherer, J. Rehder, S. Achar, H. Cover, A. Chambers, S. Nuske, and S. Singh, “River mapping from a flying robot: state estimation, river detection, and obstacle mapping,” Autonomous Robots, vol. 32, no. 5,pp. 1 – 26, May 2012.
[16] M. Montemerlo, S. Thrun, D. Koller, and B. Wegbreit, “FastSLAM: A factored solution to the simultaneous localization and mapping problem,” in The AAAI Conference on Artificial Intelligence, Edmonton, Canada,July 2002.
[17] H. Bay, A. Ess, T. Tuytelaars, and L. Gool, “SURF: Speeded up robust features,” Computer Vision and Image Understanding, vol. 110, no. 3,pp. 346–359, 2008.
[18] H. Dong and T. Barfoot, “Lighting-invariant visual odometry using lidar intensity imagery and pose interpolation,” in The 7th International Conference on Field and Service Robots, Matsushima, Japan, July 2012.
[19] S. Anderson and T. Barfoot, “RANSAC for motion-distorted 3D visual sensors,” in 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, Nov. 2013.
[20] C. H. Tong and T. Barfoot, “Gaussian process gauss-newton for 3D laserbased visual odometry,” in IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, May 2013.
[21] S. Anderson and T. Barfoot, “Towards relative continuous-time SLAM,”in IEEE International Conference on Robotics and Automation (ICRA),Karlsruhe, Germany, May 2013.
[22] M. Bosse and R. Zlot, “Continuous 3D scan-matching with a spinning 2D laser,” in IEEE International Conference on Robotics and Automation, Kobe, Japan, May 2009.
[23] Y. Li and E. Olson, “Structure tensors for general purpose LIDAR feature extraction,” in IEEE International Conference on Robotics and Automation, Shanghai, China, May 9-13 2011.
[24] M. de Berg, M. van Kreveld, M. Overmars, and O. Schwarzkopf, Computation Geometry: Algorithms and Applications, 3rd Edition. Springer,2008.
[25] R. Murray and S. Sastry, A mathematical introduction to robotic manipulation. CRC Press, 1994.
[26] R. Hartley and A. Zisserman, Multiple View Geometry in Computer Vision. New York, Cambridge University Press, 2004.
[27] R. Andersen, “Modern methods for robust regression.” Sage University Paper Series on Quantitative Applications in the Social Sciences, 2008.
[28] R. B. Rusu and S. Cousins, “3D is here: Point Cloud Library (PCL),”in IEEE International Conference on Robotics and Automation (ICRA),Shanghai, China, May 9-13 2011.
[29] M. Quigley, B. Gerkey, K. Conley, J. Faust, T. Foote, J. Leibs, E. Berger,R. Wheeler, and A. Ng, “ROS: An open-source robot operating system,”in Workshop on Open Source Software (Collocated with ICRA 2009),Kobe, Japan, May 2009.
[30] A. Geiger, P. Lenz, and R. Urtasun, “Are we ready for autonomous driving? The kitti vision benchmark suite,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2012, pp. 3354–3361.
[31] A. Geiger, P. Lenz, C. Stiller, and R. Urtasun, “Vision meets robotics:The KITTI dataset,” International Journal of Robotics Research, no. 32,pp. 1229–1235, 2013.
[32] H. Badino and T. Kanade, “A head-wearable short-baseline stereo system for the simultaneous estimation of structure and motion,” in IAPR Conference on Machine Vision Application, Nara, Japan, 2011.
[33] A. Y. H. Badino and T. Kanade, “Visual odometry by multi-frame feature integration,” in Workshop on Computer Vision for Autonomous Driving(Collocated with ICCV 2013), Sydney, Australia, 2013.