MATLAB——基于自回归积分移动平均线 （ARIMA） 模型对数据进行预测

通过1985至20222年各年的参加测试人数为实际数据，通过ARIMA模型对未来十年参加测试人数进行预测。

%clc, clear 
Y=data(:, 2);
N = length(Y);
t=1985:2022;
figure(1)
plot(t',Y); 
title('高考人数')
ylabel('万人')

 

首先，将历年测试人数增据进行可视化。可以看出，测试人数整体为上升趋势。
通过ARIMA模型进行预测。

model = arima(1,0,1);
Y0=Y(1:4);
[fit,VarCov] = estimate(model,Y,'Y0',Y0);

Y1=Y(1:19);
Y2=Y(20:end);
Yf1 = forecast(fit,19,'Y0',Y1);
figure(2)
plot(1985:2022,Y,'b','LineWidth',2)
hold on
plot(2004:2022,Yf1,'k--','LineWidth',1.5)
%xlim([1985 2022])
title('预测走势')
legend('实际值','预测值','Location','NorthWest')
hold off

通过，测试参与人数的实际走势与预测走势，对比可以看出两者总趋势都是上升的但是整体还是有一定的误差，也可以说明ARIMA模型能够在一定程度上反映其走势情况，但是，对于测试人数在现实中与整个社会的政策和形势还是有较强的相关性的。

plotForecast(Y, fit)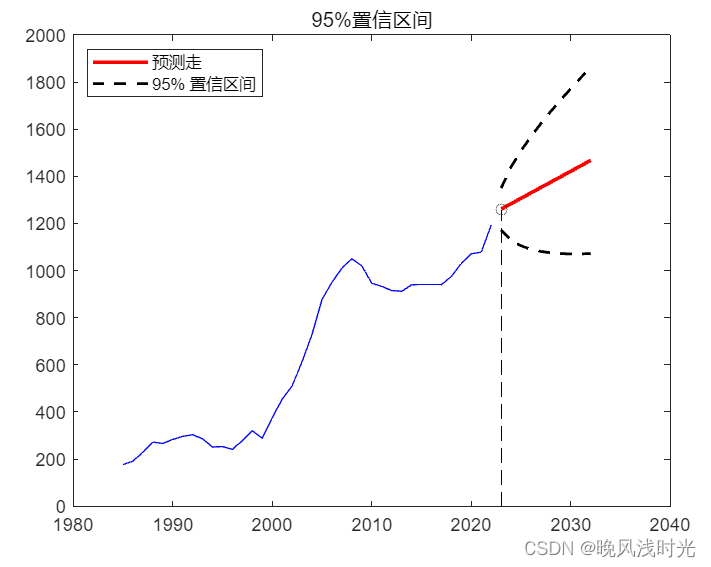

从此图中可以看出，已经训练的模型对未来测试人数预测的结果，同时还得到了人数百分之95的置信波动区间，这也显示出了未来测试人数可能波动的范围，预测的时间越长，波动的范围越大，也说明了预测时间越长，结果也不会很准确。
从整体实验可以看出，测试人数的趋势还是与社会有较强的相关性，时间序列方法可以在一定程度上反映测试人数的走势，对未来测试相关公司与职位有一定的参考意义，但是如果预测的时间较长，还是有一定的误差的。

 

表达数据的美丽：专业的Matlab图形绘制服务

       图表是数据的语言，它们能够清晰、生动地展示复杂的信息。具备熟练的Matlab技能，能够创造各种类型、风格的图表。无论是线图、柱状图、散点图、等高线图还是特殊定制的图表，调整线型、颜色、标签、图例等属性，让每个图表都符合你的品味和需求。

       如果你希望通过精美的图表展现数据的魅力，想让你的数据展示更加清晰、有吸引力，那么请联系我们（私信或加Q（1275403750））！