AcWing 245. 你能回答这些问题吗（线段树）

线段树好容易段错误啊。。干脆叫线段错误树算了！

如果想复习一下线段树，戳这：线段树蓝书讲解

题意：

思路：

本题依据题意需要进行单点修改，因此无需懒标记pushdown操作，只需要pushup操作即可。

对于查询区间内部的最大子段和，我们需要想想每个节点内部需要存储哪些信息 才能保证儿子节点向父亲节点顺利pushup传递信息（这是我们面对线段树题目时的一个很重要的思考点） 。

设线段树中的节点为“node”，我们显然最先应该存储区间的左、右端点：l、r，因为线段树本质上是一棵由区间作为节点的二叉树。

同时，依据题意还应该存区间内部的最大连续子段和，我们用total_max表示，简写为tmax。

我们来想一下，只存这些信息就够了吗？只利用当前存储的信息，能够实现 父节点的最大连续子段和tmax 由 两个儿子节点的最大连续子段和 求出吗？

显然是不够的。

原因：两个儿子节点各自tmax可能会出现完全处于区间内部的情况，且不包含边界，然而父亲节点的tmax可能会出现“横跨两个区间的情况”。就好比下图所示（红色括号所包括的范围表示节点的tmax）：

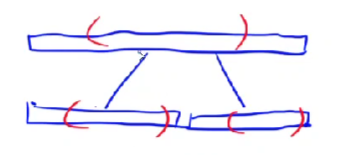
对于像上图的这种“父节点tmax横跨两个区间”的这种情况，我们其实需要再额外存储两个信息：

• ①以左儿子区间右端点为起点 向左 的最大后缀和。

• ②以右儿子区间左端点为起点 向右 的最大前缀和。

小结一下，也就是说每个节点还需要存储它的 最大前缀和 和 最大后缀和，这样， 父节点“横跨两区间”的最大连续子段和 等于 左儿子的最大后缀和 加上 右儿子的最大前缀和。

（左右儿子区间完全独立，两者没有任何关系，没有限制，左右两区间取max即为父节点tmax）

我们设节点最大前缀和为lmax，最大后缀和为rmax。

我们有下面三种情况：

父节点tmax没有横跨区间的情况包含两种：

• ①完全在左儿子区间内部：tmax = 左儿子tmax

• ②完全在右儿子区间内部：tmax = 右儿子tmax

父节点tmax横跨两区间情况为一种：

• ③tmax = 左儿子rmax + 右儿子lmax

综合一下得出表达式：

父节点u.tmax = max{L_son.tmax, R_son.tmax, L_son.rmax + R_son.lmax}

至此，我们已有方法计算出每个节点内部的tmax了。

不过我们还需要想一下新加的两个变量：lmax（最大前缀和） 和 rmax（最大后缀和）如何得到。

和之前的思考方式类似，我们分情况来讨论：

对于一个父节点的lmax，我们也可以分为两种情况：

• ①没有跨过分界点，如下图，父节点lmax = 左儿子lmax。
  
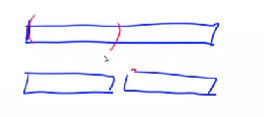
• ②跨过了分界点，如下图。
  

对于上方的情况②，我们发现运用现有的条件是无法得到的，父节点最大前缀和lmax 等于 左儿子区间总和 加上 右儿子lmax。

同理，父节点最大后缀和rmax 等于 右儿子区间总和 加上 左儿子rmax。

所以说，我们的节点最后还需要一个新的信息：区间和（设为sum）

而对于 父节点sum也是可以计算出来的，我们可以由左儿子sum 加上 右儿子sum，
表达式：父节点u.sum = L_son.sum + R_son.sum

我们综合一下得出两个关于最大前后缀和的表达式：

• ①父节点u.lmax = max{L_son.lmax, L_son.sum + R_son.lmax}

• ②父节点u.rmax = max{R_son.rmax, R_son.sum + L_son.rmax}

至此，我们已经能够确定好存储线段树的结构体包含了哪些变量，进而可以确定pushup函数的编写，整个编码的大体框架不变，由四个函数构成：pushup自子向父传递信息、build建立、modify修改、ask查询。

本题对于ask函数另有分类等细节处理，详见代码。

时间复杂度：

O(mlogn)（m<=1e5，n<=5e5）

代码：

#include<bits/stdc++.h>

using namespace std;

const int N = 5e5+10;
int a[N];
int n, m;
struct node
{
        int l, r;
        int tmax;
        int sum;
        int lmax, rmax;
} t[N<<2];

void pushup(node &u, node &l, node &r)
{
        u.sum = l.sum + r.sum;
        u.tmax = max(max(l.tmax, r.tmax), l.rmax+r.lmax);
        u.lmax = max(l.lmax, l.sum+r.lmax);
        u.rmax = max(r.rmax, r.sum+l.rmax);
}

void pushup(int u){
        pushup(t[u], t[u<<1], t[u<<1|1]);
}

void build(int u, int l, int r)
{
        t[u].l = l, t[u].r = r;
        if(l==r) { t[u].tmax = t[u].sum = t[u].lmax = t[u].rmax = a[l]; return ; }

        int mid = l+r>>1;
        build(u<<1, l, mid), build(u<<1|1, mid+1, r);
        pushup(u);
}

void modify(int u, int x, int v)
{
        if(t[u].l==t[u].r) { t[u] = {x, x, v, v, v, v}; return ;}
        int mid = t[u].l+t[u].r>>1;
        if(x<=mid) modify(u<<1, x, v);
        else modify(u<<1|1, x, v);
        pushup(u);
}

node ask(int u, int l, int r)
{
        if(l<=t[u].l&&r>=t[u].r) return t[u];

        int mid = t[u].l+t[u].r>>1;
        if(r<=mid) return ask(u<<1, l, r);
        else if(l>=mid+1) return ask(u<<1|1, l, r);
        else
        {
                auto left = ask(u<<1, l, r);
                auto right = ask(u<<1|1, l, r);
                node res;
                pushup(res, left, right);
                return res;
        }
}

int main()
{
        scanf("%d%d", &n, &m);
        for(int i=1;i<=n;++i) scanf("%d", &a[i]);

        build(1, 1, n);
        while(m--)
        {
                int k, x, y;
                scanf("%d%d%d", &k, &x, &y);

                if(k==1)
                {
                        if(x>y) swap(x, y);
                        printf("%d\n", ask(1, x, y).tmax);
                }
                else
                {
                        modify(1, x, y);
                }
        }


        return 0;
}