树状数组介绍（蓝书详细讲解）+ AcWing 241. 楼兰图腾（树状数组模板题 区间查询 单点修改 逆序对思想 ）

树状数组介绍以及如何用于求逆序对（蓝书讲解）：

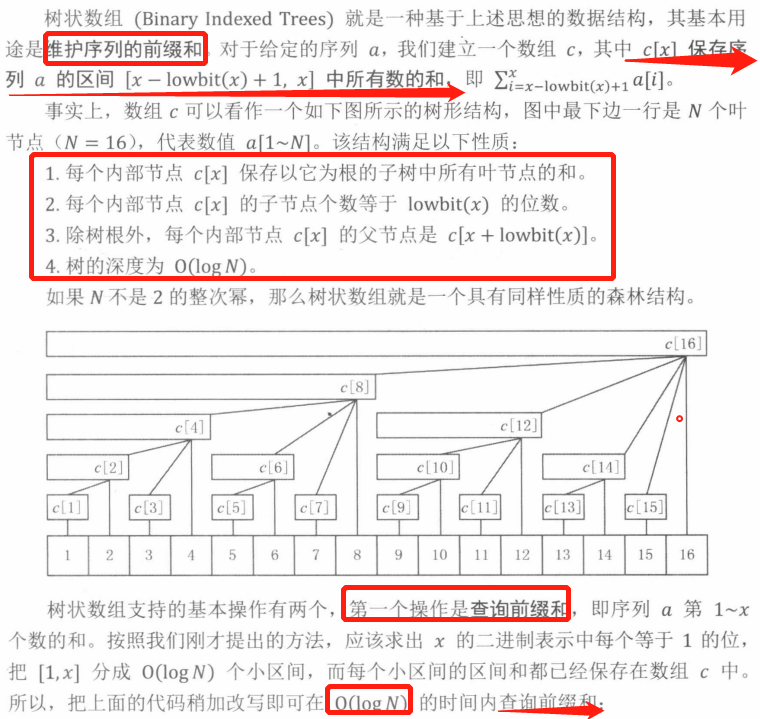
经典例题：AcWing 241. 楼兰图腾

本题只要求实现树状数组基本操作 区间查询 和 单点修改。

空白代码：

#include<bits/stdc++.h>

using namespace std;
#define int long long
const int N = 2e5+10;
int a[N], c[N], up[N], down[N];

inline int lowbit(int x) {return x & (-x);}

int ask(int x)
{
    int ans = 0;
    while(x) {ans+=c[x], x-=lowbit(x);}
    return ans;
}

void add(int x, int y)
{
    for(; x<=n; x+=lowbit(x)) c[x]+=y;
}

signed main()
{
    cin>>n;
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&a[i]);
        add(a[i], 1), up[i] = ask(n)-ask(a[i]), down[i] = ask(a[i]-1);
    }
    
    memset(c, 0, sizeof c);
    int res1 = 0, res2 = 0;
    for(int i=n; i>=1; --i)
    {
        add(a[i], 1);
        res1+=up[i]*(ask(n)-ask(a[i]));
        res2+=down[i]*ask(a[i]-1);
    }
    cout<<res1<<' '<<res2<<"\n";
    
    return 0;
}

讲解

题意：

平面上有N个点（N<=2e5，这就提示我们只能用O(n)或者O(nlogn)的算法了），每个点横、纵坐标范围都是1~N，任意两个点横、纵坐标不同。

若三个点(x1, y1)，(x2, y2)，(x3, y3)满足x1 < x2 < x3，y1 > y2且y3 > y2，则这三个点构成“v”形图腾。

若三个点(x1, y1)，(x2, y2)，(x3, y3)满足x1 < x2 < x3，y1 < y2且y3 < y2，则这三个点构成“^”形图腾。

题目让我们求给定平面上两种图腾的个数。

思路：

如果把这N个点按照横坐标排序，那么它们的纵坐标则是1~N的一个排列，我们将这个排列存入a数组。

在刚刚讲述的树状数组求逆序对中，我们知道了如何在一个序列中计算每个数的后面有多少个数比它小，类似这个做法，我们可以：

• ①正序扫描序列，利用树状数组将每一个a[i]前面有几个数比它大（ask(n)-ask(a[i])）,有几个数比它小（ask(a[i]-1)）求出。并将这些值先分别存入up[i]和down[i]，方便后续运算。

• ②倒序扫描序列，利用树状数组将每一个a[i]后面有几个数比它大（ask(n)-ask(a[i])）,有几个数比它小（ask(a[i]-1)）求出。

在倒序的过程中，我们可以依次次枚举每个点作为中间点，以这个点为中心的“v”图腾个数根据乘法原理显然是up[i]*(ask(n)-ask(a[i]))，所以总的“v”图腾个数就是将n个点算出来的值累加即可。同理，在此过程中也可求出“^”图腾的总个数。

（up[i]是正序扫描时求得的当前点前面比它大的元素个数，ask(n)-ask(a[i])是倒序扫描时当前点后面比它大的元素个数，相乘即为答案）

重点代码片段：

树状数组c初始化 ：O(nlogn)

比如我们想对包含n个元素的序列a建立一个树状数组，
建立一个全0的数组c，对每个位置x执行add(x, a[x])。

memset(c, 0, sizeof c);
for(int i=1;i<=n;++i) add(i, a[i]);

倒序查询1~x前缀和 ：O(logn)

int ask(int x)
{
    int ans = 0;
    while(x) {ans+=c[x], x-=lowbit(x);}
    return ans;
}

正序单点修改 ：O(logn)

void add(int x, int y)
{
    for(; x<=n; x+=lowbit(x)) c[x]+=y;
}

时间复杂度：

nlogn

代码：

#include<bits/stdc++.h>

using namespace std;
#define int long long
const int N = 2e5+10;
int a[N], c[N], up[N], down[N];
//a存储n个点的纵坐标，c表示树状数组i结点覆盖的范围和，up表示左边比第i个位置大的数的个数，down表示左边比第i个位置小的数的个数
int n;

inline int lowbit(int x) {return x & (-x);}

int ask(int x)//查询序列1~x前缀和
{
    int ans = 0;
    while(x) {ans+=c[x], x-=lowbit(x);}
    return ans;
}

void add(int x, int y)//将第x个数加上y，构建树状数组c
{
    for(; x<=n; x+=lowbit(x)) c[x]+=y;
}

signed main()
{
    cin>>n;
    for(int i=1;i<=n;++i)//正序依次统计每个位置左边比第i个数纵坐标y小的数的个数、以及大的数的个数
    {
        scanf("%d",&a[i]);
        add(a[i], 1), up[i] = ask(n)-ask(a[i]), down[i] = ask(a[i]-1);
//add(a[i], 1);---将y加入树状数组，即数字y出现1次
//up[i] = ask(n)-ask(a[i]);---在前面已加入树状数组的所有数中统计在区间[y + 1, n]的数字的出现次数
//down[i] = ask(a[i]-1);---在前面已加入树状数组的所有数中统计在区间[1, y - 1]的数字的出现次数
    }
    
    memset(c, 0, sizeof c);//清空树状数组，
    int res1 = 0, res2 = 0;
    for(int i=n; i>=1; --i)//倒序统计每个位置右边比第i个数y小的数的个数、以及大的数的个数
    {
        add(a[i], 1);
        res1+=up[i]*(ask(n)-ask(a[i]));//乘法原理
        res2+=down[i]*ask(a[i]-1);
    }
    cout<<res1<<' '<<res2<<"\n";
    
    return 0;
}