【机器学习】机器学习的基本分类-无监督学习-DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

DBSCAN 是一种基于密度的聚类算法，能够发现任意形状的簇，并有效识别噪声点。它通过数据点的密度分布来定义簇，避免了指定簇数量 k 的需求。

---

1. 算法简介

基本概念

1. 核心点 (Core Point)：
   • 在半径 内包含至少 个点的点。
2. 边界点 (Border Point)：
   • 在 半径内点数不足 ，但位于核心点的 -邻域内的点。
3. 噪声点 (Noise Point)：
   • 既不是核心点也不是边界点的点。

参数

1. (Epsilon)：定义一个点的邻域半径。
2. ：一个点被定义为核心点所需的最少点数（包括点自身）。

聚类过程

1. 如果一个点是核心点，聚类算法将其 -邻域内的所有点归为同一个簇。
2. 重复直到没有新的点可以加入。
3. 未分配到任何簇的点被标记为噪声。

---

2. 算法步骤

1. 初始化：
   • 设置 和 参数。
   • 标记所有点为未访问。
2. 从未访问点开始遍历：
   • 如果某点未访问，计算其 -邻域点。
   • 如果邻域点数量 ，将该点标记为核心点，形成新簇。
   • 否则，将其标记为噪声点。
3. 扩展簇：
   • 对新簇中所有核心点的邻域点进行扩展，合并到当前簇。
4. 终止条件：
   • 直到所有点都被访问。

---

3. 特点

优点

1. 无需预设簇数量 k：适用于对簇数未知的问题。
2. 可识别任意形状簇：适用于非凸形状的聚类。
3. 鲁棒性强：对噪声点和异常值不敏感。

缺点

1. 参数敏感： 和 参数需要调试，选择不当会显著影响结果。
2. 高维数据表现不佳：密度的定义在高维空间中变得不明显。
3. 计算复杂度高：尤其是大数据集，计算 -邻域的代价较高

---

4. 参数选择方法

1. 的选择：
   • 使用 k-距离图 (k-distance plot)：对数据点计算最近 -邻居距离，选择“肘部”点作为 。
2. 的选择：
   • 通常设定为数据集维度的两倍。例如，对于二维数据， 是常见选择。

---

5. DBSCAN 的实现

Python 实现（使用 scikit-learn）

from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt

# 生成数据
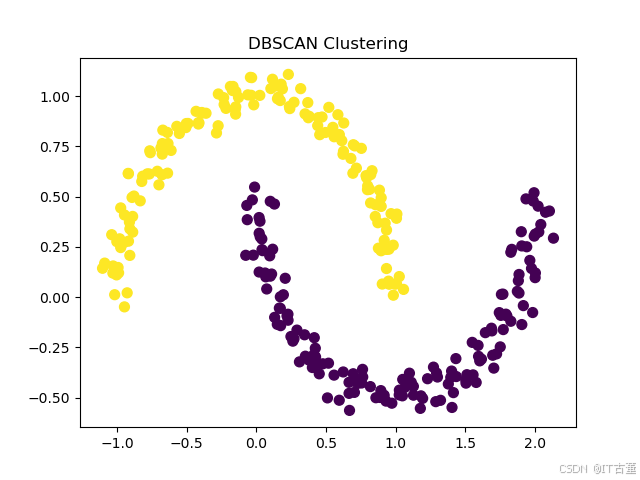
X, _ = make_moons(n_samples=300, noise=0.05, random_state=42)

# DBSCAN 聚类
dbscan = DBSCAN(eps=0.2, min_samples=5)
clusters = dbscan.fit_predict(X)

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap='viridis', s=50)
plt.title('DBSCAN Clustering')
plt.show()

---

6. 应用场景

1. 地理空间分析：
   • 识别地震震中、热点区域等。
2. 图像处理：
   • 分割图像中的像素点簇。
3. 市场分析：
   • 识别异常交易行为。
4. 文本分析：
   • 文本嵌入后的聚类。

---

7. 评价指标

轮廓系数 (Silhouette Coefficient)：

衡量聚类的紧密性和分离性：

• a：样本点到同簇内其他点的平均距离。
• b：样本点到最近簇内点的平均距离。

噪声点的影响：

观察算法将多少数据点标记为噪声，评估 和 的合理性。

---

8. DBSCAN 与其他算法对比

特性	DBSCAN	K-Means	层次聚类
簇数量	自动确定	需预设	可自动生成
簇形状	任意形状	仅适用凸簇	任意形状
噪声处理	能识别噪声	对噪声敏感	对噪声敏感
扩展性	中等	高	较差

---

 DBSCAN 是一种功能强大的聚类算法，适用于各种实际场景。然而，它对参数敏感，适用于中小型数据集。在高维和大数据场景下，需结合降维和加速策略以提高性能。