python 聚类分析实战案例:K-means算法(原理源码)

K-means算法：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xvV44zrK-1573127992123)(https://img-blog.youkuaiyun.com/20171220143951780?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvSEhUTkFO/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)]
关于步骤：参考之前的博客
关于代码与数据：暂时整理代码如下：后期会附上github地址，上传原始数据与代码完整版，

各种聚类算法的对比：参考连接
Kmeans算法的缺陷

1.聚类中心的个数K 需要事先给定，但在实际中这个 K 值的选定是非常难以估计的，很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适
2.Kmeans需要人为地确定初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果。

#!usr/bin/env python
#_*_ coding:utf-8 _*_
import random
import math
'''
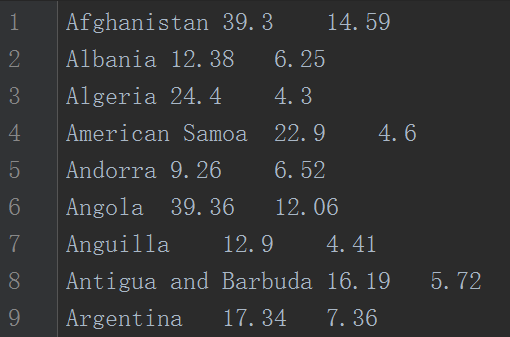
kMeans:2列数据对比，带有head
'''
#1.load data
def importData():
   f = lambda name,b,d: [name, float(b), float(d)]

   with open('birth-death-rates.csv', 'r') as inputFile:
          return [f(*line.strip().split('\t')) for line in inputFile]

写入文件类型

**#2. calculate Distance **

def euclideanDistance(x,y):
    return math.sqrt(sum([(a-b)**2 for (a,b) in zip(x,y)]))

#L=points,
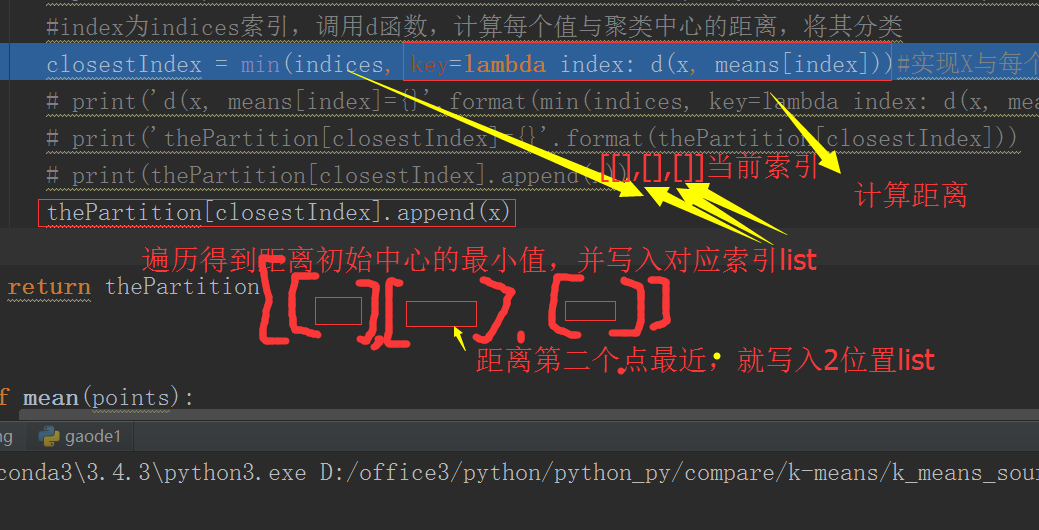
def partition(points, k, means, d=euclideanDistance):
   # print('means={}'.format(means))
   thePartition = [[] for _ in means]  # list of k empty lists

   indices = range(k)
   # print('indices={}'.format(indices))

   for x in points:
    
      #index为indices索引，调用d函数，计算每个值与聚类中心的距离，将其分类
      closestIndex = min(indices, key=lambda index: d(x, means[index]))#实现X与每个Y直接的求解：key=lambda index: d(x, means[index])
    
      thePartition[closestIndex].append(x)

   return thePartition

#3.寻找收敛点
def mean(points):
   ''' assume the entries of the list of points are tuples;
       e.g. (3,4) or (6,3,1). '''

   n = len(points)
   # print(tuple(float(sum(x)) / n for x in zip(*points)))   #*points将【[1，2]，[2，3]】分割出来【1，2】
   return tuple(float(sum(x)) / n for x in zip(*points))  #将最开始的[[4, 1], [1, 5]] 经过处理变成[（4, 1）,（1, 5）]


def kMeans(points, k, initialMeans, d=euclideanDistance):
   oldPartition = []
   newPartition = partition(points, k, initialMeans, d)

   while oldPartition != newPartition:
      oldPartition = newPartition
      newMeans = [mean(S) for S in oldPartition]
      newPartition = partition(points, k, newMeans, d)

   return newPartition

#0.函数调用初始中心点

if __name__ == "__main__":
   L = [x[1:] for x in importData()] # remove names
   # print (str(L).replace('[','{').replace(']', '}'))
   import matplotlib.pyplot as plt
   '''
   plt.scatter(*zip(*L))
   plt.show()
   '''
   import random
   k = 3
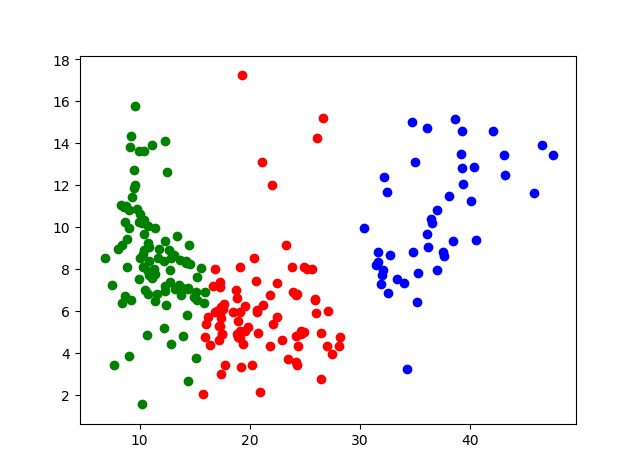
   partition = kMeans(L, k, random.sample(L, k))  #L是集合，K分类个数，random.sample(L, k)中心点
   plt.scatter(*zip(*partition[0]), c='b')#[[],[],[]]
   plt.scatter(*zip(*partition[1]), c='r')
   plt.scatter(*zip(*partition[2]), c='g')
   plt.show()