Day 59 经典时序模型3

@浙大疏锦行

今日任务：

1. SARIMA模型的参数和用法：SARIMAR(p,d,q)(P,D,Q)m
2. 模型结果的检验可视化：对摘要表的可视化
3. 多变量数据：内生变量和外部变量
4. 多变量模型：统计模型；机器学习模型；深度学习模型

作业：尝试实战SARIMAX模型

一、SARIMA模型

从AR、MA，到混合的ARMA，到加入普通差分的ARIMA，再到加入季节性差分的SARIMA模型，它们一步步从基础复合到SARIMA(p,d,q)(P,D,Q)m。

1.1 参数

SARIMA模型由两组参数组成：

• 非季节性部分：(p,d,q)，这个与ARIMA相同 —— 站在普通视角（前后时刻）
• 季节性部分：(P,D,Q,m)，负责处理序列的长期、周期性依赖关系——站在季节视角（不同季节的同一时刻）

（1）m：数据本身固有的、预先定义的结构属性，可以理解为季节周期。比如月度数据，m=12；季度数据，m=4。

（2）(p,d,q)和(P,D,Q)：本质做的事情一样，区别在于时间点的不同（前后时刻与前后周期）

• p和P：自回归。普通AR (p) 认为 y_t 和 y_{t-1}, y_{t-2}等相关。季节性AR (P) 认为 y_t 和 y_{t-m}, y_{t-2m}等相关
• d和D：差分。普通差分 (d) 是 y_t - y_{t-1} (今天 - 昨天)。季节性差分 (D) 是 y_t - y_{t-m} (今年8月 - 去年8月)。
• q和Q：移动平均。普通MA (q) 认为 y_t 的误差和 t-1, t-2 时刻的误差相关。季节性MA (Q) 认为 y_t 的误差和 t-m, t-2m 时刻的误差相关

1.2 完整工作流

总体上，与之前不嵌入模型，单独处理的顺序相似：先进行季节性处理（季节性部分），然后再普通差分去除趋势（非季节性部分）：

（1）季节性层面：模型首先利用 (P, D, Q)m 这一套完整的“季节性ARIMA”来处理数据。它从季节性差分(D) → 季节性自回归(P)和季节性移动平均(Q) → 解释季节性平稳后的数据中的模式。这个过程的输出是一个“季节性影响被剥离后”的残差序列。

（2）非季节性层面：接着，模型再将我们熟悉的 (p, d, q) 应用于第一步产生的残差序列上。普通差分(d) → AR(p)和MA(q) → 捕捉其中剩余的、短期的、非季节性的模式。

总结：SARIMA不是在ARIMA上打个补丁，而是构建了一个与非季节性部分 (p,d,q) 平行且完整的季节性分析系统 (P,D,Q)m。这两个系统协同工作，一个负责宏观的、周期性的规律，另一个负责微观的、短期的波动，最终结合成一个强大而全面的预测模型。

二、实战

2.1 可视化原始数据

读取本地数据集，观察原始数据的特征（趋势和季节性）

注：将month列转换为日期格式

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.statespace.sarimax import SARIMAX
import warnings
warnings.filterwarnings('ignore')
# 显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# 1. 加载数据
df = pd.read_csv('AirPassengers.csv',index_col=0) # 第一列month作为索引
df.rename(columns={'#Passengers': 'Passengers'}, inplace=True)
df.index = pd.to_datetime(df.index) # 将month转换为日期格式
df.head()

# 划分测试集和训练集
train_data = df.iloc[:-12]
test_data = df.iloc[-12:] # 使用最后一年的数据作为测试集

# 可视化原始数据
plt.figure(figsize=(12,6))
plt.plot(train_data['Passengers'],label='Train')
plt.plot(test_data['Passengers'],label='Test',color='coral')
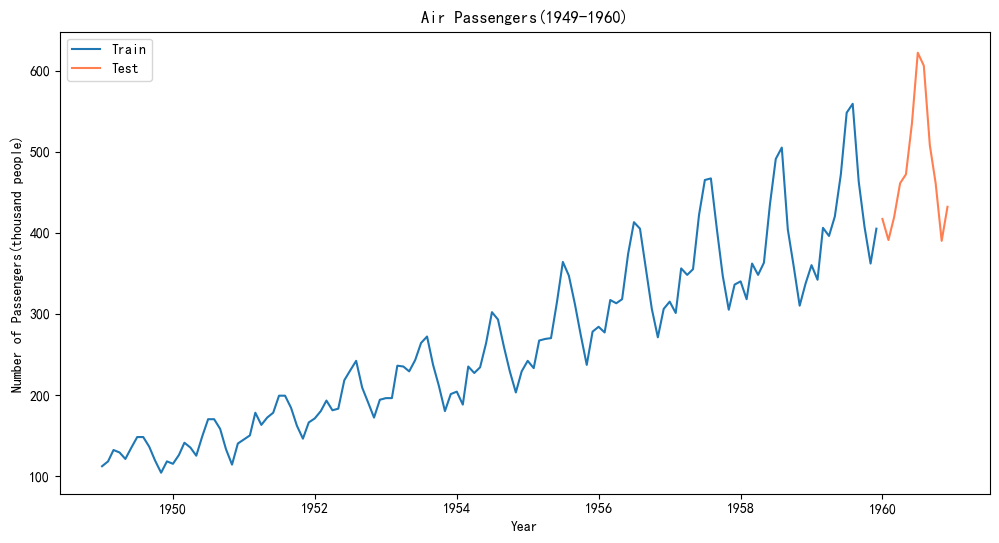
plt.title('Air Passengers(1949-1960)')
plt.xlabel('Year')
plt.ylabel('Number of Passengers(thousand people)')
plt.legend()
plt.show()

# 平稳性检验
result = adfuller(df)
print(f'p-value:{result[1]}')

存在明显的上升趋势以及季节性变化

2.2 差分阶数

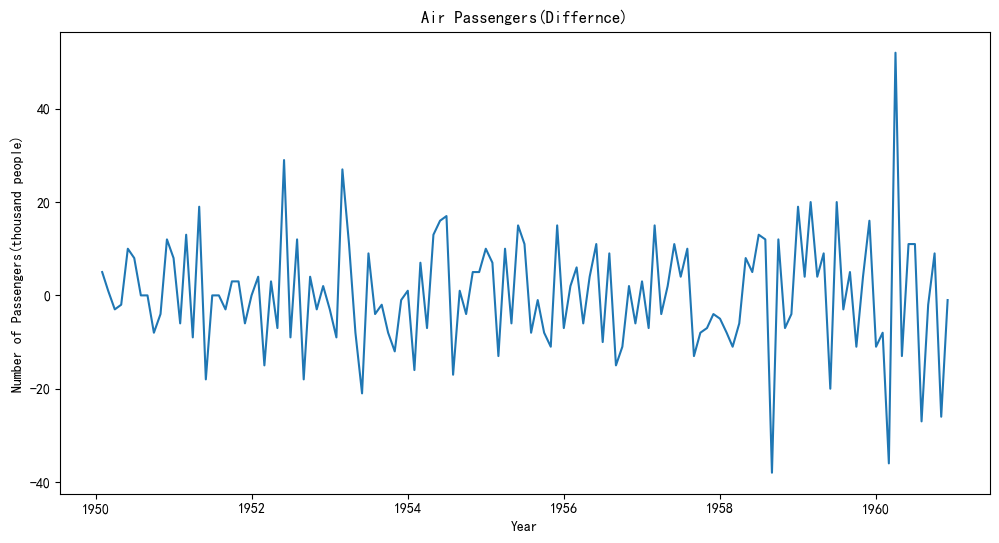
数据存在季节性 → m=12。对于差分阶数，先尝试D=1,d=1，查看ADF检验的结果，判断是否进一步差分。

# 差分阶数
seasonal_df = df.diff(periods=12).dropna() # 季节性差分，D=1
seasonal_df_diff = seasonal_df.diff().dropna() # 普通差分,d=1

# 可视化
plt.figure(figsize=(12,6))
# plt.plot(df['Passengers'],label='Origin')
plt.plot(seasonal_df_diff['Passengers'])
plt.title('Air Passengers(Differnce)')
plt.xlabel('Year')
plt.ylabel('Number of Passengers(thousand people)')
plt.show()

result_diff = adfuller(seasonal_df_diff)
print(f"p-value:{result_diff[1]}")

原始：p-value:0.991880243437641
季节性差分：p-value:0.011551493085514954
季节性+普通差分：p-value:1.856511600123444e-28

2.3 超参数搜索确定p,q

可以使用ACF和PACF图，然后通过截尾和拖尾的特征来判断，但是可能不够准确且麻烦。

# 绘制ACF和PACF图
fig,(ax1,ax2) = plt.subplots(2,1,figsize=(12,6))
plot_acf(seasonal_df_diff,lags=40,ax=ax1)
plot_pacf(seasonal_df_diff,lags=40,ax=ax2)
plt.tight_layout()
plt.show()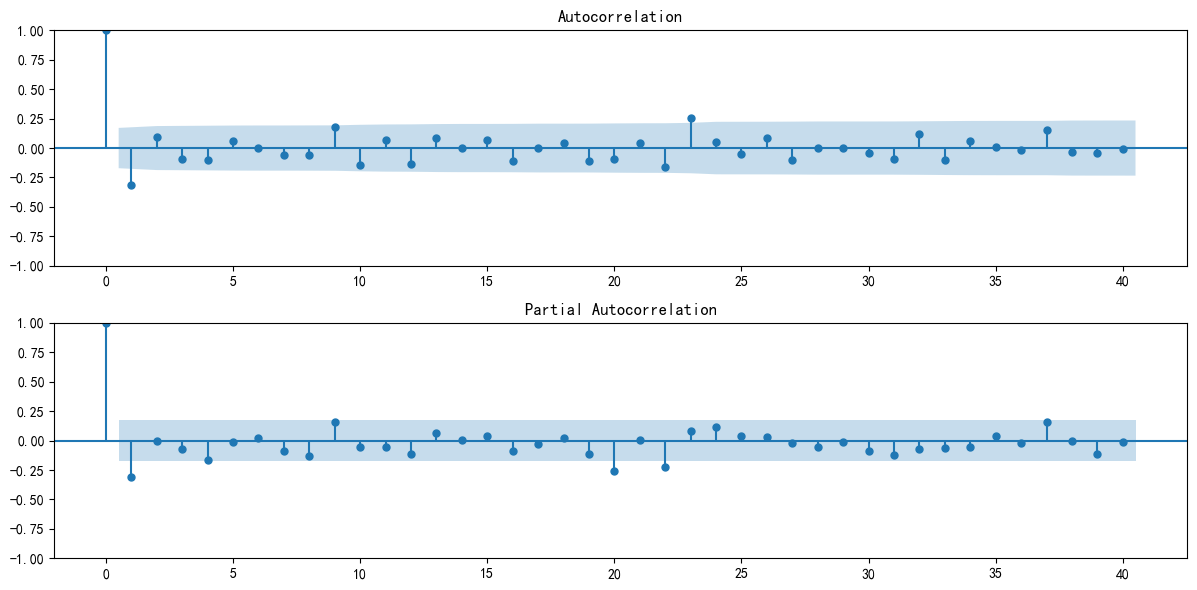

这里使用pmdarima库中auto_arima进行自动调参（默认使用AIC作为评估标准，AIC越小越好），确定(p,q)和(P,Q)。

# 超参数搜索
from pmdarima import auto_arima # 一个方便的自动调参库
# 使用auto_arima自动寻找最优模型
# 我们告诉它d=1, D=1, m=12是固定的，让它去寻找p,q,P,Q的最优组合
# 默认使用AIC作为评估标准
auto_model = auto_arima(train_data['Passengers'],
                        start_p=0, start_q=0,
                        max_p=2, max_q=2,
                        m=12,
                        start_P=0, seasonal=True,
                        d=1, D=1,
                        trace=True,
                        error_action='ignore',
                        suppress_warnings=True,
                        stepwise=True)

print(auto_model.summary())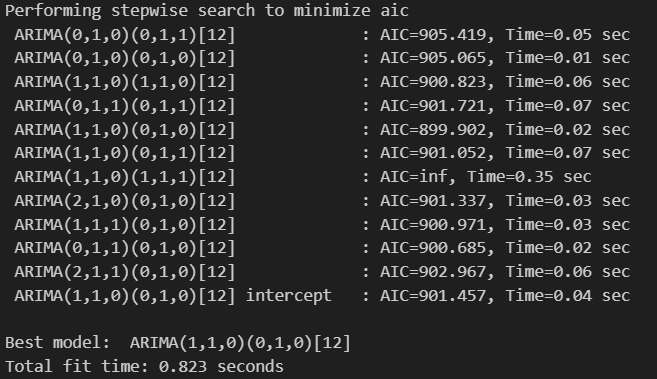

2.4 模型诊断可视化

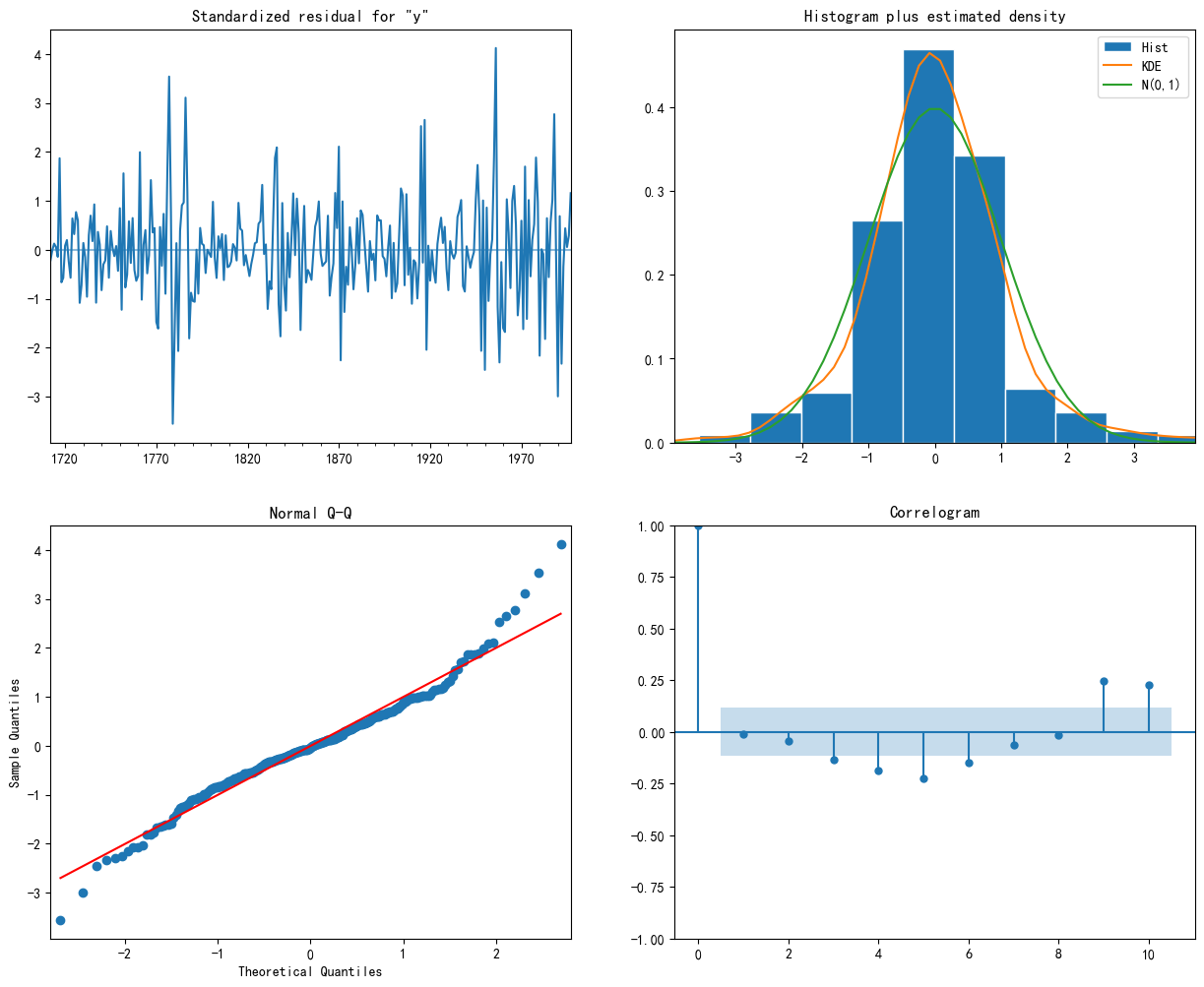
获取最优参数，拟合模型。然后绘制模型诊断图，检验残差是否满足白噪声的假设：

• 标准化残差图：残差值随时间的变化，理想情况是随机波动，无异方差性（方差稳定）。
• 直方图+核密度估计：是否符合正态分布。
• 正态Q-Q图：检验正态分布。理想情况是散点紧密排列在对角线上
• 相关图（ACF图）：检验独立性。理论上，所有自相关系数（柱子）都应在蓝色置信区间内

# 从auto_arima的结果中获取最优参数

best_order = auto_model.order
best_seasonal_order = auto_model.seasonal_order

# 拟合模型
model = SARIMAX(train_data['Passengers'],
                order=best_order,
                seasonal_order=best_seasonal_order)
results = model.fit(disp=False)

# 打印模型诊断图
results.plot_diagnostics(figsize=(15, 12))
plt.show()

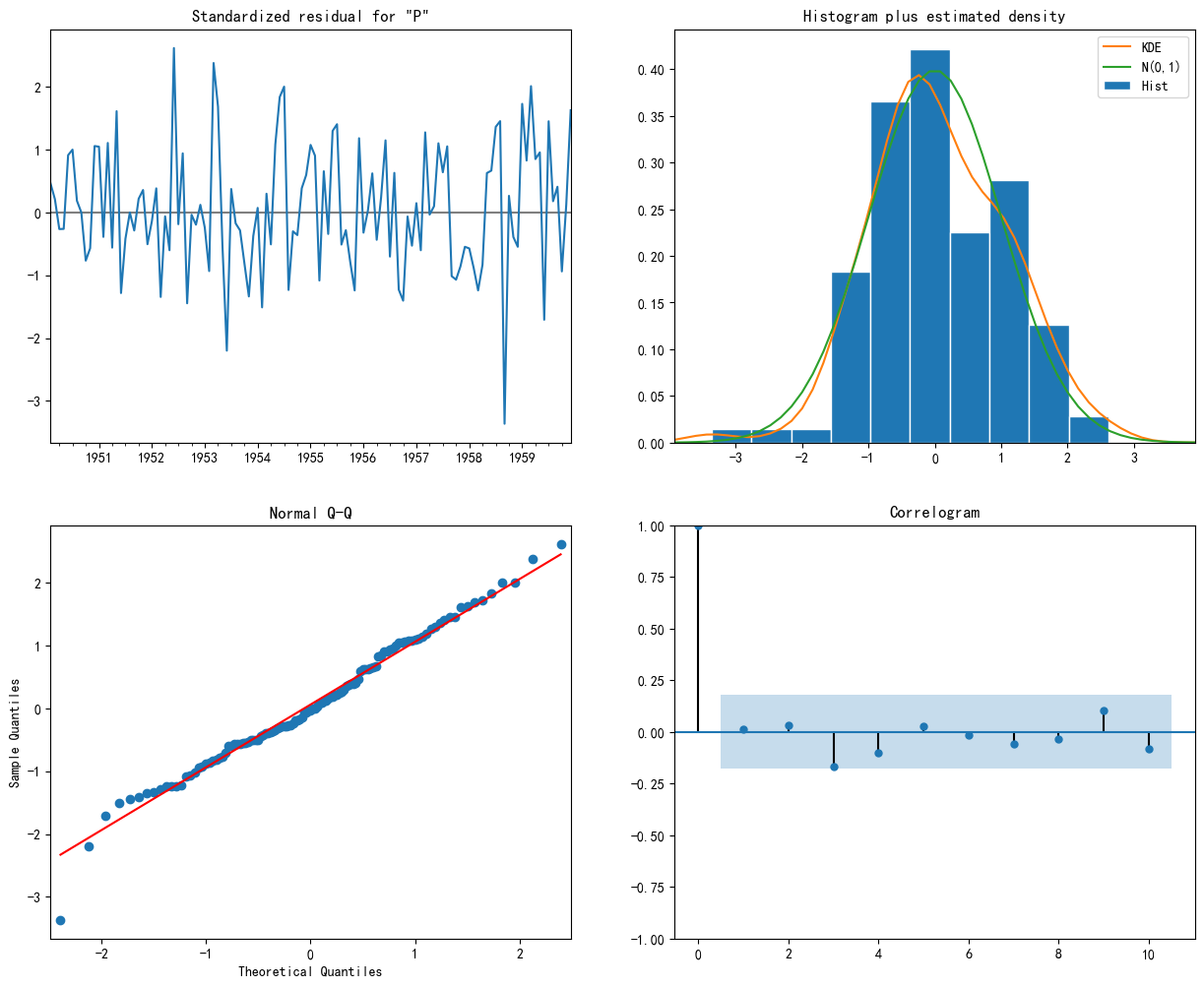
若不理想：

• ACF图有显著相关 → 可能需要增加 MA 或 seasonal MA 项
• 残差非正态 → 考虑对数据做变换（如对数变换）
• 残差有趋势 → 可能需要增加差分阶数

2.5 预测结果

预测未来12个点（一个周期）。

get_prediction:获取样本内外的预测（可指定起止点）；只预测样本外时，相当于get_forecast(只能指定步数)。

注：捕捉到波峰和波谷 → 准确预测季节性

# 预测结果
# get_prediction:获取样本内外的预测（可指定起止点）；只预测样本外时，相当于get_forecast(只能指定步数)
forecast = results.get_prediction(start=test_data.index[0],end=test_data.index[-1])
pred_mean = forecast.predicted_mean
conf_int = forecast.conf_int()

plt.figure(figsize=(12,6))
plt.plot(df['Passengers'],label='Origin')
plt.plot(pred_mean,label='SARIMA Predicted')
plt.fill_between(conf_int.index,
                 conf_int.iloc[:, 0],
                 conf_int.iloc[:, 1], color='pink', alpha=0.5, label='Confidence Interval')
plt.title('Air Passengers: Origin vs Predicted')
plt.xlabel('Year')
plt.ylabel('Number of Passengers(thousand people)')
plt.show()

二、多变量时序任务

2.1 多变量数据

单变量数据的y是标量（单个值），而多变量的y是向量（多个值）

• 单变量数据：每个时间点，只记录一个值。[时间1，乘客数1]，[时间2，乘客数2]...
• 多变量数据：每个时间段，同时记录多个变量（通常变量间相互关联、影响）的值。如时间x → [体温，心率，血压，呼吸频率]y

在多个变量中，想要预测的变量叫目标变量（内生变量--标签），其它的叫外部变量（外生变量--特征）。

2.2 常见的多变量预测模型

主要有三类：

• 经典统计模型：基于严格的统计假设，模型结构清晰，解释性强
• 机器学习模型：将时序问题转换为监督问题，灵活性高，能处理复杂关系
• 深度学习模型：专门为序列数据涉及，能自动学习复杂的时序模式和长期依赖

2.2.1 Classical Statistical Models

2.2.1.1 SARIMAX

SARIMAX（Seasonal ARIMA with eXogenous variables），在SARIMA的基础上加入了X（eXogenous，外生变量）。

• 非季节性核心 (ARIMA部分): (p, d, q)，负责捕捉数据的长期趋势和非季节性自相关性。
• 季节性核心 (Seasonal部分): (P, D, Q, m)，负责处理数据的周期性模式。
• 外部影响核心 (eXogenous部分): X，负责量化一个或多个外部变量对目标变量的影响。

模型首先像SARIMA一样，分析目标序列 y 自身的历史模式（趋势、季节性等）。然后，它同时建立一个类似线性回归的模型，来评估外生变量 X 是如何影响 y 的。最终的预测结果是这两部分作用的结合。

y_t = f(过去的y值, 过去的误差)（ARIMA模型） + β * x_t（线性回归）

其中 ，y_t 是想预测的目标变量在时间 t 的值，x_t 是外生变量在时间 t 的值，而 β 是一个系数，表示 x_t 对 y_t 的影响程度。如果 β 为正，说明 x 和 y 是正相关；如果为负，则为负相关。

SARIMAX适用于：（1）因果清晰且单向：数据含义简单，不存在循环依赖（2）未来的X是已知或可预测：未来的x和过去的x关系必须简单，如特征是周几，今天是周一，那么明天必定是周二

• 优点：解释性强，每个外生变量的系数β意义明确，加入季节性处理
• 缺点：严格的单向因果假设。y不能反过来影响x，必须提供未来的x值来预测未来。

2.2.1.2 VAR

现实中，存在许多因果的循环依赖：

如果忽略变量间的循环依赖关系，只考虑单边的内生与外生关系，显然是不合理的。因此，VAR模型应运而生。

VAR模型：系统中的每个变量，都可以用系统内所有变量的过去值来预测。在系统中的每个变量都是内生变量，不再区分内生与外生。

2.2.1.3 小结

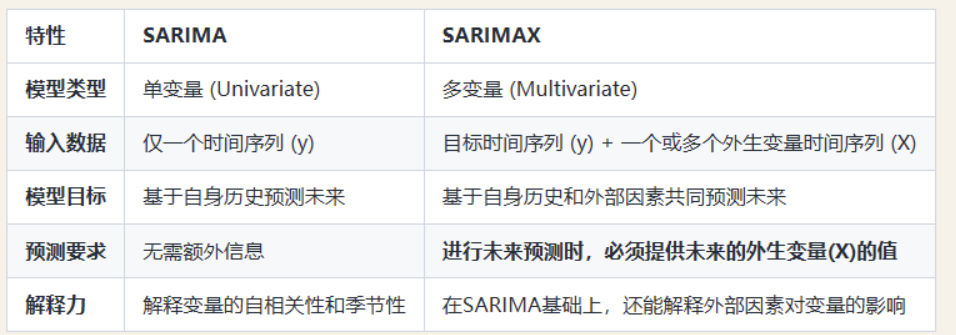
2.2.2 Machine Learning Models

核心：通过滑动窗口，将时序问题转换为监督问题。

常见处理思路：

• 线性部分：先使用统计模型SARIMA作为特征提取器，预测趋势、季节性；
• 非线性（残差）：再使用XGBoost或LightGBM进行预测。

2.2.3 Deep Learning Models

深度学习：“万能函数拟合器”，学习不平稳模式本身，避免繁琐的假设验证。

（1）先让“结构工程师”（分解模型）把宏观的、确定的趋势和季节性部分拿走。（2）然后，把剩下的、更接近平稳的、但仍然包含一些微弱信息的“残差”，交给“精装修师傅”（ARIMA）去处理。（3）最后，将两部分的工作成果合起来，得到最终的精美成品（预测结果）。

特征提取与参数：

• ACF/PACF图选择sequence_length：一个值和它过去多少个值有关系。比如，如果ACF图显示季节性周期是12，那么你在设置LSTM的“回看窗口”(sequence_length)时，把它设为12或其倍数，可能会是一个非常好的起点。
• 平稳性检验做特征工程：如果你通过检验发现数据有强烈的趋势，即使LSTM能学，你也可以通过一些简单的处理来“帮助”它学得更好、更快。
• 差分：对数据做一次差分，然后让LSTM去预测这个“变化量”，最后再把结果加回去。这常常能让模型训练更稳定。
• 添加时间特征：把“月份”、“星期几”作为额外的特征输入给模型，等于明确地告诉模型：“注意，这里面有周期性规律！”，帮助它更快地捕捉到季节性。

三、太阳黑子数据SARIMAX模型实战

from statsmodels.datasets import sunspots
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX

# 设置matplotlib以正确显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

df_sun = sunspots.load_pandas().data['SUNACTIVITY']
years = pd.to_datetime(range(1700, 1700 + len(df_sun)),format='%Y')
df_sun = pd.Series(df_sun.values,index=years) # 1700-2008
df_sun.head()

train_data = df_sun[:-11] # 1700-1997
test_data = df_sun.iloc[-11:] # 1998-2008

# 平稳性检验
print('--- ADF检验结果 ---')
# H0: 序列非平稳; H1: 序列平稳
result = adfuller(df_sun)
p_value = result[1]
print(f'p-value:{p_value}')
if p_value <= 0.05:
    print('结论: 拒绝原假设，序列是平稳的。')
else:
    print('结论: 未能拒绝原假设，序列是非平稳的。')

# 差分处理：周期性，period=11
df_sun_period = df_sun.diff(periods=11).dropna()
result_period = adfuller(df_sun_period)
print(f"p-value:{result_period[1]}")
if result_period[1] <= 0.05:
    print('结论: 拒绝原假设，序列是平稳的。')
else:
    print('结论: 未能拒绝原假设，序列是非平稳的。')

# 绘制原始图像
plt.figure(figsize=(12,6))
plt.subplot(211)
plt.plot(df_sun)
plt.title("太阳黑子数量(原始)")
plt.xlabel('年')
plt.ylabel('观测数量')
    
plt.subplot(212)
plt.plot(df_sun_period)
plt.title("太阳黑子数量(差分后)")
plt.xlabel('年')
plt.ylabel('观测数量')
plt.tight_layout()
plt.show()

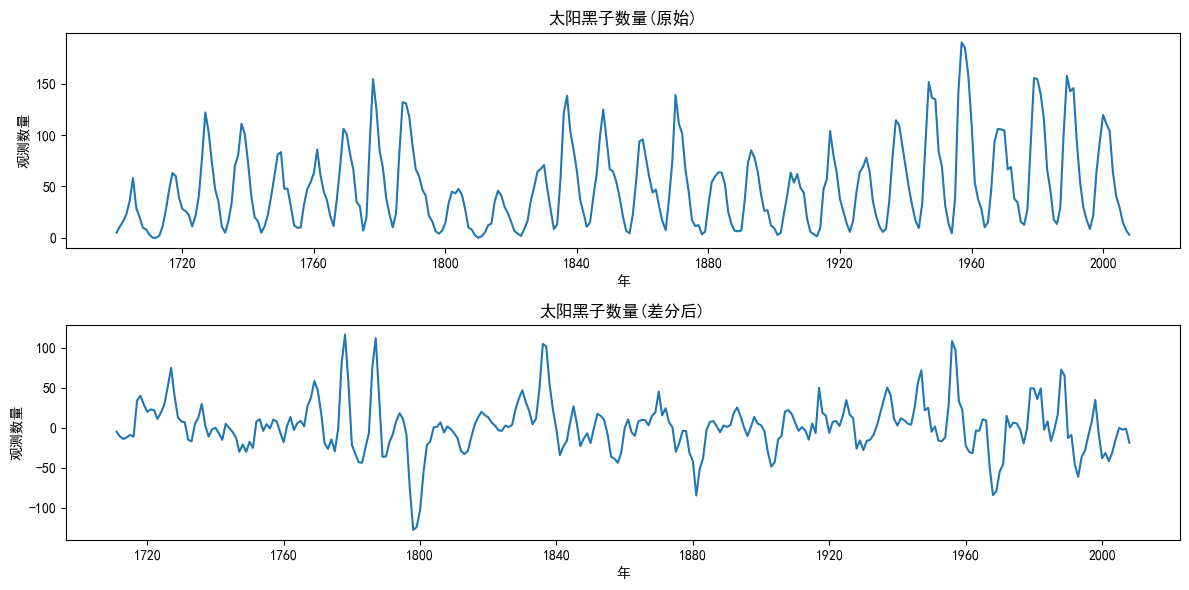
# 超参数搜索
from pmdarima import auto_arima # 一个方便的自动调参库
# 使用auto_arima自动寻找最优模型
# 我们告诉它d=1, D=1, m=12是固定的，让它去寻找p,q,P,Q的最优组合
# 默认使用AIC作为评估标准
auto_model = auto_arima(train_data,
                        start_p=0, start_q=0,
                        max_p=2, max_q=2,
                        m=11,
                        start_P=0, seasonal=True,
                        d=1, D=1,
                        trace=True,
                        error_action='ignore',
                        suppress_warnings=True,
                        stepwise=True)

print(auto_model.summary())

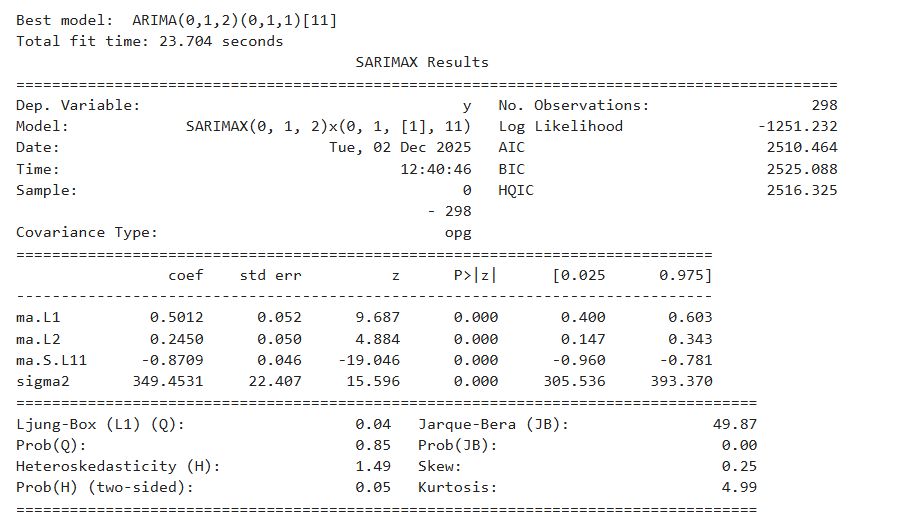
最佳模型参数为(0,1,2)(0,1,1)[11]

# 建模

# 获取最佳参数
best_order = auto_model.order # 非季节性参数
best_seasonal_order = auto_model.seasonal_order # 季节性参数

# 拟合模型
model = SARIMAX(train_data,order=best_order,seasonal_order=best_seasonal_order)
results = model.fit(disp=False) # display:是否显示拟合过程中的优化信息

# 模型诊断图
results.plot_diagnostics(figsize=(15,12))
plt.show()

存在自相关性、整体符合正态分布

# 预测未来12个点
predictions = results.get_prediction(start=test_data.index[0], end=test_data.index[-1])
pred_mean = predictions.predicted_mean # 预测均值
pred_ci = predictions.conf_int() # 预测的置信区间

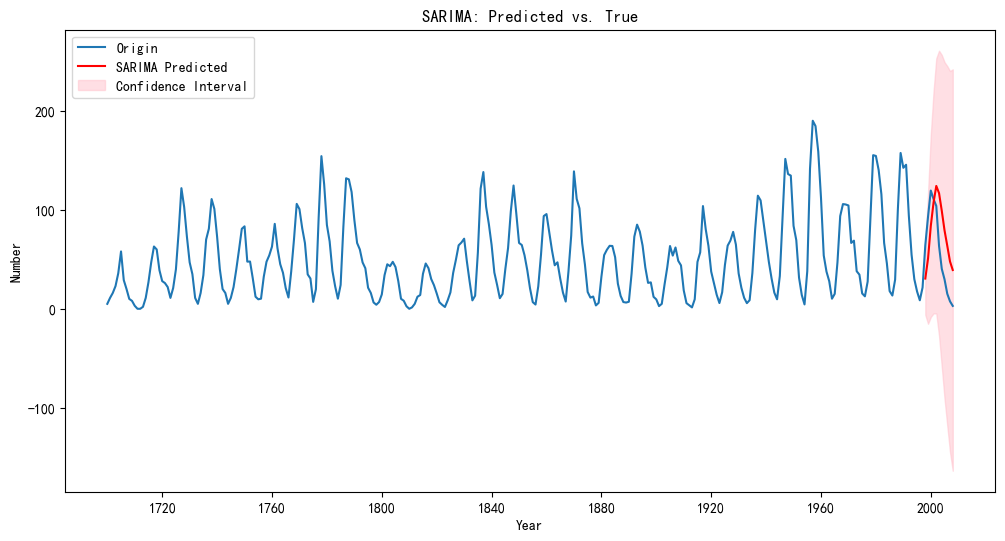
# 绘制预测结果
plt.figure(figsize=(12, 6))
plt.plot(df_sun, label='Origin')
plt.plot(pred_mean, label='SARIMA Predicted', color='red')
plt.fill_between(pred_ci.index,
                 pred_ci.iloc[:, 0],
                 pred_ci.iloc[:, 1], color='pink', alpha=0.5, label='Confidence Interval')
plt.title('SARIMA: Predicted vs. True')
plt.xlabel('Year')
plt.ylabel('Number')
plt.legend()
plt.show()