今日任务:
- 序列数据的处理:非平稳性(n阶差分);季节性(季节性差分);自回归性
- 模型选择:AR自回归模型;MA移动平均模型;ARMA自回归滑动平均模型
作业:检索经典的时序单变量数据集有哪些,选择一个尝试观察其性质
一、序列数据的处理
由于绝大多数经典的时间序列模型都建立在一个基本假设:数据的统计特性是恒定的(即平稳性),因此在数据处理时要保证这一点。
如果一个数据是平稳的,那么在图像上,它应该会表现出在某个位置附近来回波动,但整体不存在明显的趋势(上升或下降)。
针对趋势性问题,常用的方法是差分。差分的核心思想:用当前值减去前一个(或前几个)时间点的值,从而关注数据的变化速度、去除趋势。
下面使用一阶差分法,处理非平稳性和季节性。
1.1 非平稳性
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# 设置中文字体,防止matplotlib显示乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 1. 生成一段非平稳数据(随机游走+趋势)
np.random.seed(42)
# 随机游走部分
random_walk = np.random.randn(500).cumsum() # 累积和生成随机游走
# 添加一个线性趋势
trend = np.linspace(0, 100, 500)
# 合成我们的时序数据
data = pd.Series(random_walk + trend)
data.index = pd.date_range(start='2022-01-01', periods=500) # 时间索引首先生成非平稳性的数据,这里有一个数学模型——随机游走模型:
- 用来描述随机过程中的路径变化,每一步的方向和大小是随机确定的,且相互独立
- 可用来模拟股票价格、分子运动、赌博结果等不确定现象
然后对比使用差分处理前后的ADF结果变化:
# 2. 诊断原始数据
plt.figure(figsize=(12, 6))
plt.plot(data)
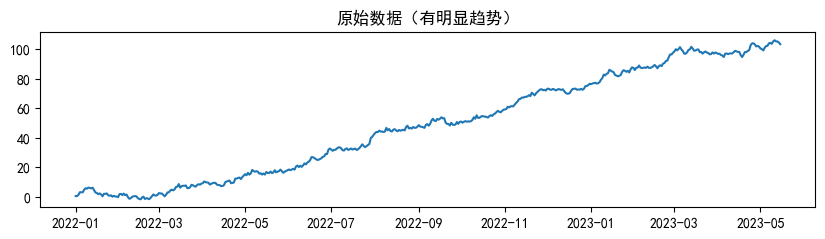
plt.title('原始数据(有明显趋势)')
# ADF检验
adf_result_original = adfuller(data)
print(f'原始数据的ADF检验结果:')
print(f' ADF Statistic: {adf_result_original[0]}') # 0.1357836533616823
print(f' p-value: {adf_result_original[1]}') # 0.9684209812957272,说明是非平稳的
# 3. 进行一阶差分治疗
data_diff = data.diff().dropna() # .diff()进行差分, .dropna()移除第一个NaN值(第一个元素没有值可减)
plt.plot(data_diff)
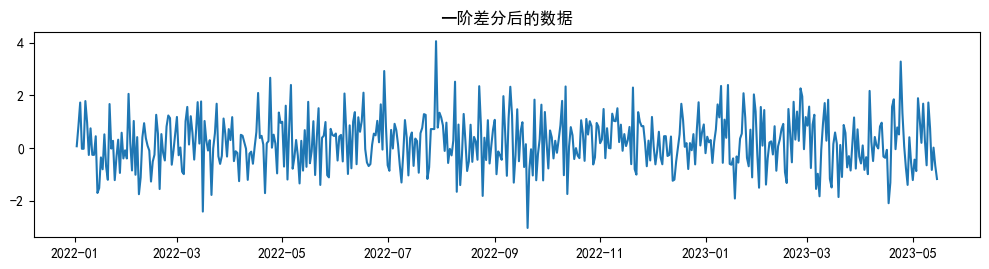
plt.title('一阶差分后的数据')
plt.tight_layout()
plt.show()
# 诊断“治疗后”的数据
adf_result_diff = adfuller(data_diff)
print(f'一阶差分后数据的ADF检验结果:')
print(f' ADF Statistic: {adf_result_diff[0]}') # -22.313025583815016
print(f' p-value: {adf_result_diff[1]}') # 0.0,说明数据变平稳了
一阶差分后,可以发现图像的趋势基本消失,整体在0附近来回波动,变得平稳了。
1.2 季节性
对于季节性来说,它的不稳定性来源于数据以年、季度或月为单位的固定周期性波动。为了消除这一波动,采用的是季节性差分。它本质上也是看数据变化速度,只不过对应的是上一个周期的速度,而非上一个值。
这里使用sin函数模型模拟季节性成分:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
# 1. 生成一段有季节性的数据
# 假设是4年的月度数据,周期为12
time_index = pd.date_range(start='2020-01-01', periods=48, freq='M')
# 季节性成分(用sin函数模拟)
seasonal_component = np.sin(np.arange(48) * (2 * np.pi / 12)) * 10 # 振幅为10,周期为12个月,sin函数模拟季节性波动
# 趋势成分
trend_component = np.linspace(0, 20, 48) # linspace函数为生成0到20的线性趋势,包含48个点
# 随机噪声
noise = np.random.randn(48) * 2
# 合成数据
seasonal_data = pd.Series(seasonal_component + trend_component + noise, index=time_index)整体处理方法同上,只不过加入了周期性(period=12)的处理:每个数据点减去12个月前的值
# 2. 观察原始数据
plt.figure(figsize=(12, 6))
plt.subplot(211)
plt.plot(seasonal_data)
plt.title('原始季节性数据')
# 3. 进行季节性差分(周期s=12)
seasonal_data_diff = seasonal_data.diff(periods=12).dropna()
plt.subplot(212)
plt.plot(seasonal_data_diff)
plt.title('季节性差分后 (s=12) 的数据')
plt.tight_layout()
plt.show()
# 4. 检查差分后的平稳性
# 注意:原始数据因为有趋势,肯定不平稳。季节性差分通常也能消除一部分趋势。
adf_result_original = adfuller(seasonal_data)
print(f'原始季节性数据的p-value: {adf_result_original[1]}') # 0.9918566279818364
adf_result_seasonal_diff = adfuller(seasonal_data_diff)
print(f'季节性差分后数据的p-value: {adf_result_seasonal_diff[1]}') # 4.596236388830458e-12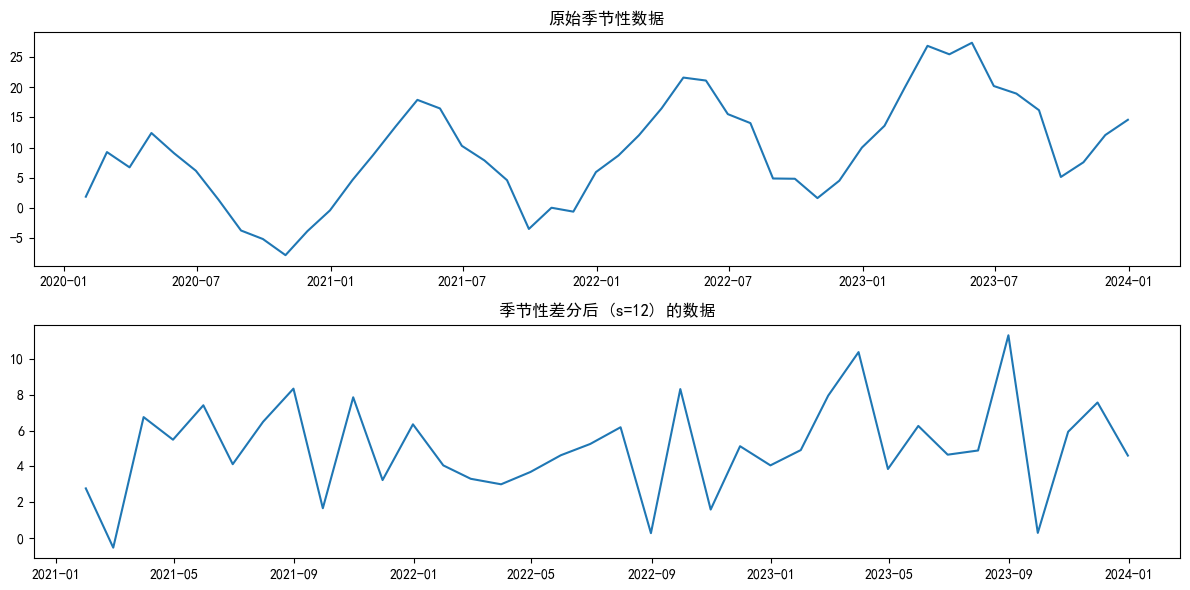
注:数据同时含有趋势和季节性,先处理季节性,再用普通差分处理趋势。因为季节性差分通常也能消除一部分趋势。
二、模型选择
通过处理非平稳性和季节性后,得到了平稳的数据,就可以进入模型选择阶段。模型选择依赖于:
- ACF:衡量一个值和它所有过去值之间的关系,不管这些关系是直接的还是间接的
- PACF:只衡量一个值和它某个过去值之间的直接、纯粹的关系,排除了所有“中间人”的干扰
注:PACF要求,lags ≤ 50% 的样本量
2.1 AR模型:短期预测
AR(Autoregressive Model,自回归模型):当前值依赖于过去观测值的线性组合,再加上随机噪声。它认为时间序列数据具有一种“惯性”或“记忆性”。
AR(p)模型:表示当前值 Xt 只与它过去的 p 个值 (Xt-1, Xt-2, …, Xt-p) 有关。
X(t) = c + φ₁X(t-1) + φ₂X(t-2) + ... + φ_pX(t-p) + ε(t)
其中,X(t):当前时刻的值;c:常数项;φ₁,φ₂, ..., φ_p:自回归系数;X(t-1), ..., X(t-p):历史值;ε(t):白噪声误差项;p:模型阶数。
2.1.1 模型阶数p的选择
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA
# 设置中文字体,防止matplotlib显示乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# --- AR(2) 案例:湖水温度 ---
print("--- 案例一:AR(2)模型 - 湖水温度 ---")
# 1.1 生成AR(2)时间序列数据
# AR(2)模型结构:X_t = 0.7*X_{t-1} + 0.2*X_{t-2} + ε_t
# 其中ε_t是白噪声,系数0.7和0.2控制了前两期对当前值的影响程度
ar_params = np.array([0.7, 0.2]) # AR系数:φ₁=0.7, φ₂=0.2
ma_params = np.array([]) # MA部分为空(纯AR模型)
# 转换为statsmodels要求的格式:
# AR系数需添加首项1并取负,即 [1, -φ₁, -φ₂]
ar_coeffs = np.r_[1, -ar_params] # 生成 [1, -0.7, -0.2]
# MA系数需添加首项1,即 [1, θ₁, θ₂, ...]
ma_coeffs = np.r_[1, ma_params] # 生成 [1.]
# 创建AR(2)过程实例
ar_process = ArmaProcess(ar=ar_coeffs, ma=ma_coeffs)
# 生成500个样本点,模拟500天的湖水温度数据
# 设置随机种子确保结果可复现
np.random.seed(100)
ar_data = ar_process.generate_sample(nsample=500)
# 1.2 时间序列分析的"侦探工作":通过可视化初步诊断模型阶数
fig, axes = plt.subplots(3, 1, figsize=(10, 9))
# 1.2.1 绘制原始时间序列图
axes[0].plot(ar_data)
axes[0].set_title('模拟的湖水温度数据 (AR(2)过程)')
axes[0].set_ylabel('温度值')
# 关键点:观察数据是否具有平稳性特征(均值和方差是否随时间变化)
# 1.2.2 绘制自相关函数(ACF)图 - 衡量序列与其滞后值的相关性
plot_acf(ar_data, ax=axes[1], lags=20, title='自相关函数 (ACF)')
# 关键点:AR(p)模型的ACF会呈现指数衰减或周期性衰减
# 这里我们应该看到ACF在滞后2阶后显著下降
# 1.2.3 绘制偏自相关函数(PACF)图 - 控制了中间滞后项后的相关性
plot_pacf(ar_data, ax=axes[2], lags=20, title='偏自相关函数 (PACF)')
# 关键点:AR(p)模型的PACF会在p阶后截断(变为不显著)
# 这里我们应该看到PACF在滞后2阶后截断,辅助确认p=2
plt.tight_layout()
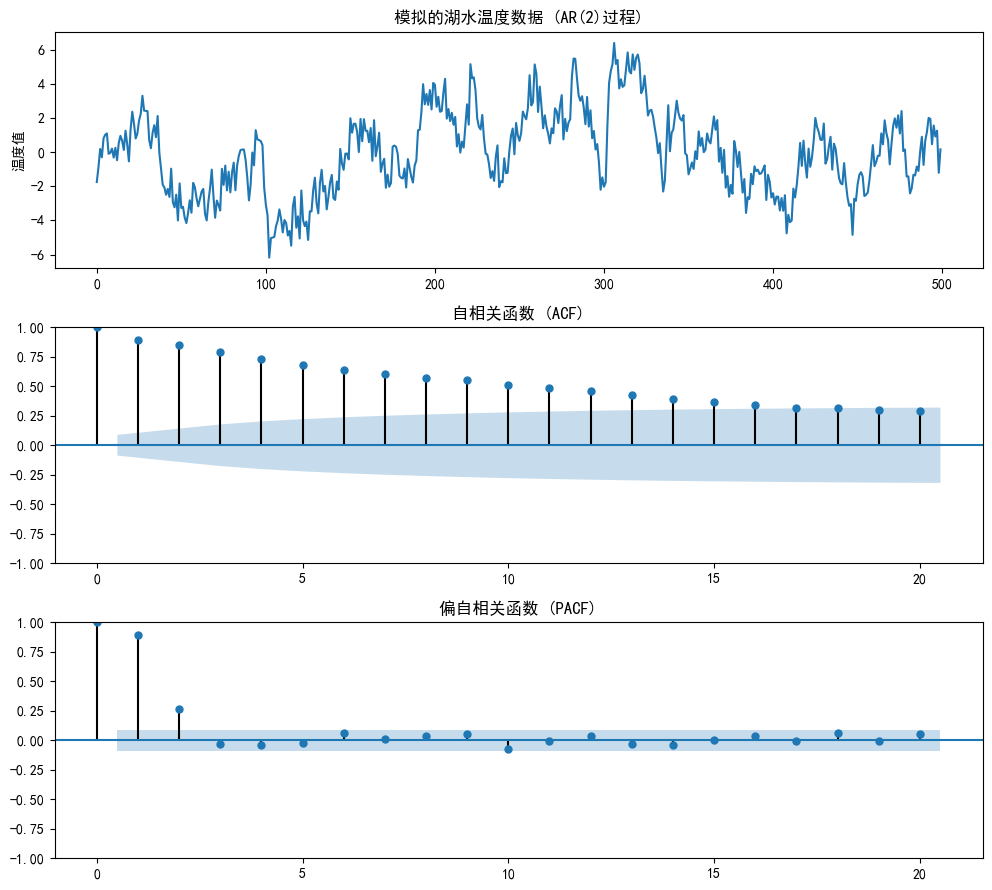
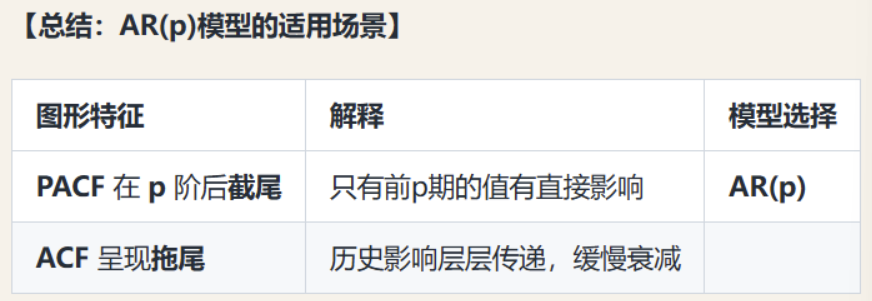
plt.show()选择模型阶数时主要看PACF和ACF:
- PACF出现截尾:关键证据,在延迟p阶后,函数值在某一阶数后突然变为 0(或在置信区间内),且之后几乎不再显著不为 0。
- ACF出现拖尾:辅助,函数值随阶数增加逐渐衰减(如指数衰减、振荡衰减),但始终不降至 0,呈现 “拖曳” 趋势。
2.1.2 模型诊断报告
ARIMA(p,d,q)= AR(自回归)+ I(差分)+ MA(移动平均):
- p = AR模型的阶数:用前p个历史值来预测当前值,PACF
- d = 使序列平稳所需的差分次数:用于去除趋势,使序列平稳
- q = MA模型的阶数:用前q个预测误差来改进预测,ACF
# 1.3 根据ACF/PACF图的诊断,建立ARIMA(2,0,0)模型
model_ar = ARIMA(ar_data, order=(2, 0, 0)).fit()
print("\nAR(2)模型诊断报告:")
print(model_ar.summary())通过诊断报告验证根据PACF的关键特征得到的AR(2):
系数显著:模型准确地识别出前两阶的自回归关系是统计上显著的,并且学习到的系数值(0.66, 0.26)与真实值(0.7, 0.2)非常接近。
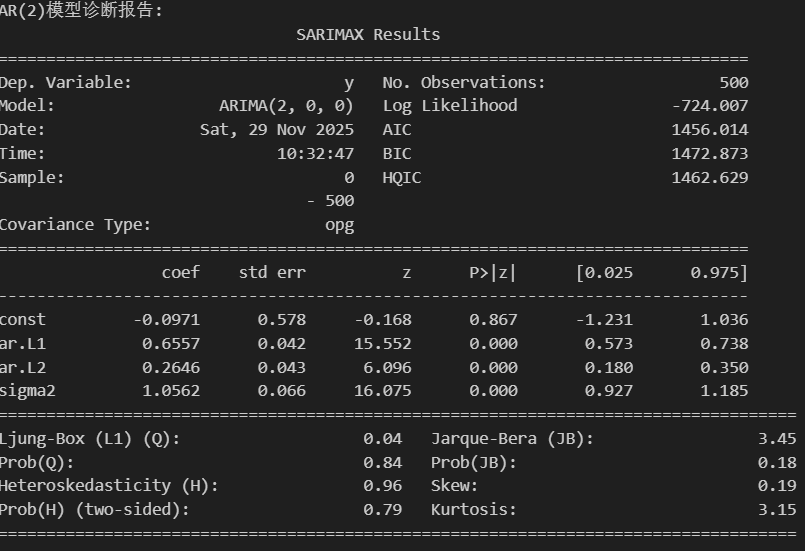
AI 解读的结论:
- 所有AR项高度显著(P值均为0.000)
- 残差为白噪声(Ljung-Box P=0.84)
- 残差近似正态分布(JB P=0.18)
- 无异方差问题(H检验 P=0.79)
-
常数项不显著,可考虑移除简化模型
2.1.3 小结
AR模型适合于短期预测,对于短期依赖关系建模效果好。但是它难以处理非线性、周期性强的数据,并且阶数p的选择对结果影响大。
2.2 MA模型:随机冲击
MA(Moving Average Model,移动平均模型):用过去噪声(冲击)的线性组合来预测当前值。例如假设一条生产线非常稳定,但偶尔会因为工人操作失误或机器小故障(这些都是随机冲击/误差)导致当天的产量出现波动。这个冲击的影响可能只会持续一两天(短期冲击)。
X(t) = μ + ε(t) + θ₁ε(t-1) + θ₂ε(t-2) + ... + θ_qε(t-q)
其中,X(t):当前时刻的值;μ:序列的均值;ε(t),ε(t-1),...,ε(t-q):白噪声误差项;θ₁,θ₂,...,θ_q:移动平均系数;q:模型阶数
2.2.1 模型阶数q
# --- MA(2) 案例:生产线意外 ---
print("\n" + "---"*15)
print("--- 案例二:MA(2)模型 - 生产线意外 ---")
"""
=====================
2.1 生成MA(2)时间序列
=====================
MA(2)模型数学表达式:y_t = ε_t + θ₁ε_{t-1} + θ₂ε_{t-2}
- 当前值由当前及前两期的随机冲击(ε)线性组合而成
- 适用于捕捉短期冲击对序列的影响(如生产线故障、原料短缺)
"""
# AR部分参数:因无自回归项
ar_params = np.array([])
# MA部分参数:0.8和0.4分别是前两期冲击的权重
ma_params = np.array([0.8, 0.4])
# 生成MA(2)过程:直接传入AR和MA系数数组(注意无参数名)
ma_process = ArmaProcess.from_coeffs(ar_params, ma_params)
# 设置随机种子保证结果可复现,生成500个样本点
np.random.seed(200)
ma_data = ma_process.generate_sample(nsample=500)
"""
============================
2.2 可视化分析时间序列特征
============================
通过观察ACF和PACF图判断模型阶数:
- MA(q)模型的ACF应在q阶后截尾(本例q=2)
- PACF应呈现拖尾特征(与AR模型区分)
"""
# 创建3个子图:时间序列图、ACF图、PACF图
fig, axes = plt.subplots(3, 1, figsize=(10, 9))
# 绘制时间序列图:展示生产线产量波动
axes[0].plot(ma_data)
axes[0].set_title('模拟的生产线产量波动 (MA(2)过程)')
axes[0].set_xlabel('时间点')
axes[0].set_ylabel('产量波动值')
# 绘制自相关函数(ACF)图:观察序列相关性衰减模式
plot_acf(ma_data, ax=axes[1], lags=20, title='自相关函数 (ACF)')
# 理论预期:MA(2)的ACF应在2阶后截尾(相关性骤降为0)
# 绘制偏自相关函数(PACF)图:剔除中间变量影响的直接相关性
plot_pacf(ma_data, ax=axes[2], lags=20, title='偏自相关函数 (PACF)')
# 理论预期:MA(2)的PACF应呈现拖尾(指数或振荡衰减)
# 优化子图布局,避免重叠
plt.tight_layout()
plt.show()可以看到在MA模型中,与AR模型不同,ACF在q期后表现出明显的截尾现象(关键),PACF表现出拖尾现象。
t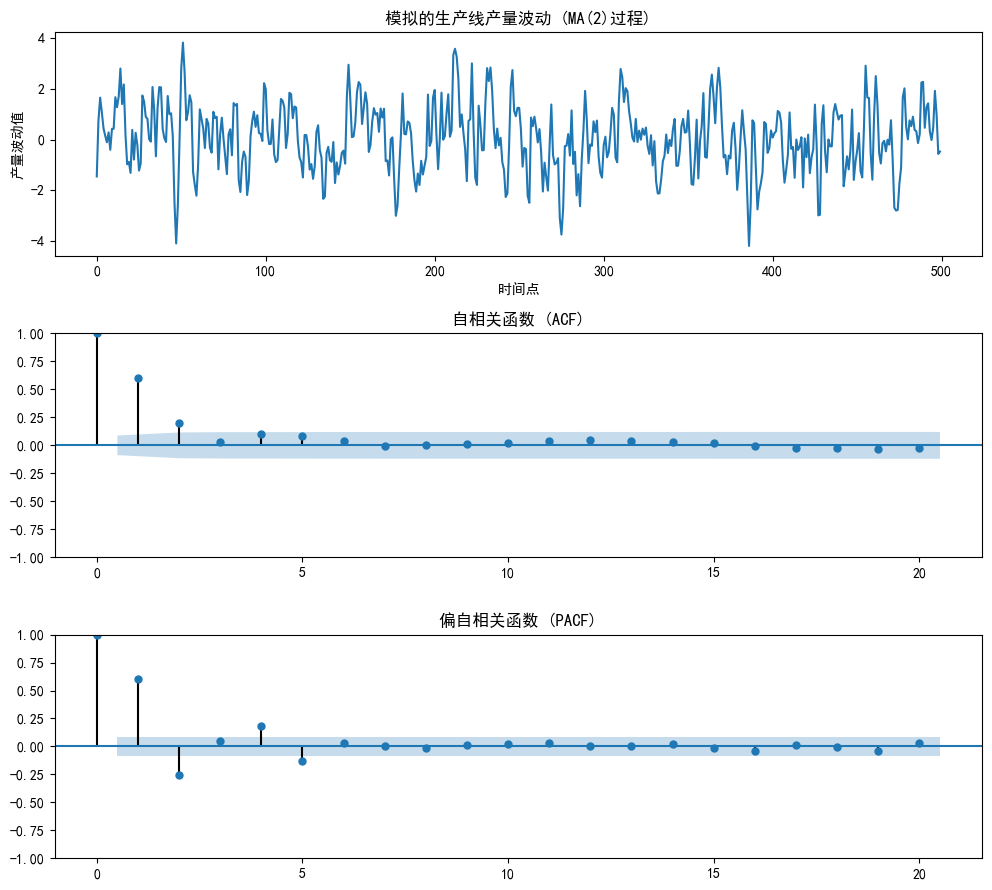
2.2.2 模型诊断报告
# 2.3 根据ACF/PACF图的诊断,建立ARIMA(0,0,2)模型
model_ma = ARIMA(ma_data, order=(0, 0, 2)).fit()
print("\nMA(2)模型诊断报告:")
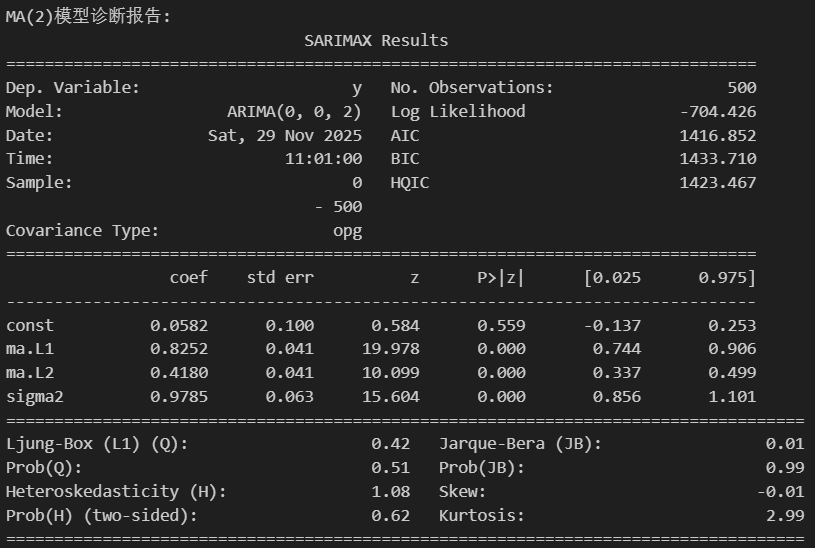
print(model_ma.summary())通过诊断报告验证根据ACF的关键特征得到的MA(2):ma.L1的系数约为0.8,ma.L2的系数约为0.4,和我们设定的参数高度吻合;p值也都极其显著。
2.3 ARMA模型
ARMA(AutoRegressive Moving Average):混合AR和MA,使用AR部分用历史观测值预测当前值,使用MA部分用历史预测误差改进预测。
2.3.1 模型特征
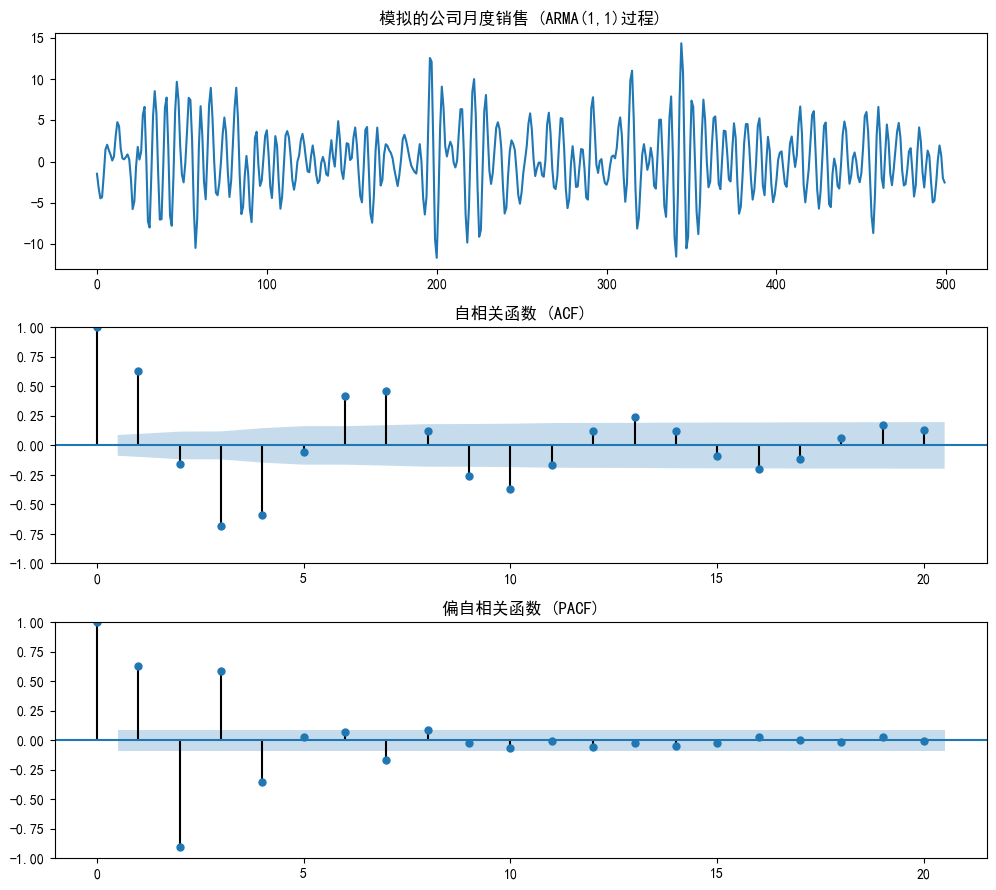
例如:公司月度销售额,既有上个月业绩带来的惯性(AR成分),又会受到某次市场推广活动或负面新闻的短期冲击(MA成分)
# --- ARMA(1,1) 案例:公司月度销售 ---
print("\n" + "---"*15)
print("--- 案例三:ARMA(1,1)模型 - 公司月度销售 ---")
# 3.1 我们来“创造”一个ARMA(1,1)过程
# 修复:直接传入系数数组,并确保包含常数项
ar_params = np.array([1, -0.8]) # AR部分: [1, -φ1]
ma_params = np.array([1, 0.5]) # MA部分: [1, θ1]
# 正确调用方式:直接传入系数数组,不使用参数名
arma_process = ArmaProcess.from_coeffs(ar_params, ma_params)
np.random.seed(300)
arma_data = arma_process.generate_sample(nsample=500)
# 3.2 作为“侦探”,我们观察数据和ACF/PACF图
fig, axes = plt.subplots(3, 1, figsize=(10, 9))
axes[0].plot(arma_data)
axes[0].set_title('模拟的公司月度销售 (ARMA(1,1)过程)')
plot_acf(arma_data, ax=axes[1], lags=20, title='自相关函数 (ACF)')
plot_pacf(arma_data, ax=axes[2], lags=20, title='偏自相关函数 (PACF)')
plt.tight_layout()
plt.show()ACF和PACF均没有明显的截尾现象,两者都呈现拖尾(缓慢衰减)→ 混合驱动力,包含AR和MR
2.3.2 模型判断
对于ARMA模型,从图上直接确定p和q的精确值会比较困难。通常我们会从低阶开始尝试,比如(1,1), (2,1), (1,2),然后结合后续的模型评估指标(如AIC, BIC)来选择最优的。但既然两个图都是拖尾,我们就先从最简单的ARMA(1,1)开始猜起。
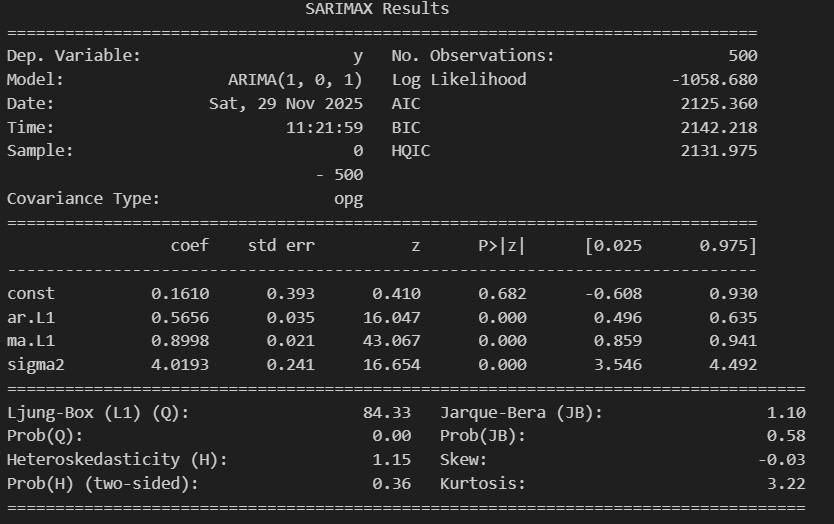
# 3.3 根据ACF/PACF图的诊断,建立ARIMA(1,0,1)模型
model_arma = ARIMA(arma_data, order=(1, 0, 1)).fit()
print("\nARMA(1,1)模型诊断报告:")
print(model_arma.summary())
三、总结
(1)在建模之间,需要保证数据的平稳性。处理方法是差分。
- 非平稳性(趋势):普通差分(.diff())
- 季节性:季节性差分(.diff(periods=s))
- 自相关性:不消除,利用ACF和PACF为模型选择提供线索
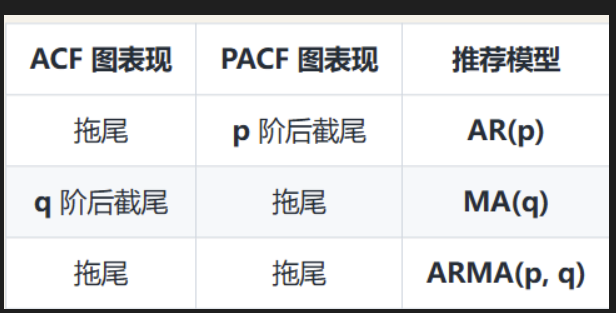
(2)数据平稳后,可以使用PACF和ACF分析,通过查看拖尾和截尾特征,确定模型。
- 截尾:ACF或PACF图在某个延迟之后,相关系数突然变得非常小,几乎都在置信区间内。
- 拖尾:相关系数随着延迟增加而缓慢、指数级地衰减,而不是突然截断。
(3)定阶与诊断:创建ARIMA(p.d,q)模型,通过诊断报告的系数、p值等判断合理性。
- ARMA模型:采用从低阶尝试开始,
- AR模型:PACF的截尾处
- MA模型:ACF的截尾处
四、作业
常见的时序单变量数据集有:
- 洗发水销售数据集:3年期间每月洗发水的销售量
- 每日最低温度数据集:澳大利亚墨尔本市 10 年(1981-1990 年)的最低日温度
- 每月太阳黑子数据集:200多年(1818-2019 年)观测到的太阳黑子数量的月度计数
- 每日女性出生数据集:1959年加利福尼亚州每天的女性出生人数
下面以洗发水销售数据集为例,查看性质:
4.1 平稳性
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# 读取数据
df = pd.read_csv('shampoo-sales.csv')
# 数据预处理 - 创建时间索引
# 将1-01, 1-02等转换为连续的时间序列
df['TimeIndex'] = range(1, len(df) + 1)
# 创建时间序列
time_series = pd.Series(df['Sales'].values, index=df['TimeIndex'])
# 绘制图表
plt.figure(figsize=(12, 9))
# 1-原始数据
plt.subplot(311)
plt.plot(time_series, marker='o', linewidth=2, markersize=4)
plt.title('Shampoo Sales Time Series', fontsize=14, fontweight='bold')
plt.xlabel('Time Period (Months)')
plt.ylabel('Sales')
plt.grid(True, alpha=0.3)
# 2-季节性差分
seasonal_data_diff = time_series.diff(periods=12).dropna()
plt.subplot(312)
plt.plot(seasonal_data_diff,marker='o', linewidth=2, markersize=4)
plt.title('Shampoo Sales Time Series(Seasonal Decomposed)',fontsize=14, fontweight='bold')
plt.xlabel('Time Period (Months)')
plt.ylabel('Sales')
plt.grid(True, alpha=0.3)
# 3-去除趋势
data_diff = seasonal_data_diff.diff().dropna()
plt.subplot(313)
plt.plot(data_diff,marker='o', linewidth=2, markersize=4)
plt.title('Shampoo Sales Time Series(Decomposed)',fontsize=14, fontweight='bold')
plt.xlabel('Time Period (Months)')
plt.ylabel('Sales')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# ADF检验
adf_result_original = adfuller(time_series)
print(f'原始季节性数据的p-value: {adf_result_original[1]}')
adf_result_seasonal_diff = adfuller(seasonal_data_diff)
print(f'季节性差分后数据的p-value: {adf_result_seasonal_diff[1]}')
adf_result_diff = adfuller(data_diff)
print(f'普通差分后数据的p-value: {adf_result_diff[1]}')
原始季节性数据的p-value: 1.0
季节性差分后数据的p-value: 0.9545931714075301
普通差分后数据的p-value: 2.5368941168684403e-08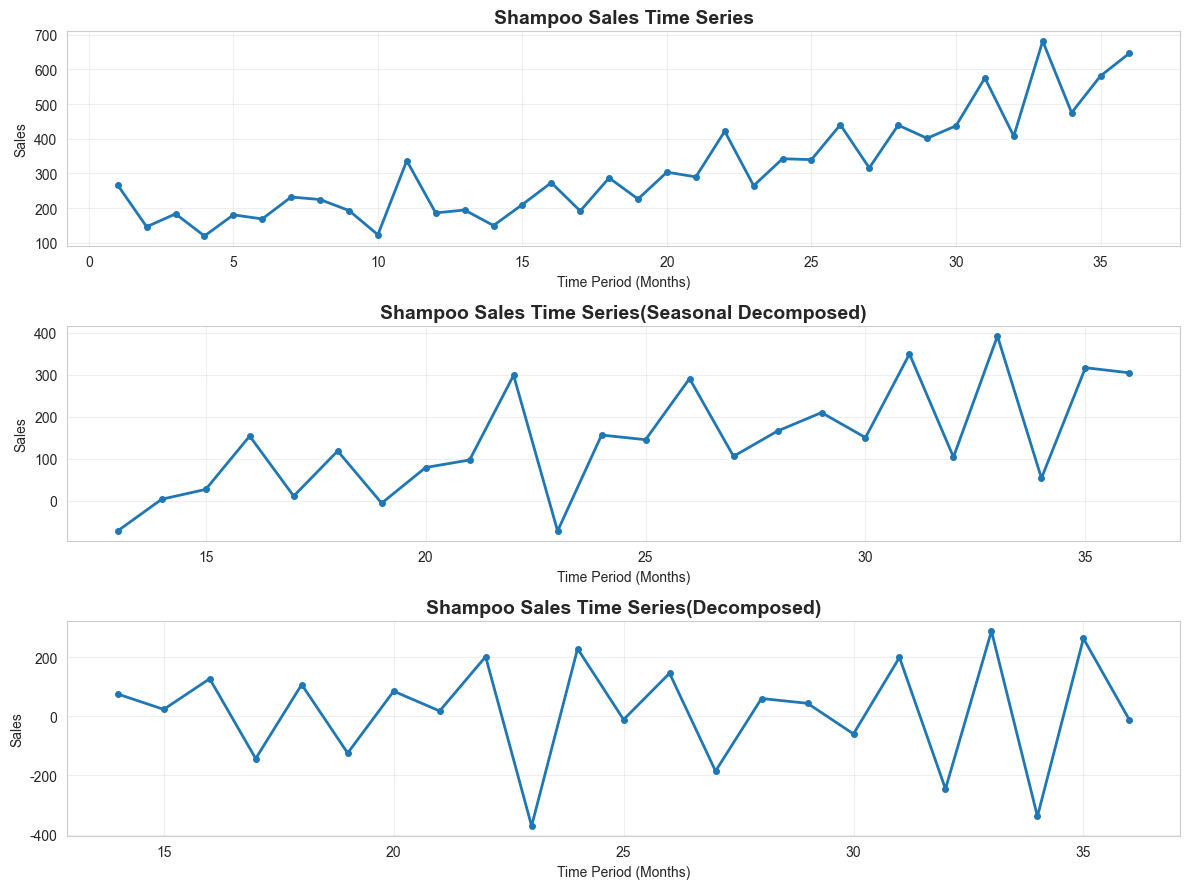
4.2 ACF和PACF查看
fig, axes = plt.subplots(3, 1, figsize=(10, 9))
axes[0].plot(data_diff)
axes[0].set_title('Shampoo Sales Time Series')
plot_acf(data_diff, ax=axes[1], lags=10, title='ACF')
plot_pacf(data_diff, ax=axes[2], lags=10, title='PACF')
plt.tight_layout()
plt.show()受限于样本数量,lag只能设置到10。
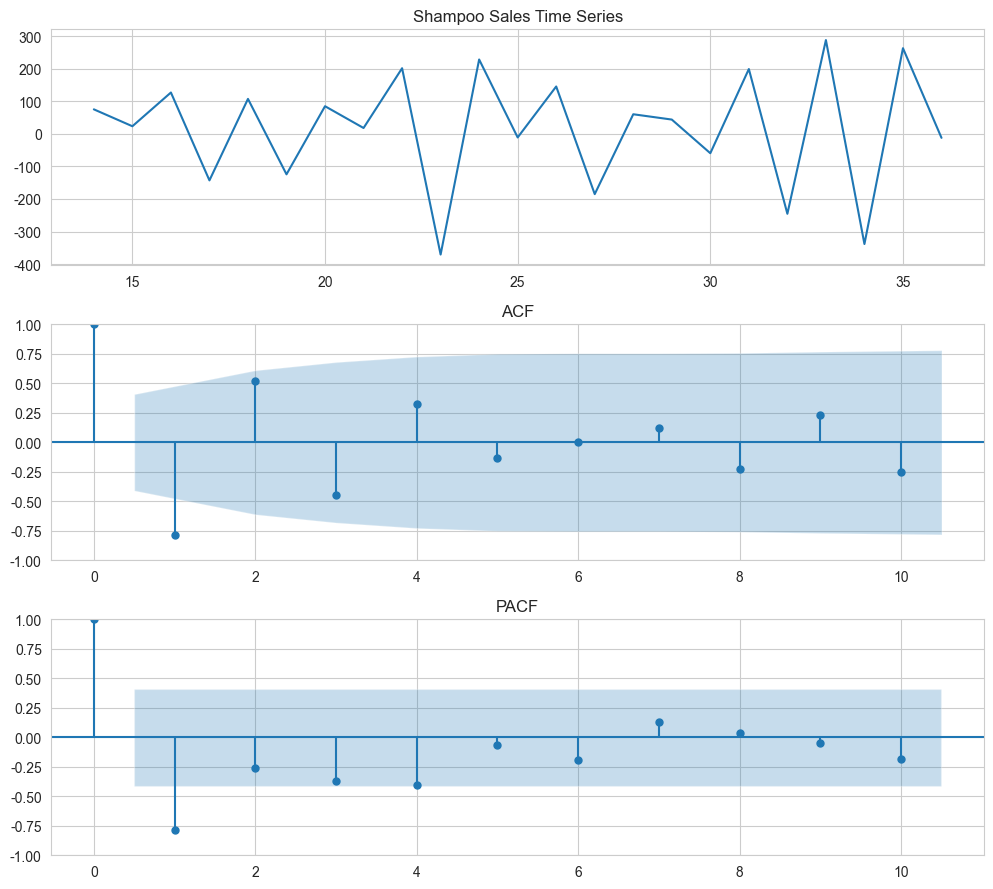
- ACF:总体呈现的是逐渐衰减到0(拖尾)→ q =0(MA成分)
- PACF:存在截尾现象 → p =1 or 2 (AR成分)





















 1008
1008

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








