Day 48 随机函数与广播机制-优快云博客

今日任务：

随机张量的生成：torch.randn函数
卷积和池化的计算公式（可以不掌握，会自动计算的）
pytorch的广播机制：加法和乘法的广播机制（numpy也有广播机制）

作业：自己多借助ai举几个例子帮助自己理解即可

随机张量的生成

用途：权重初始化；计算输入维度经过模块后输出的维度

种类：标准正态分布；[0,1)均匀分布；随机整数；普通正态分布

（1）torch.randn函数：创建一个由标准正态分布（均值为0，标准差为1）随机数填充的张量。参数说明：

import torch
scalar = torch.randn(()) # 标量（0维张量）
vector = torch.randn(5)  # 长度为5的向量（1维）
matrix = torch.randn(3, 4)  # 3行4列的矩阵（2维）
tensor_3d = torch.randn(3, 224, 224)  # 3通道，高224，宽224（3维，[C,H,W]）
tensor_4d = torch.randn(2, 3, 224, 224)  # 批量大小为2，3通道，高224，宽224(4维,[B,C,H,W])
# 可以通过shape属性查看尺寸
print(f"4维张量形状: {tensor_4d.shape}")  # 输出: torch.Size([2, 3, 224, 224])

（2）其它

torch.rand()：生成[0,1)范围内的均匀分布的随机数
torch.randint(low,high,size)：生成指定范围内的随机整数
torch.normal(mean,std)：生成指定均值和标准差的正态分布随机数

# 均匀分布
x = torch.rand(3, 2)  # 生成3x2的张量
# 随机整数
y = torch.randint(low=0, high=10, size=(3,))  # 生成3个0到9之间的整数
# 正态分布
mean = torch.tensor([0.0, 0.0])
std = torch.tensor([1.0, 2.0])
z = torch.normal(mean, std)  # 生成两个正态分布随机数

注：掌握其中一种方法即可，因为主要目的是生成随机张量，与分布种类无关

输出维度测试

在运行的时候，可以先随机生成张量（4D）模拟图片加载，查看输出维度的变化，避免输入实际数据时报错。

卷积和池化

两者计算输出尺寸的公式相同：

$out\underline{~}size=\frac{input\underline{~}size+2\times padding-kernel\underline{~}size}{stride}+1$

其中，out_size为输出尺寸，input_size为输入尺寸，padding为填充，kernel_size为卷积核大小，stride为步长。

例子：

# 1. 卷积层操作
conv1 = nn.Conv2d(
    in_channels=3,        # 输入通道数
    out_channels=16,      # 输出通道数（卷积核数量）
    kernel_size=3,        # 卷积核大小
    stride=1,             # 步长
    padding=1             # 填充
)
conv_output = conv1(input_tensor) # 由于 padding=1 且 stride=1，空间尺寸保持不变
# 计算：(32 + 2*1 - 3) / 1 + 1 = 32
print(f"卷积后尺寸: {conv_output.shape}")  # 输出: [1, 16, 32, 32]

# 2. 池化层操作 (减小空间尺寸)
pool = nn.MaxPool2d(kernel_size=2, stride=2) # 创建一个最大池化层
pool_output = pool(conv_output)
# 计算：(32 + 2*0 - 2) / 2 + 1 = 16
print(f"池化后尺寸: {pool_output.shape}")  # 输出: [1, 16, 16, 16]

全连接层（分类器）

输入为一维张量[batch,input]，输出也为一维张量[batch,out]

注意：

shape查看完整尺寸信息；size(dim)查看具体维度的尺寸。x.shape[1] == x.size(1)
多分类问题通常使用softmax，二分类使用sigmoid。

# 3. 将多维张量展平为向量
flattened = pool_output.view(pool_output.size(0), -1) # -1为自动计算维度
print(f"展平后尺寸: {flattened.shape}")  # 输出: [1, 4096] (16*16*16=4096)
# 4. 线性层操作
fc1 = nn.Linear(
    in_features=4096,     # 输入特征数
    out_features=128      # 输出特征数
)
fc_output = fc1(flattened)
print(f"线性层后尺寸: {fc_output.shape}")  # 输出: [1, 128]
# 4. 线性层操作
fc1 = nn.Linear(
    in_features=4096,     # 输入特征数
    out_features=128      # 输出特征数
)
fc_output = fc1(flattened)
print(f"线性层后尺寸: {fc_output.shape}")  # 输出: [1, 128]

# 使用Softmax替代Sigmoid
softmax = nn.Softmax(dim=1)  # 在类别维度上进行Softmax
class_probs = softmax(final_output)
print(f"Softmax输出: {class_probs}")  # 总和为1的概率分布
print(f"Softmax输出总和: {class_probs.sum():.4f}")

pytorch的广播机制

广播机制允许在不同形状的张量之间进行算术运算，自动调整张量维度，而无需显式地扩展张量维度或复制数据。

核心：3 条规则

当对两个形状不同的张量进行运算时，PyTorch 会按以下规则自动处理维度兼容性：

（1）从右向左比较维度：PyTorch 从张量的最后一个维度（最右侧）开始向前逐维比较。

（2）维度扩展条件：

相等维度：若两个张量在某一维度上大小相同，则继续比较下一维度。
一维扩展：若其中一个张量在某一维度上大小为1，则该维度会被扩展为另一个张量对应维度的大小。
不兼容错误：若某一维度大小既不相同也不为 1，则抛出 RuntimeError。-----维度必须满足广播规则，否则会报错。

（3）维度补全规则：若一个张量的维度少于另一个，则在其左侧补 1 直至维度数匹配。

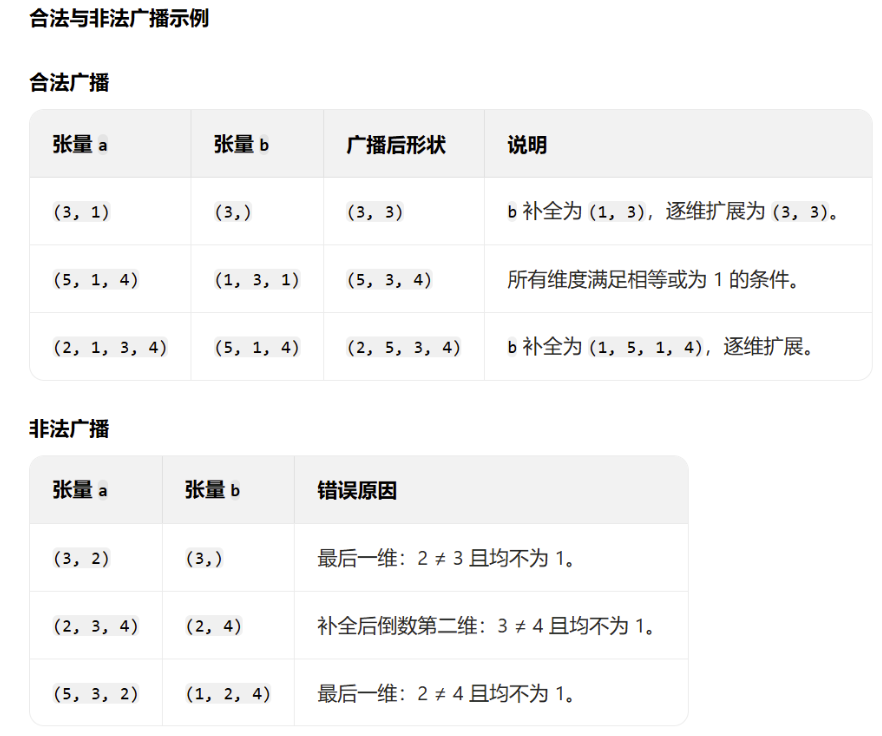
加法

尺寸变化：广播后的形状由各维度的最大值决定（示例 2 中最终形状为 (2, 2, 2)）。
值扩展：维度为 1 的张量通过复制扩展值（b 从 [10, 20] 扩展为两行相同的值）
内存效率：扩展是逻辑上的，实际未复制数据，避免了内存浪费。

# 创建原始张量
a = torch.tensor([[[1], [2]], [[3], [4]]])  # 形状: (2, 2, 1)
b = torch.tensor([[10, 20]])               # 形状: (1, 2)

# 广播过程
# 1. b补全维度: (1, 2) → (1, 1, 2)
# 2. a扩展第三维: (2, 2, 1) → (2, 2, 2)
# 3. b扩展第一维: (1, 1, 2) → (2, 1, 2)
# 4. b扩展第二维: (2, 1, 2) → (2, 2, 2)
# 最终形状: (2, 2, 2)

result = a + b
print("原始张量a:")
print(a)
print("\n原始张量b:")
print(b)


print("\n广播后a的值扩展:")
print(torch.tensor([[[1, 1],
                     [2, 2]],
                    [[3, 3],
                     [4, 4]]]))  # 实际内存中未复制，仅逻辑上扩展

print("\n广播后b的值扩展:")
print(torch.tensor([[[10, 20],
                     [10, 20]],
                    [[10, 20],
                     [10, 20]]]))  # 实际内存中未复制，仅逻辑上扩展

print("\n加法结果:")
print(result)

乘法

矩阵乘法（@）的规则：

最后两个维度：A.shape[-1] == B.shape[-2] , A的列数等于B的行数。
其它维度：通用广播规则，向右对齐维度；维度相同或为1；维度补全

A@B的输出形状：其它维度（两者间的最大值），最后两个维度（A的行数与B的列数）

# A: 批量大小为2，通道数为3，每个是4×5的矩阵
A = torch.randn(2, 3, 4, 5)  # 形状: (2, 3, 4, 5)

# B: 单个5×6的矩阵
B = torch.randn(5, 6)        # 形状: (5, 6)

# 广播过程：
# 1. B补全维度: (5, 6) → (1, 1, 5, 6)
# 2. B扩展第一维: (1, 1, 5, 6) → (2, 1, 5, 6)
# 3. B扩展第二维: (2, 1, 5, 6) → (2, 3, 5, 6)
# 矩阵乘法: (2, 3, 4, 5) @ (2, 3, 5, 6) → (2, 3, 4, 6)
result = A @ B               # 结果形状: (2, 3, 4, 6)

print("A形状:", A.shape)     # 输出: torch.Size([2, 3, 4, 5])
print("B形状:", B.shape)     # 输出: torch.Size([5, 6])
print("结果形状:", result.shape)  # 输出: torch.Size([2, 3, 4, 6])