目录
1、分布函数
分布函数 显示了随机变量的取值落在某个区间上的概率,是一种不减函数。
设 X 是一个随机变量,x 是任意实数,函数
![]()
成为 X 的分布函数。分布函数是一个普通函数,其定义域是整个实数轴。在几何上他表示随机变量 X 落在实数 x 及x 左边的概率,因此落点在 x1 与 x2之间的概率可由 F(x2)-F(x1) 得出。他的取值范围为 [0,1],并且是一个不减函数。易知对于离散随机变量来说,F(x)呈阶梯状。
2、概率密度函数
概率密度函数 f(x) 表示的是随机变量 X 在点 x 的概率分布密集程度,反映出 随机变量X 取 x 附近的值的概率大小。其与概率分布函数的关系如下:

即 F(x) 与 f(x) 互为积分与导数的关系。并且满足:

如正态分布的概率密度函数为:

当![]() ,
,![]() 时就是标准正态分布:
时就是标准正态分布:
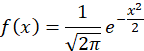





 本文探讨了随机变量的分布函数,解释了它如何表示随机变量落在特定区间内的概率,并介绍了与概率密度函数的关系。重点讲解了正态分布的概率密度函数实例。同时,概述了两者作为导数和积分的对应关系。
本文探讨了随机变量的分布函数,解释了它如何表示随机变量落在特定区间内的概率,并介绍了与概率密度函数的关系。重点讲解了正态分布的概率密度函数实例。同时,概述了两者作为导数和积分的对应关系。

















 1915
1915

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










