先验概率、后验概率及贝叶斯公式的理解

目录

1、条件概率

2、全概率公式

3、先验概率

4、后验概率

5、贝叶斯（bayes）公式

---

介绍这些概念之前，首先需要了解 条件概率 及 全概率公式 。

1、条件概率

在事件 B 发生的条件下事件 A 发生的概率。

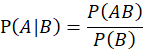
P(AB) 为 A、B 同时发生的概率，在独立同分布的情况下 P(AB)=P(A)P(B)。

2、全概率公式

假如事情 A 的发生可能有 B1、B2… 多种原因导致，则

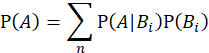
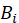 为试验 E 样本空间的一个划分，A 为试验 E 的事件。

3、先验概率

根据以往经验或数据分析得到的已知（原因、类别、途径等的）概率。

4、后验概率

若先验概率为 P(A) ，则称 P(A|b) 为后验概率，即得到 b 的信息之后计算得出的概率，判断结果（b）的发生是由哪个原因（A）引起的概率。后验概率有点事后诸葛亮的意思，就是事情发生后我再去找导致这个事件的原因。

5、贝叶斯（bayes）公式

贝叶斯公式就是用来计算后验概率的一种方式，公式如下

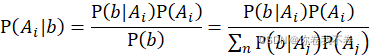
贝叶斯公式主要用于当观察到一个事件（b）已经发生时，去求导致该事件发生的各种原因、情况、途径或事件的种类的可能性大小。公式中使用的 P(b|A) 称作类条件概率，即由原因得到某件事情可能发生的概率。

例如，在机器学习领域中，若 b 是一张图片，把 b 作为网络的输入，则后验概率 P(A|b) 可以作为 b 属于类别 A 的概率。