【顶刊复现】配电网两阶段鲁棒故障恢复研究（Matlab代码实现)

最新推荐文章于 2025-12-13 20:45:00 发布

原创最新推荐文章于 2025-12-13 20:45:00 发布 · 874 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言 #支持向量机

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文内容如下：🎁🎁🎁

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

配电网两阶段鲁棒故障恢复研究文档复现（基于X. Chen等2016年IEEE TPWRS论文）

一、研究背景与核心贡献

问题背景
主动配电网（ADN）中分布式电源（DG）的间歇性、负荷波动性及量测误差导致恢复策略存在不确定性风险。传统确定性模型在极端场景下易出现恢复失败或约束违反（如分支过载、电压越限）。
核心贡献
- 提出两阶段鲁棒优化模型（RROM），第一阶段生成最优恢复策略，第二阶段搜索最恶劣波动场景。
- 引入不确定性预算技术，平衡模型保守性与优化性能。
- 通过混合整数线性规划（MILP）形式化描述问题，采用列约束生成（C&CG）算法求解。
- 在PG&E 69节点和修改后的246节点系统中验证模型有效性，鲁棒策略在所有测试场景下均保证可行性，而确定性模型在30%场景下失败。

二、模型与方法

两阶段鲁棒优化框架
- 第一阶段（恢复策略生成）：
  目标函数：最大化恢复负荷量，考虑负荷优先级权重。
  约束条件：辐射状拓扑约束、功率平衡约束、线路容量约束、节点电压约束、DG出力约束。
- 第二阶段（最恶劣场景搜索）：
  在给定恢复策略下，寻找使系统运行约束最紧张的DG出力和负荷波动场景。
  目标函数：最小化系统剩余容量裕度（即最大化约束违反风险）。
不确定性建模
- 不确定性集合：基于历史数据构建DG出力和负荷的区间边界，采用盒式不确定性集描述波动范围。
- 不确定性预算：通过调节全局波动范围参数（Γ），控制模型保守性。Γ=0时退化为确定性模型，Γ增大时模型更鲁棒但可能过度保守。
求解算法
- 列约束生成（C&CG）算法：
  1. 初始化：生成初始恢复策略及最恶劣场景。
  2. 迭代求解：交替求解主问题（优化恢复策略）和子问题（搜索最恶劣场景），逐步收敛至最优鲁棒解。
  3. 终止条件：主问题与子问题目标函数差值小于阈值。

三、案例验证与结果分析

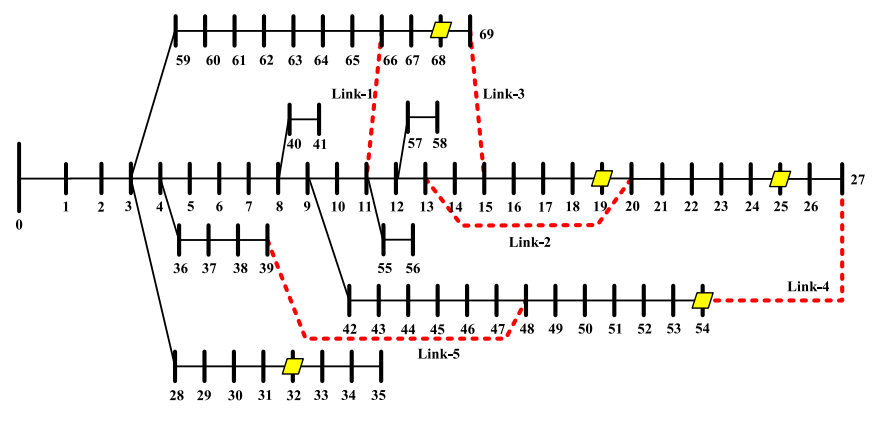
测试系统
- PG&E 69节点系统：含5台DG，总装机容量2.5MW。
- 修改后的246节点系统：模拟高渗透率DG场景，验证模型扩展性。
对比实验
- 确定性模型（DROM）：忽略不确定性，直接优化恢复策略。
- 鲁棒模型（RROM）：考虑不确定性，生成保守但可行的策略。
- 评价指标：恢复成功率、恢复负荷量、计算时间。
关键结果
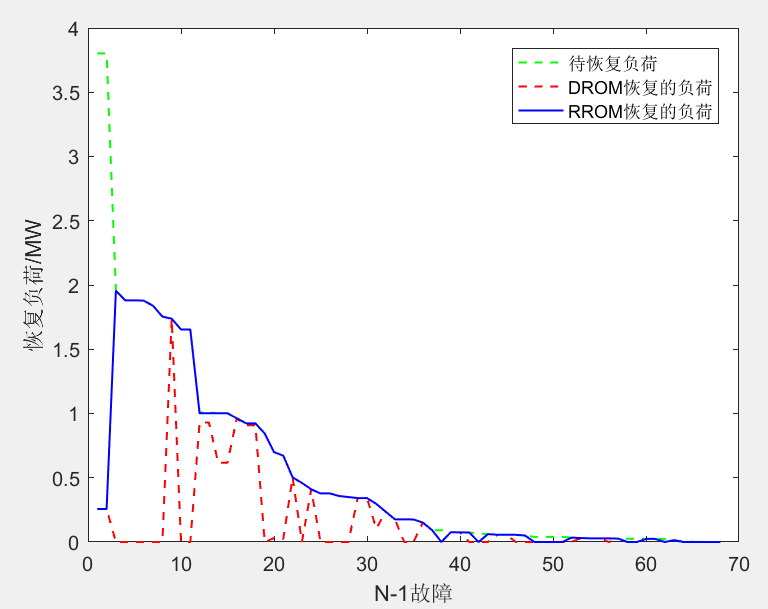
- 最恶劣场景测试：
  - DROM在“N-1”故障扫描中，15%线路故障导致恢复失败（需额外切负荷）。
  - RROM在所有故障下均保证决策可行性，恢复负荷量与DROM接近（差距<5%）。
- 蒙特卡洛仿真：
  - 对3000个随机波动场景测试，RROM恢复成功率100%，DROM在23%场景下失败。
  - RROM计算时间较DROM增加约30%，但仍在可接受范围内（<5分钟）。

四、技术实现与代码复现

代码框架
- 主程序：调用YALMIP工具箱构建优化模型，使用CPLEX求解器。
- 模块划分：
  - data_input.m：加载系统参数（线路阻抗、节点负荷、DG位置等）。
  - uncertainty_set.m：构建DG出力和负荷的波动区间。
  - master_problem.m：求解主问题，生成恢复策略。
  - sub_problem.m：求解子问题，搜索最恶劣场景。
  - CCG_algorithm.m：实现列约束生成迭代流程。

关键代码片段

matlab

% 主问题：优化恢复策略

[x_opt, obj_val] = optimize(MasterProblem, options);

% 子问题：搜索最恶劣场景

[u_opt, worst_case_obj] = optimize(SubProblem(x_opt), options);

% C&CG迭代

while (gap > tolerance)

AddConstraintsToMaster(u_opt); % 将最恶劣场景约束加入主问题

[x_new, obj_new] = optimize(MasterProblem, options);

[u_new, worst_case_new] = optimize(SubProblem(x_new), options);

gap = abs(obj_new - worst_case_new);

end

复现结果验证
- 参数设置：不确定性预算Γ=0.5，波动范围±20%。
- 输出结果：
  - 恢复策略：开关状态、DG出力、负荷恢复量。
  - 最恶劣场景：DG出力和负荷的具体波动值。
  - 收敛曲线：主问题与子问题目标函数随迭代次数的变化。

五、应用价值与扩展方向

实际应用价值
- 提升配电网在极端天气、设备故障等场景下的自愈能力。
- 为调度员提供可执行的恢复策略，减少人工干预。
- 适用于高渗透率DG的主动配电网，支撑新能源消纳。
未来扩展方向
- 多时间尺度优化：结合日前计划与实时调度，提升模型动态适应性。
- 考虑网络重构成本：在目标函数中引入开关操作次数约束，避免频繁拓扑变化。
- 与机器学习结合：利用历史数据训练不确定性预测模型，进一步缩小不确定性集范围。

📚2 运行结果

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

[1] X. Chen, W. Wu and B. Zhang, "Robust Restoration Method for Active Distribution Networks," in IEEE Transactions on Power Systems, vol. 31, no. 5, pp. 4005-4015, Sept. 2016, doi: 10.1109/TPWRS.2015.2503426.