💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
💥1 概述
文章来源:

本文深入剖析并严谨论证了当前应用广泛的ST约束,实则为辐射状拓扑结构成立的必要条件,但并非充分条件,同时给出了确保该约束有效性的辅助条件。在此基础上,本文创新性地提出了基于断线解环理念的辐射状拓扑约束体系,并成功证明了这一组约束条件是保障辐射状网络形成的充分且必要条件。进一步地,依托本文所提出的约束条件,构建了针对配电系统扩建规划及故障恢复问题的混合整数凸优化模型。通过配电系统实例验证发现,传统的ST约束无法有效保证辐射状拓扑的生成,而本文所提出的辐射状拓扑约束不仅能确保生成最优的辐射状拓扑结构,且在计算效率上显著优于基于虚拟潮流的SCF0约束。
近年来,随着凸优化理论的不断发展和应用,很多学者采用数学规划方法解决配电网中的优化问
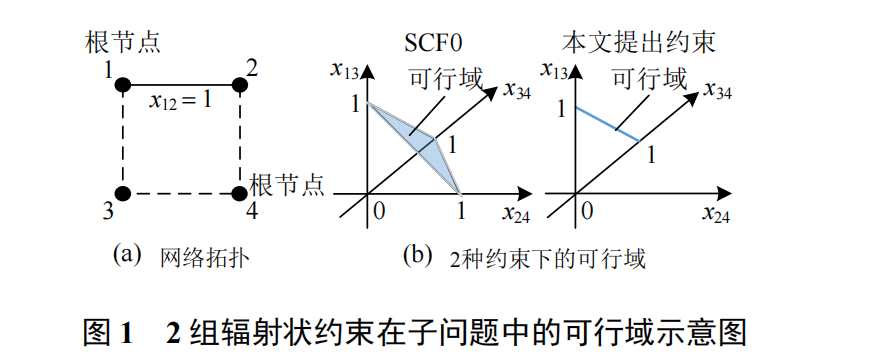
题[1-5]。使用数学规划方法的优势在于,只要将问题建模为凸优化模型或某些特定形式的混合整数凸优化模型,则可利用成熟的商业优化求解器求解并得到全局最优解。在数学规划模型中,约束条件都应是解析表达式,因此对于需要辐射状拓扑的优化问题,需要建立辐射状拓扑约束的数学模型,以确保最终得到的网络为辐射状。文献[6]提出配电系统重构问题的凸优化模型,其中表示辐射状拓扑约束的生成树约束(spanning tree constraints,ST)被广泛应用于其他研究中。文献[7]提出含 ST 约束的交流最优潮流问题的混合整数线性规划模型。文献[8-9]均提出配电网故障恢复问题的混合整数二阶锥规划模型,且其中辐射状约束为 ST 约束。文献[10]利用ST 约束作为辐射状拓扑约束,建立配电网恢复操作次序确定问题的混合整数线性规划模型;文献[11]建立了含 ST 约束的配电网重构和无功优化协调优化问题的混合整数半定规划模型。上述文献均采用ST 约束表示配电网辐射状拓扑约束。然而在大量测试的基础上,笔者发现 ST 约束在某些场景下无法保证得到的拓扑为辐射状。此外文献[12]亦给出了 ST 约束可能会得到含环的非连通图的算例,但该文献并未详细分析 ST 约束无法确保辐射状的原因及相关条件。文献[13]中提到,由于优化问题中潮流约束的存在,使得 ST 约束在某些条件下成立,但未明确给出在何种条件下潮流约束能够使其成立。对于辐射状拓扑建模,除 ST 约束外,文献[14]指出了满足辐射状约束的充分必要条件,即需要同时满足连通性和节点–边的数目关系,并从虚拟潮流的角度提出了确保图的连通性的单商品流约束 (single-commodity flow constraints,SCF),与节点–边的数目关系共同组成辐射状约束(文中记作 SCF0),被应用于相关研究中[13,15]。然而该组约束中仅用 1 个等式描述图中各个边的关系,包含表征线路状态变量的相关信息较少,可能导致混合整数规划求解过程较慢。
基于断线解环思想的配电网辐射状拓扑约束建模方法研究是配电网优化领域的核心问题之一。以下从理论基础、方法创新、数学模型、应用案例及对比分析等方面进行详细阐述:
一、断线解环思想的定义与理论基础
断线解环思想源于电力系统对闭环设计但开环运行的需求。其核心在于通过断开环网中的特定支路,消除网络中的环路,确保配电网呈辐射状运行。具体而言:
- 基本原理:在交流配电网中,所有环路必须满足“至少一条支路断开”的条件,从而破坏环路的闭合性。对于多源系统,还需确保不同根节点之间不存在连通路径,即所有根节点对间的路径也需断开至少一条支路。
- 必要性:传统配电网采用闭环设计以提高灵活性,但开环运行可限制短路电流并控制故障范围。断线解环通过数学建模实现这一物理要求的解析表达。
二、配电网辐射状拓扑结构的特点
辐射状拓扑是配电网运行的典型特征,其特点包括:
- 结构特性:呈树状分布,无闭合环路;节点与支路满足“节点数=支路数+根节点数”的关系。
- 优势与局限:
- 优点:结构简单、经济性高、易于维护,适合开环运行。
- 缺点:单电源供电导致可靠性较低,故障时影响范围大。
- 交直流混合系统:直流配电网可闭环运行,仅交流部分需满足辐射状约束。
三、传统拓扑约束方法的局限性
- 生成树约束(ST):
- 数学表达:通过约束每个节点仅有一条父支路(βfl+βbl≤1βfl+βbl≤1)确保树状结构。
- 不足:仅为辐射状的必要条件,无法避免非连通图或含环子图。
- 单商品流约束(SCF):
- 改进:通过虚拟潮流模型确保连通性,是充分必要条件。
- 局限:引入大量辅助变量,计算复杂度高。
四、基于断线解环思想的建模方法
1. 约束条件设计
该方法通过以下三组约束确保辐射状拓扑:
2. 数学证明
- 充分必要性:上述三组约束联合作用可严格保证网络为连通且无环的辐射状结构,已被证明是充要条件。
- 优势:相比ST和SCF,约束条件更简洁,且无需引入辅助变量。
五、应用案例:扩建规划与故障恢复
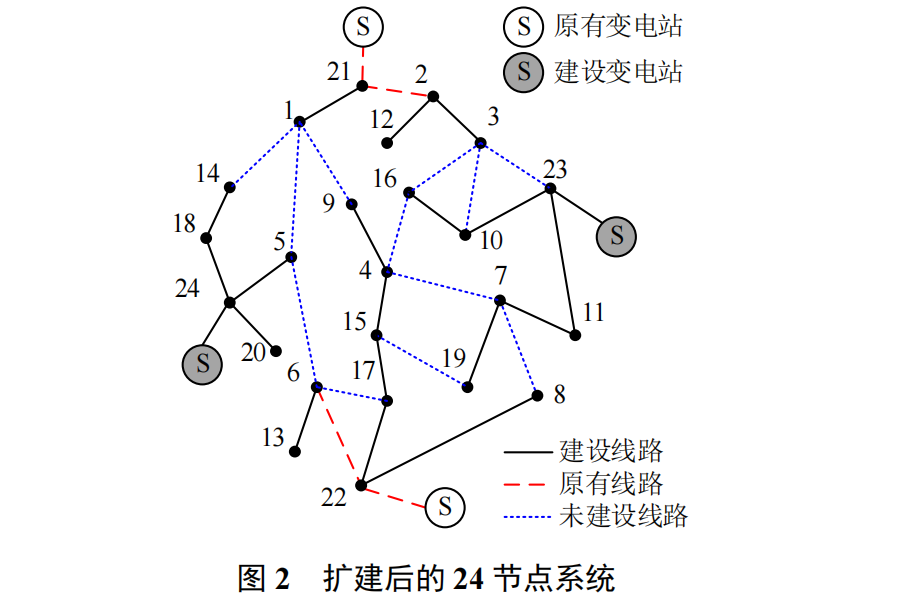
1. 配电系统扩建规划
- 目标函数:最小化投资成本(线路与变电站建设)与运行损耗。
- 约束条件:
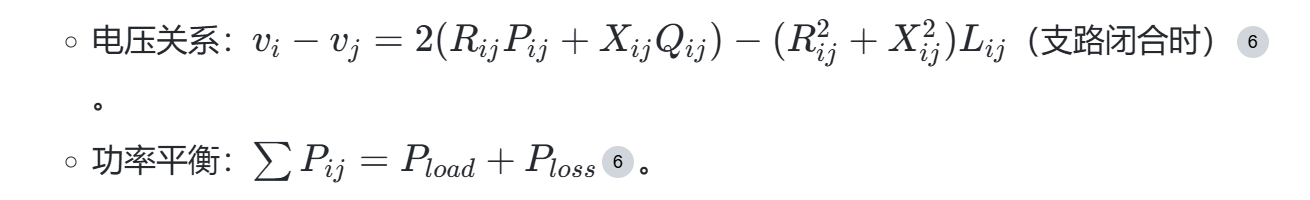
- 拓扑约束:整合断线解环三组约束与变电站连通性条件。
- 求解方法:构建混合整数二阶锥规划(MISOCP)模型,采用MOSEK或Gurobi求解。
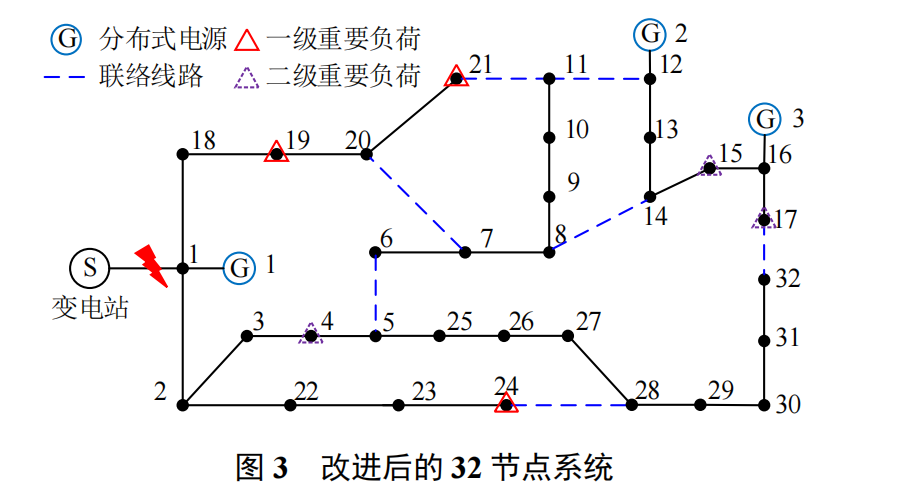
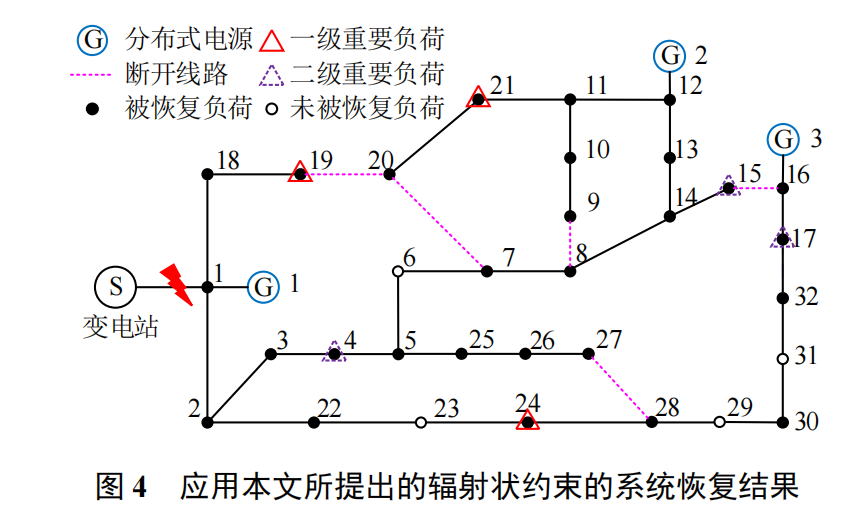
2. 故障恢复问题
- 目标函数:最大化加权负荷恢复量,最小化网损。
- 约束简化:多源场景下仅需环路破坏与节点-边关系约束。
- 算例验证:在改进IEEE33节点系统中,断线解环模型较ST约束减少10%的计算时间,且无拓扑错误。
六、与传统方法的对比分析
| 方法 | 生成树约束(ST) | 单商品流约束(SCF) | 断线解环约束 |
|---|---|---|---|
| 约束性质 | 必要不充分 | 充分必要 | 充分必要 |
| 变量数量 | 中等(节点级约束) | 高(引入虚拟流变量) | 低(仅支路状态变量) |
| 计算效率 | 一般 | 较低 | 较高 |
| 适用场景 | 简单单源网络 | 多源复杂网络 | 交直流混合系统 |
| 典型应用 | 早期文献模型 | 故障恢复优化 | 扩建规划 |
七、未来研究方向
- 多时间尺度优化:结合动态拓扑调整与分布式电源出力波动。
- 数据驱动建模:利用机器学习处理极端运行场景下的拓扑约束。
- 高渗透率可再生能源:研究光储系统接入对辐射状拓扑稳定性的影响。
结论
基于断线解环思想的辐射状拓扑约束建模方法,通过严格的数学定义与优化模型设计,解决了传统方法的不足,在计算效率与可靠性上表现优越。其在扩建规划、故障恢复及交直流混合系统中的应用已验证其工程价值,为智能配电网的优化提供了新的理论工具。未来结合数据驱动与多能源协同优化,将进一步推动该领域的发展。
📚2 运行结果
2.1 配电网拓展规划问题
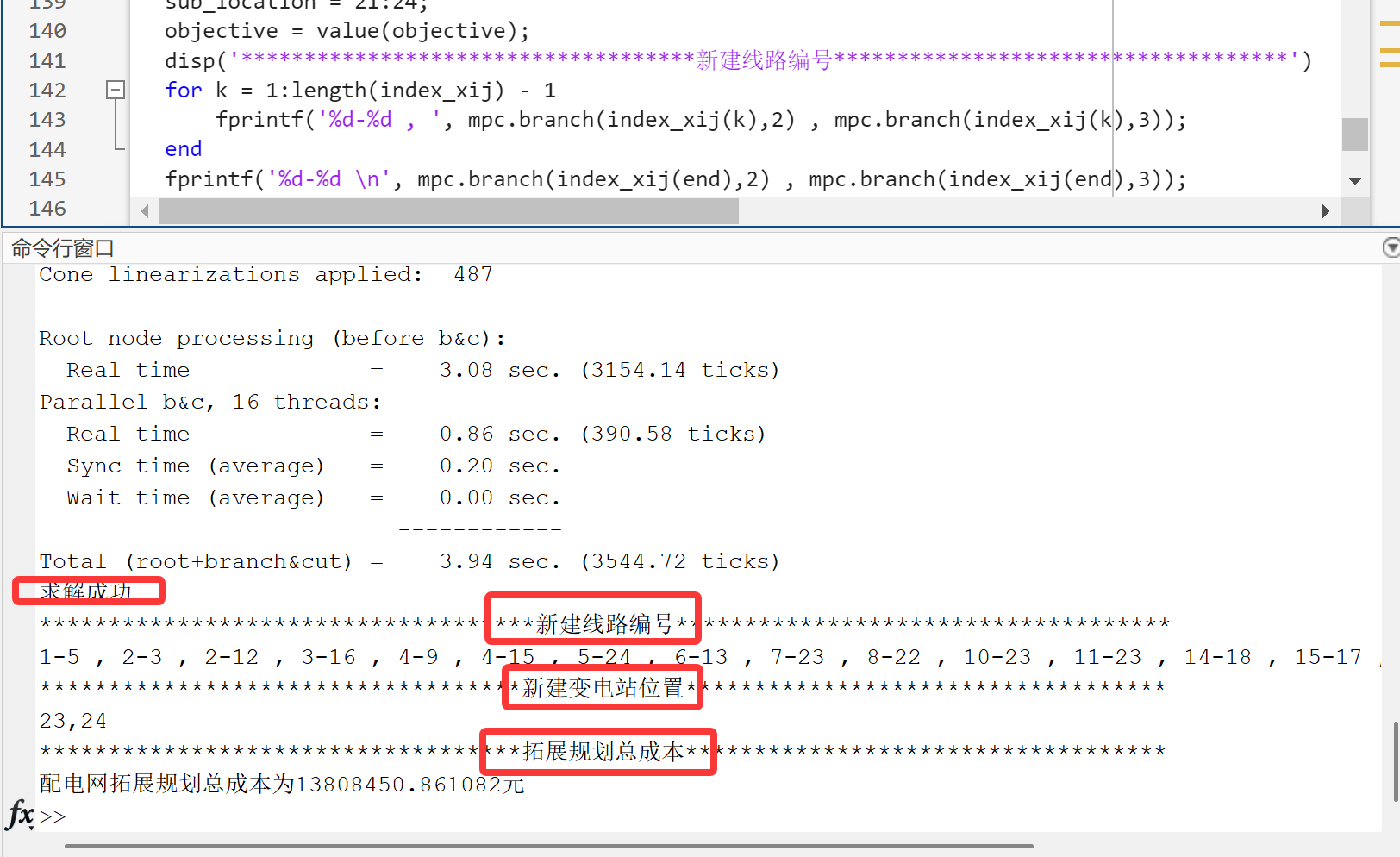
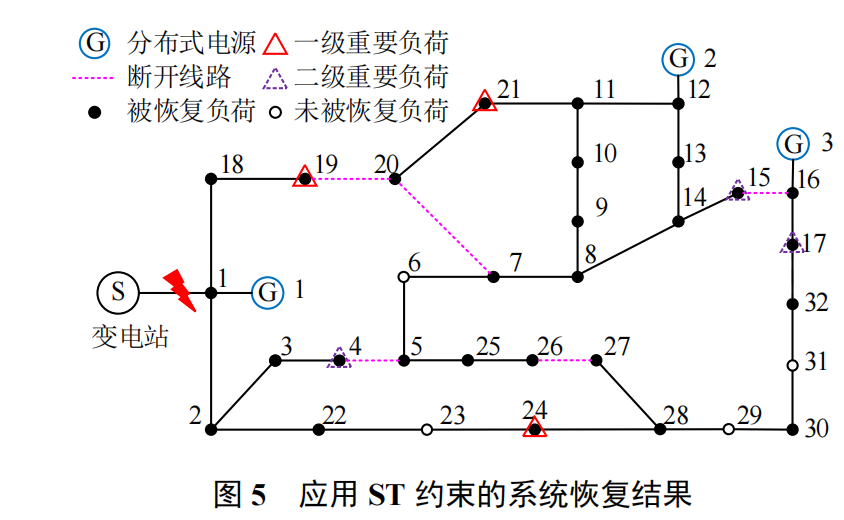
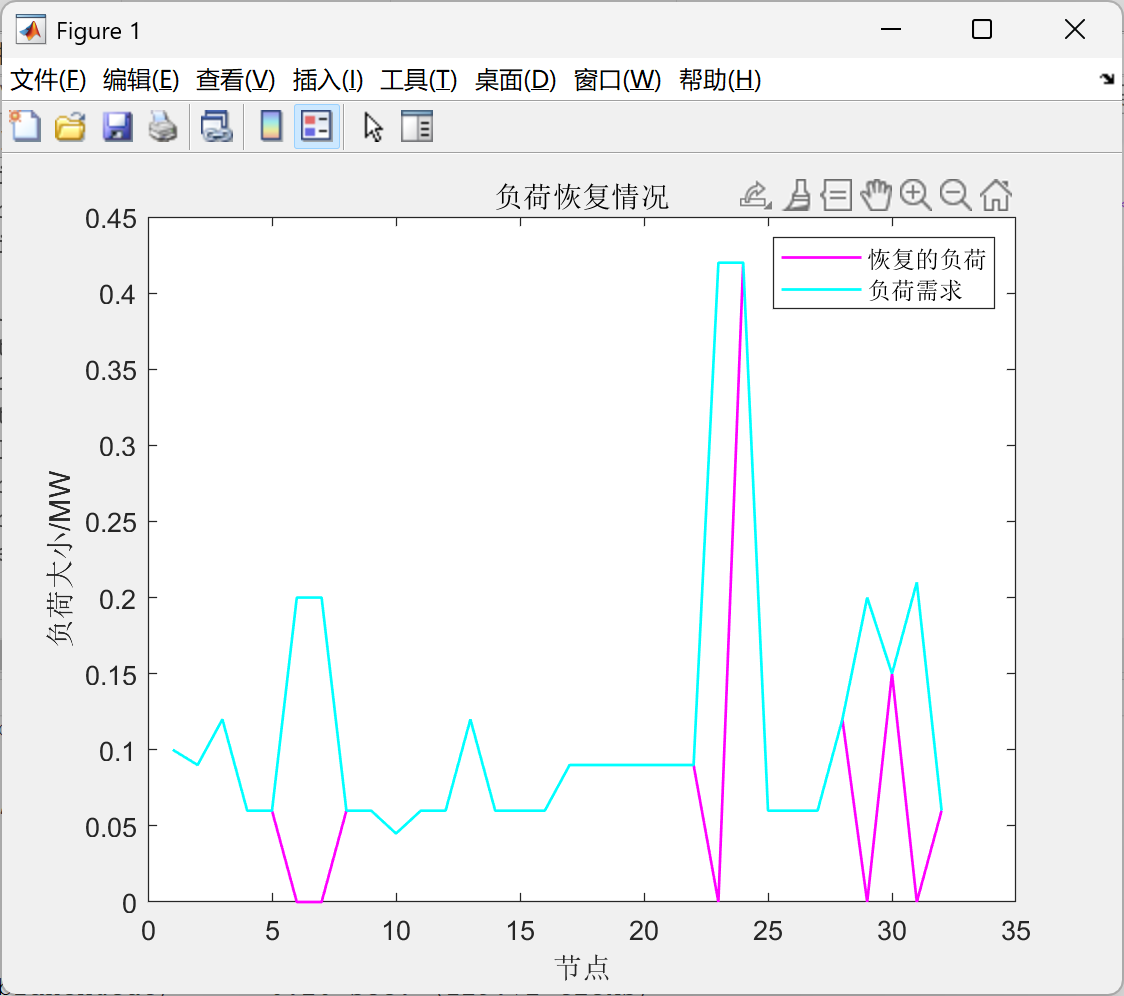
2.2 配电网故障恢复问题
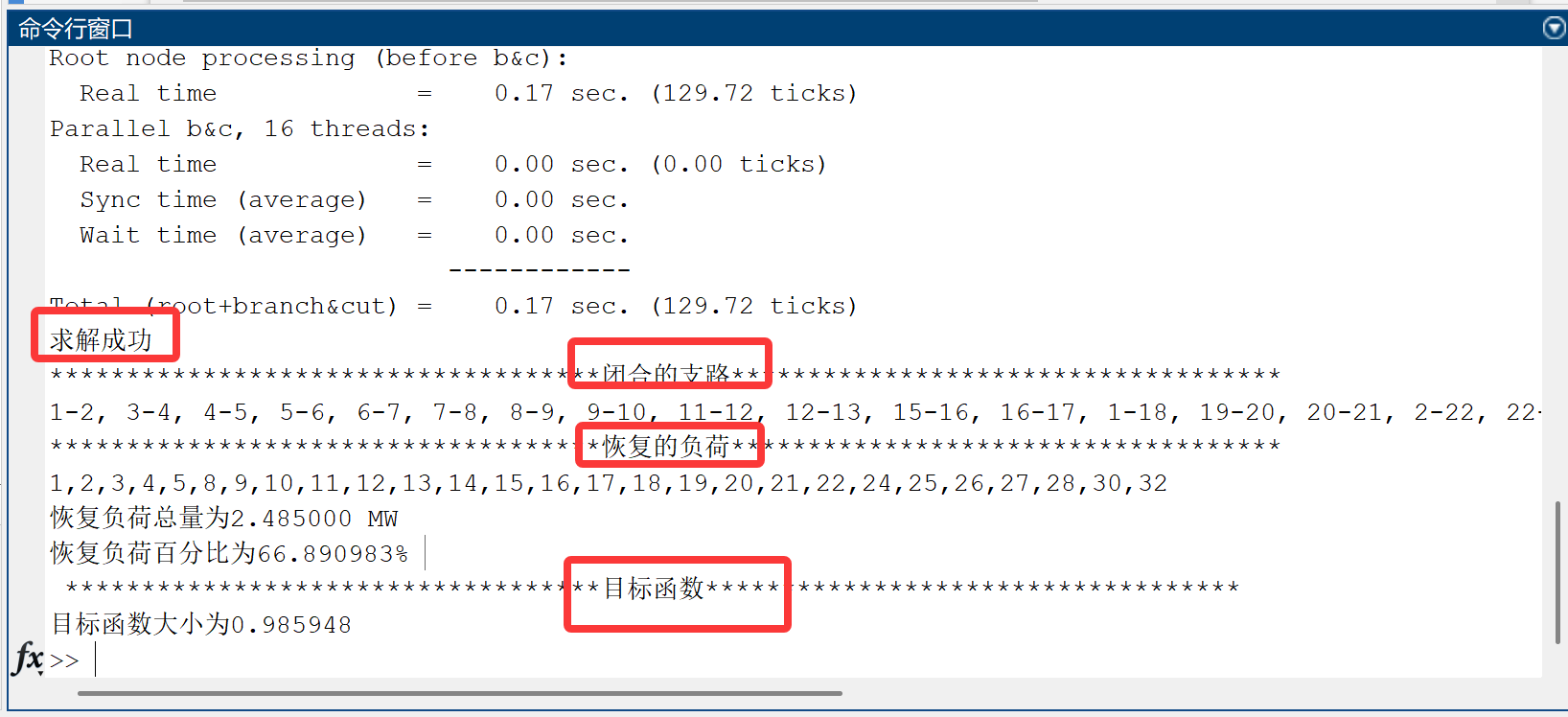
部分代码:
%% 运行结果
xij = value(xij);
zi = value(zi);
index_xij = find(xij ~= 0);
index_zi = find(zi ~= 0);
objective = value(objective);
disp('************************************闭合的支路************************************')
for k = 1:length(index_xij) - 1
fprintf('%d-%d, ', mpc.branch(index_xij(k),1) , mpc.branch(index_xij(k),2));
end
fprintf('%d-%d \n', mpc.branch(index_xij(end),1) , mpc.branch(index_xij(end),2));
disp('************************************恢复的负荷************************************')
YB = 1:32;
for k = 1:length(index_zi) - 1
fprintf('%d,', YB(index_zi(k)));
end
fprintf('%d \n', YB(index_zi(end)));
fprintf('恢复负荷总量为%f MW\n', sum(zi.*pload_i)*SB);
fprintf('恢复负荷百分比为%f%% \n', sum(zi.*pload_i)/sum(pload_i)*100);
disp(' ***********************************目标函数***********************************')
fprintf('目标函数大小为%f \n', objective);
figure
plot(zi.*pload_i*SB,'m','linewidth',1)
hold on
plot(pload_i*SB,'c','linewidth',1)
title('负荷恢复情况')
xlabel('节点')
ylabel('负荷大小/MW')
legend('恢复的负荷','负荷需求')🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]王颖,许寅,和敬涵,等.基于断线解环思想的配电网辐射状拓扑约束建模方法[J].中国电机工程学报,2021,41(07):2395-2404.
🌈4 Matlab代码、数据、说明文档、文章下载
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取






















 883
883

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








