基于粒子群优化算法的分布式电源选址与定容【多目标优化】【IEEE33节点】（Matlab代码实现）

最新推荐文章于 2025-09-16 00:01:47 发布

原创最新推荐文章于 2025-09-16 00:01:47 发布 · 266 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #分布式 #matlab #支持向量机

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

分布式电源接入配电网，实现就地消纳，可以提高新能源的利用率、提高电能质量和降低系统网损。然而接入点位置和电源的容量的差异对配电网的影响不同，如果位置和容量不合适，可能会导致系统中某处的电压越限、总系统的网损增加。因此在电源规划阶段分析分布式电源接入点的位置和容量十分有必要。分布式电源接入点和接入容量的选择问题是一个非线性、多变量、多约束的问题。目前国内外关于这方面的研究主要集中在两个方面，一是数学模型的优化，二是模型求解和算法优化。已有的诸多研究取决与分布式电源的种类，即是否只向电网提供有功功率。而且很多算法

利用准确的损耗公式，计算时需要准确阻抗矩阵和雅可比矩阵，计算效率低。因此针对不同大小、复杂性，有待于找出一种适用于所有情况的方法。本文提出了一种确定分布式电源的最佳容量和位置的分析，该方法计算效率高，适用范围广。

1.1 目标函数

(1)以系统有功网损最小和电压偏差最小建立多目标优化数学模型，其目标函数为：

式中：N为支路总数；Pi和Qi分别为第i条支路的有功与无功功率；Ui为第i条支路的末端节点电压；Ri为第i条支路的电阻；ki为第i条支路的开关状态，0代表断开，1代表闭合；f1为总有功损耗。t为节点编号；k为节点总数；Uts、UtN分别表示第t个节点的实际电压与额定电压；f2表示电压偏移量。

(2)光伏消纳量增加通常也会引起网络损耗的增加，为真实体现系统中光伏的有效消纳，在此将光伏实际消纳量与系统网络损耗的差值定义为有效消纳量Ec如下：

式中：T 为重构周期时段数；H为接入分布式光伏电源的节点数；PC(i，t )为节点i在t时段实际消纳的分布式光伏有功功率；K为配电网中的闭合支路数；Ptk、Qtk和Utk分别为支路k 在t时段的有功功率、无功功率和电压；rk为支路k的电阻。

光伏设备出力PPV如下：

其中，E 为光伏电池板数；PS(t，e )为第e个光伏电池板在t时段实际可发功率的标幺值；htmax为在t时段光照强度的最大值；Ae、ηe分别为第e个光伏电池板的面积和光电转换效率。

为了表征有效消纳量与光伏设备出力的关系，并使优化模型更为简便，将光伏设备出力和光伏有效消纳量比值定义为函数f3。则f3越小证明消纳效果越好，最小化目标函数为：

优化调度模型的目标函数F由3部分组合而成，如下式所示：

2.2 约束条件

优化的目标是得到5个接入节点和对应接入的容量，平衡节点1不接光伏，那么可接入光伏节点的取值范围为2-33；容量范围为0-2MW，步长为0.1MW

一、IEEE33节点配电系统的基本结构与特性

拓扑结构特点
IEEE33节点系统由33个节点组成，通常以节点1或节点0作为根节点（电源接入点）。系统包含多个分支结构，例如：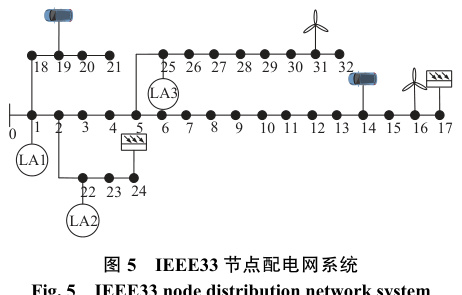
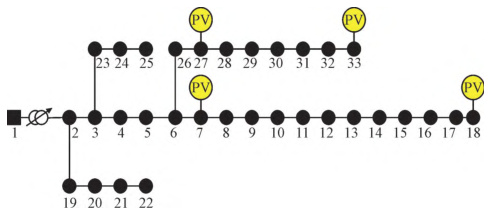
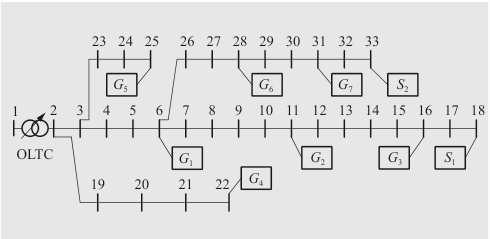
- 节点2-18-17分支；
- 节点6-26-27分支；
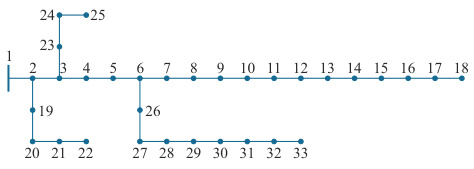
- 节点28-33分支；
- 节点19-22分支。
  网络呈现辐射状分布，线路参数以高“R/X”比为特征，导致线路损耗和电压稳定性问题显著。
负载与分布式电源配置
- 现有负载分布在节点0、18-21、25-32等位置；
- 典型DG配置包括：节点21和32的风力发电机、节点5的变压器、以及节点8、28、30附近的补偿电容器；
- 部分研究增设多组DG（如5个DG，单个容量≤300 kW）以验证优化效果。
结构对优化的影响
节点的辐射状分布和多分支特性导致潮流方向复杂，DG接入可能引发反向潮流和电压波动。例如，节点21和32的风机若容量过大，可能造成局部电压越限。

二、DG选址定容的核心挑战

多目标优化问题
DG配置需同时考虑网损最小化、电压稳定性、经济成本（如投资与运维费用）及环境效益。例如：
- 网损优化：DG可减少线路电流，但不当容量可能导致局部损耗增加；
- 电压质量：需避免电压偏差超过±5%，并通过静态电压稳定指标评估节点安全性。
混合整数非线性规划（MINLP）
DG位置（离散变量）与容量（连续变量）的联合优化导致解空间庞大，传统算法易陷入局部最优。PSO通过群体智能搜索全局最优解，但在高维问题中需结合凸松弛（如二阶锥规划）加速计算。
不确定性因素
- 风电/光伏出力波动；
- 电动汽车充电负荷的随机性；
- 负荷预测误差。
  现有研究采用多场景分析、拉丁超立方抽样等方法将不确定性转化为确定性模型。

三、粒子群优化算法的改进与应用

PSO的核心优势
- 参数简单（仅需速度、位置、惯性权重）；
- 全局搜索能力强，适合高维非凸问题；
- 易于与其他算法（如遗传算法、模拟退火）融合。
改进策略
- 参数自适应：动态调整惯性权重和加速因子，平衡探索与开发能力；
- 变异操作：在迭代中引入随机扰动，避免早熟收敛；
- 混合算法：如与模拟退火结合（SA-PSO），以概率接受次优解，增强全局搜索。
在IEEE33节点中的典型应用
- 单目标优化：以网损最小为目标，通过前推回代法计算潮流，PSO搜索最优位置与容量；
- 多目标优化：构建Pareto前沿，权衡网损、电压偏差、DG成本等目标；
- 动态场景：结合时段划分（如光伏出力高峰时段），优化DG的时序出力。

四、基于PSO的DG选址定容模型构建

模型框架
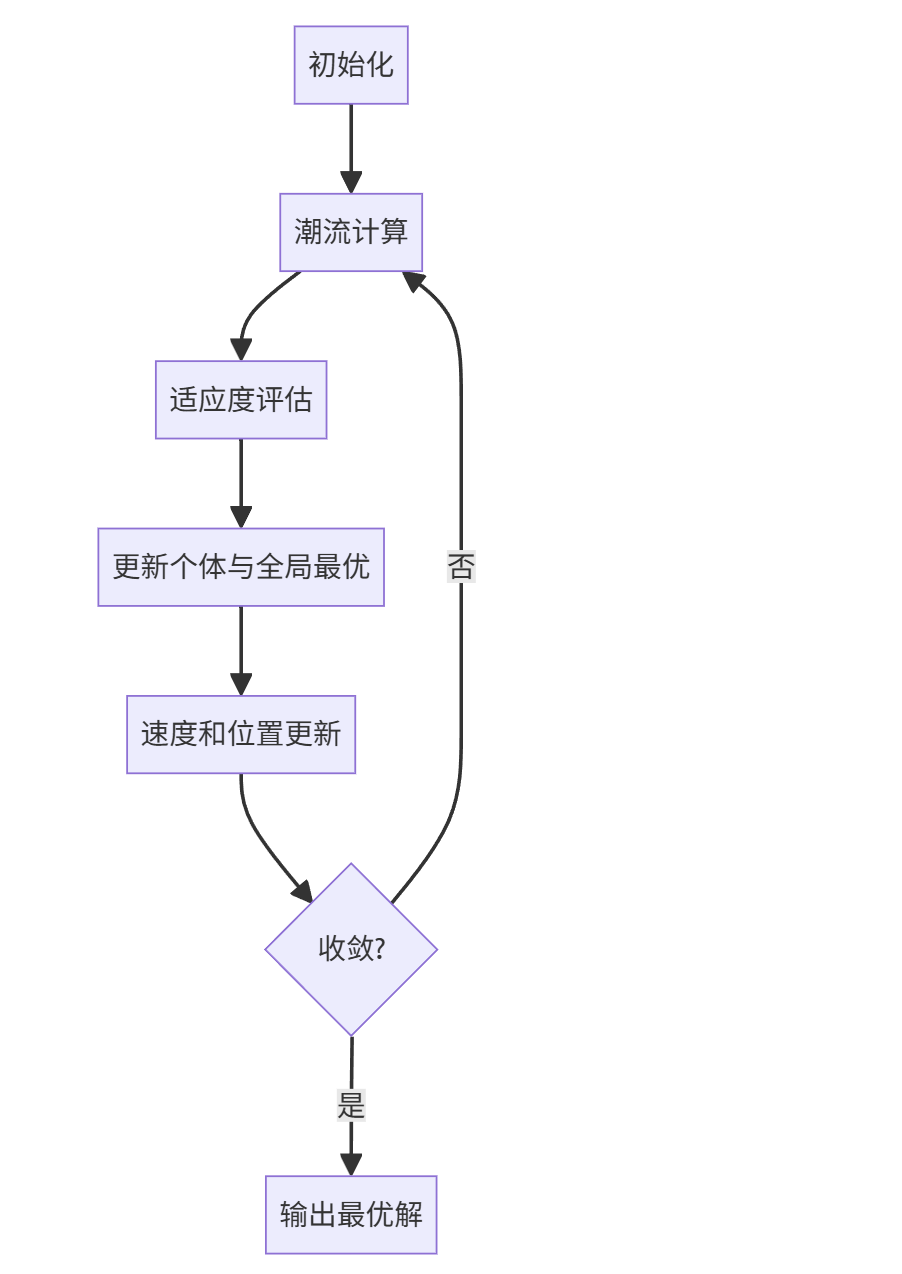
关键步骤
- 初始化：随机生成粒子群，每个粒子表示一组DG位置和容量；
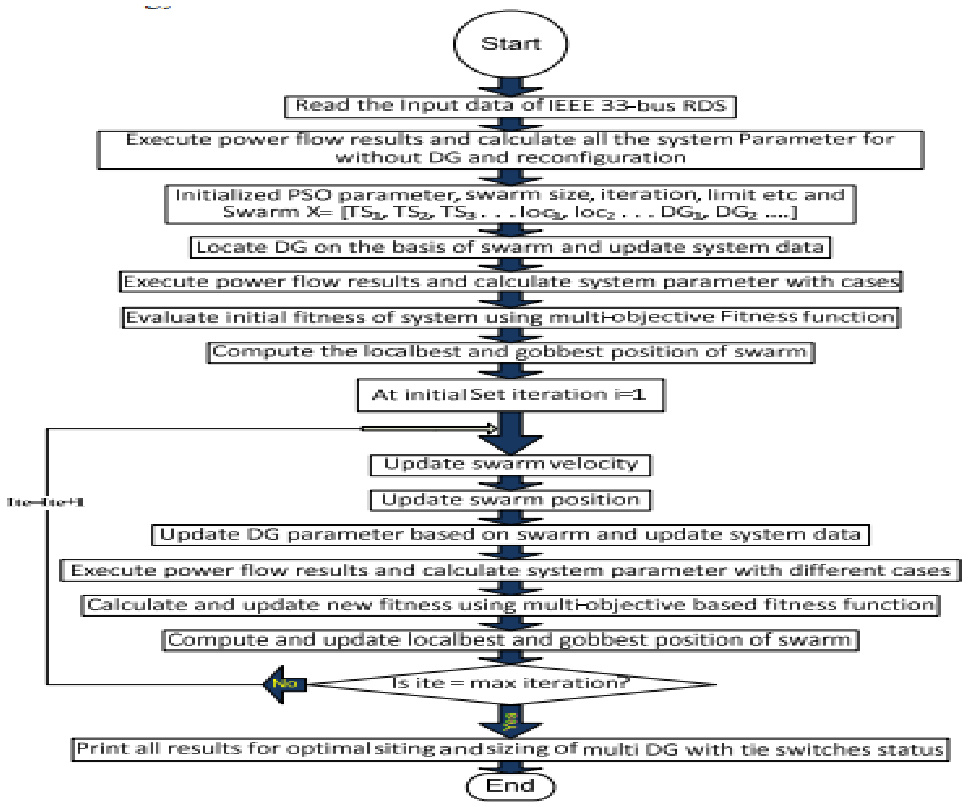
- 适应度函数：常见设计包括：

；
- 约束处理：通过罚函数法处理电压越限、容量限制等。

算例参数
- 种群规模：50-100粒子；
- 迭代次数：100-300次；
- DG容量范围：0-2 MW（依节点负荷调整）。

五、IEEE33节点系统的研究案例与结果

典型研究对比

研究案例	优化目标	算法改进	结果（网损降低）
改进海鸥算法	经济成本最小	海鸥迁移与螺旋轨迹	19.3%
多目标PSO	网损+电压偏差	自适应权重	22.5%
灰狼算法	网损+电压质量	变异操作	18.7%
混合SA-PSO	综合成本（投资+运维）	模拟退火扰动	24.1%

优化效果分析
- 电压提升：DG接入后，末端节点电压从0.90 p.u.升至0.95-0.98 p.u.；
- 经济性：最优配置下，DG投资回收期可缩短至5-8年；
- 收敛性：改进PSO的收敛速度较标准PSO提升30%以上。

六、拓扑结构对PSO收敛性的影响

节点复杂性
IEEE33节点的多分支结构导致搜索空间维度高（如5个DG时需优化10个变量），传统PSO易陷入局部最优。
改进策略
- 拓扑约束：通过破圈法限制无效拓扑生成，减少粒子无效搜索；
- 混合拓扑结构：结合星型与环形拓扑，平衡全局与局部搜索；
- 局部精细化搜索：在收敛后期缩小搜索范围，提升解精度。

七、目标函数设计要点

多目标权衡
- 权重法：为不同目标分配权重（如网损60%、电压30%、成本10%）；
- Pareto前沿：通过非支配排序保留多样化解集，供决策者选择。
不确定性建模
- 风电/光伏出力采用Beta分布或高斯混合模型；
- 电动汽车负荷通过蒙特卡洛模拟生成典型场景。
惩罚函数设计
- 电压越限惩罚系数需远高于经济目标，优先保障安全；
- 容量越限惩罚采用分段函数，避免过度约束。

结论

基于PSO的DG选址定容在IEEE33节点系统中已取得显著成效，但仍需进一步研究：

动态场景扩展：考虑实时电价与负荷波动；
高比例DG接入：探索含储能的多时间尺度优化；
算法融合：结合深度学习提升PSO的搜索效率。

以上研究为高渗透率DG的规划提供了理论支撑，未来可结合实际电网数据验证工程可行性。

📚2 运行结果

部分代码：

Ppv=sum(x(6:10))*0.1;%光伏消纳总量
f1=P1*SB;%总损耗
f2=sum(abs(U-1));%电压偏差
w1=100;w2=100;w3=1;
Ec=Ppv-f1;
f3=Ppv/Ec;
F=w1*f1+w2*f2+w3*f3+KU*SU+KI*SI;
disp('网损/kW')
f1*1000
disp('电压偏差/pu：')
f2
disp('出力消纳比为：')
f3

....

xlabel('迭代次数');
ylabel('目标函数值');
title('迭代收敛图')
hold on;
grid on;
disp('光伏接入点为:')
BestSol1.Position(1:5)
disp('对应接入容量为/MW:')
BestSol1.Position(6:10)*0.1