使用量子自适应变换进行信号和图像去噪（Matlab实现）

大龙不吃小鱼干

于 2025-07-26 08:30:50 发布

阅读量84

点赞数 3

CC 4.0 BY-SA版权

文章标签： matlab 量子计算开发语言

本文链接：https://blog.youkuaiyun.com/F_Matlab/article/details/149659422

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、量子自适应变换（QAB）概述

二、QAB在信号去噪中的应用

三、QAB在图像去噪中的应用

四、QAB算法的优势

五、未来展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

在信号和图像处理领域，去噪是一项关键任务，旨在去除信号或图像中的噪声，提高其质量和可读性。传统的去噪方法在一定程度上取得了成功，但随着技术的不断发展，新的方法不断涌现。量子计算作为一种具有巨大潜力的计算模式，为信号和图像去噪提供了新的思路和方法。其中，使用量子自适应变换进行信号和图像去噪成为了一个研究热点。量子计算基础量子计算利用量子力学的原理进行计算，具有并行性、纠缠性和叠加性等独特性质。量子比特是量子计算的基本单位，可以同时处于多个状态。通过量子门操作，可以对量子比特进行状态变换和计算。在未来，量子自适应变换有望在以下领域得到应用： 1. 通信领域：提高信号的质量和可靠性，减少噪声对通信系统的影响。 2. 医疗影像：去除医学图像中的噪声，提高诊断的准确性。 3. 图像处理：改善图像的质量，增强图像的细节和清晰度。 4. 科学研究：在天文学、物理学等领域，去除噪声对观测数据的影响，提高研究的精度。总之，使用量子自适应变换进行信号和图像去噪是一个具有挑战性和前景的研究方向。随着量子计算技术的不断发展和完善，相信这种方法将在信号和图像处理领域发挥越来越重要的作用。

使用量子自适应变换（QAB）进行信号和图像去噪研究是一个结合了量子计算思想和传统信号处理技术的创新方向。以下是对该领域研究的详细探讨：

一、量子自适应变换（QAB）概述

量子自适应变换（QAB）是一种基于量子计算思想的信号和图像处理方法，它利用量子机制中的超位置和叠加原理来优化信号处理过程。在QAB中，信号或图像被视为薛定谔方程中的势能，通过构建与信号或图像相关的量子基（QAB），实现对信号或图像的有效表示和去噪。

二、QAB在信号去噪中的应用

在信号去噪领域，QAB算法能够通过以下步骤实现信号的去噪处理：

信号分解：将原始信号分解为一系列与信号特征相关的量子基（QAB）上的系数。这些系数能够更准确地反映信号的本质特征，同时降低噪声的干扰。
噪声抑制：在量子基（QAB）域中，利用量子机制对噪声进行抑制。由于QAB能够更好地捕捉信号的结构信息，因此能够在保留信号细节的同时，有效去除噪声成分。
信号重构：将经过噪声抑制的量子基（QAB）系数重构回原始信号域，得到去噪后的信号。

三、QAB在图像去噪中的应用

在图像去噪领域，QAB算法同样展现出了强大的去噪能力。具体步骤如下：

图像转换：将图像数据从空间域转换到频率域。这一步骤通常通过傅里叶变换或小波变换等方法实现。然而，在QAB算法中，图像被转换为与图像特征相关的量子基（QAB）上的表示。
量子噪声滤波：在量子基（QAB）域中，对图像进行噪声滤波处理。通过利用量子机制中的超位置和叠加原理，QAB算法能够更有效地识别和抑制图像中的噪声成分。
图像重构：将经过噪声滤波处理的量子基（QAB）表示重构回空间域，得到去噪后的图像。这一步骤通常通过逆变换实现，如逆傅里叶变换或逆小波变换等。然而，在QAB算法中，则通过逆量子变换实现。

四、QAB算法的优势

相比传统的信号和图像去噪方法，QAB算法具有以下优势：

更高的去噪效果：由于QAB能够更准确地捕捉信号和图像的结构信息，因此能够在保留信号和图像细节的同时，更有效地去除噪声成分。
更强的适应性：QAB算法是基于信号和图像本身特征构建的量子基（QAB），因此能够根据不同的信号和图像特征进行自适应调整，实现更好的去噪效果。
更低的计算复杂度：虽然量子计算本身具有较高的计算复杂度，但QAB算法通过优化信号和图像在量子基（QAB）域中的表示和处理过程，能够在一定程度上降低计算复杂度，提高处理速度。

五、未来展望

随着量子计算技术的不断发展，QAB算法在信号和图像去噪领域的应用前景将更加广阔。未来，可以进一步探索QAB算法与其他信号处理技术的结合应用，如与深度学习、神经网络等技术的结合，以实现更高效、更智能的信号和图像去噪处理。同时，随着量子计算硬件的不断进步和成本的降低，QAB算法的实际应用也将逐步成为可能。

📚2 运行结果

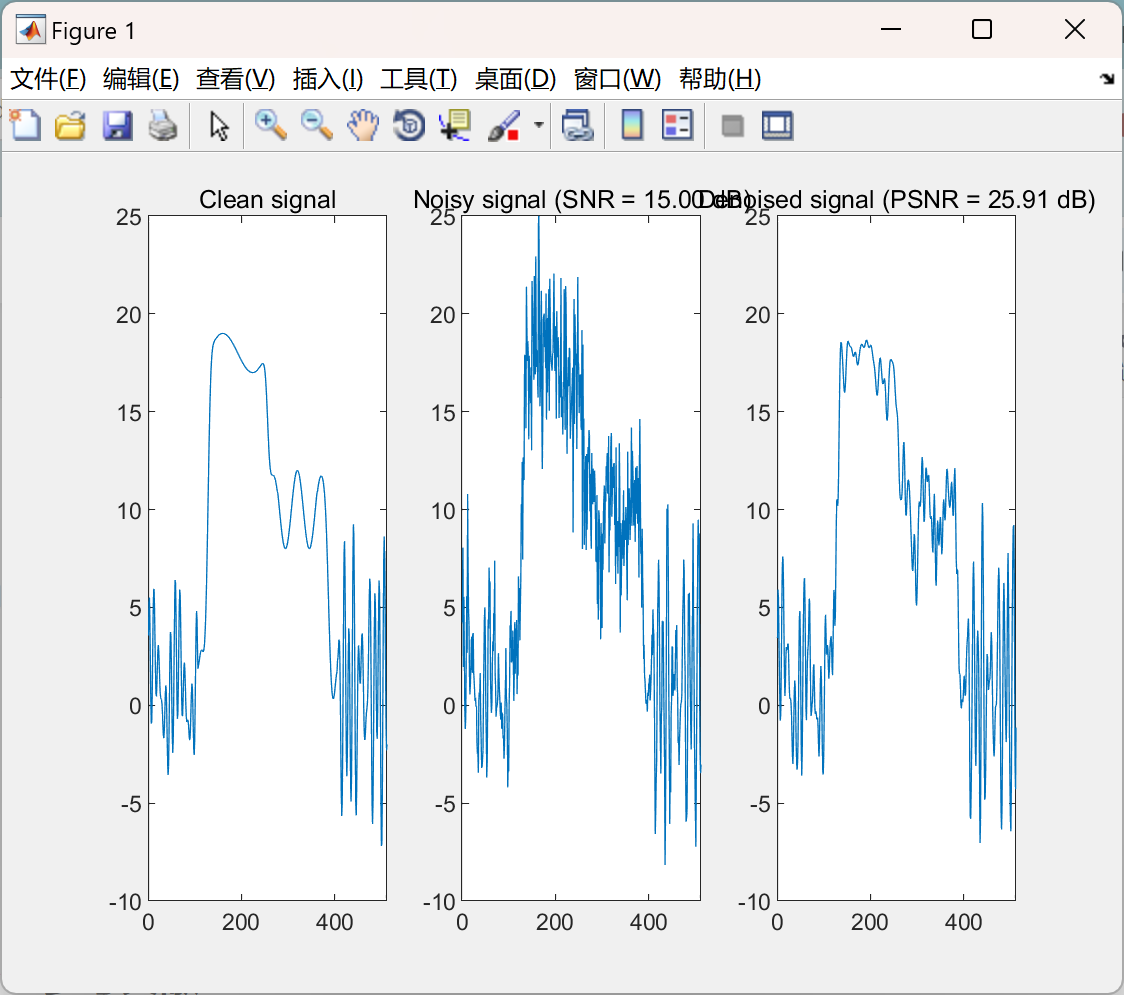
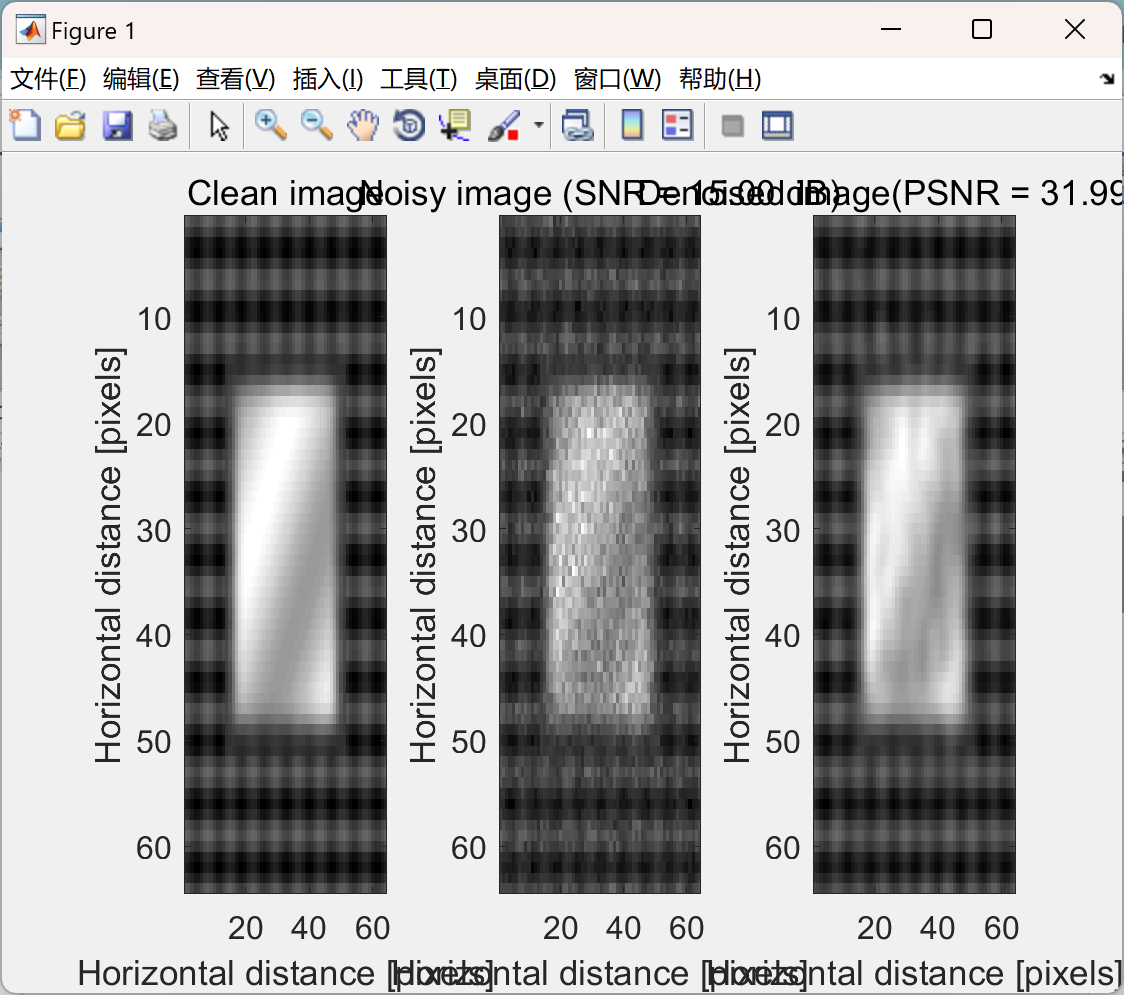
部分代码：

close all
clc; clear;

%load data
load('sample_image.mat')

%size of signal
[M,N] = size(I);
NN = N^2;
%generate the noise
SNR = 15;
pI = sum(I(:) .^2) / length(I(:));
B = randn(N,N) .* sqrt(abs(I));  % Poisson noise
pB_tmp = sum(sum(B .^2)) / NN;
B = B / sqrt(pB_tmp) * sqrt(pI * 10^(- SNR / 10));
J = B + I;  %noisy image

% Data
Ms = 20; % number of iteration in reconstruction
pds = 3; % value of palnck's constant
sg = 7.5; % Gaussian Variance (smoothing)

%image denoising using QAB
[I_result] = image_denoising_QAB(I,J,Ms,pds,sg);

% Here one may think why we need I as input, since I is the clean image.
% Actually in the program, the clean image data I is used just to find out the 
% best thresholding hyperparameter. In the code, one can see that the clean 
% image I is only used for the computation of signal-to-noise-ratio (SNR) 
% and based on this one can tune the best thresholding hyperparameter.
% So, one does not need any knowledge about the clean image I for computing
% the quantum adaptive basis (QAB) and can tune the thresholding hyperparameter
% manually up to their best possible values and modify the code accordingly.
% Therefore, one should not get confused after seeing I as an input, because I
% does not have any impact on the denoising process.


% Calculation of SNR, PSNR and SSIM
pnB = sum((I_result(:) - I(:)) .^2) / length(I(:));
SNR_end = 10 * log10(pI / pnB);
PSNR_end = calc_PSNR(I,I_result);
SSIM_end = ssim_index(I_result, I, [0.01 0.03], fspecial('gaussian', 3, 1.5), max(I(:)))
% Print data
fprintf('\n\n OUTPUT:\n SNR = %.2f, PSNR = %.2f, and SSIM = %.2f \n\n',SNR_end,PSNR_end,SSIM_end);

%plot figures
font_size = 12;
figure;
subplot(1,3,1);
imagesc(I); colormap gray
xlabel('Horizontal distance [pixels]','Fontsize',font_size)
ylabel('Horizontal distance [pixels]','Fontsize',font_size)
set(gca,'FontSize',font_size);
title(sprintf('Clean image'))

subplot(1,3,2);
imagesc(J); colormap gray
xlabel('Horizontal distance [pixels]','Fontsize',font_size)
ylabel('Horizontal distance [pixels]','Fontsize',font_size)
set(gca,'FontSize',font_size);
title(sprintf('Noisy image (SNR = %.2f dB)',SNR))