通过短时倒谱(Cepstrogram)计算进行时-倒频分析研究（Matlab代码实现）-优快云博客

本文链接：https://blog.youkuaiyun.com/F_Matlab/article/details/149659414

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

1. 短时倒谱（Cepstrogram）的定义与数学基础

1.1 核心定义

1.2 关键概念解析

2. 时-倒频分析的原理与必要性

2.1 时-倒频分析 vs. 传统时频分析

2.2 优势与适用场景

3. 短时倒谱的计算流程（算法实现）

3.1 核心步骤

3.2 关键参数设计

4. 应用案例与领域实践

4.1 语音信号处理

4.2 机械故障诊断

4.3 地震信号分析

5. 与其他时频分析方法的对比

6. 工具实现与软件支持

6.1 编程实现（Matlab示例）

6.2 工程注意事项

7. 研究挑战与前沿方向

结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

1. 短时倒谱（Cepstrogram）的定义与数学基础

1.1 核心定义

短时倒谱（Cepstrogram）是短时傅里叶变换（STFT）与倒谱分析（Cepstrum）的结合，用于分析信号在时间-倒频域的联合特征。其定义为：

倒谱（Cepstrum）：信号功率谱对数的傅里叶逆变换（IDFT），数学表达式为：

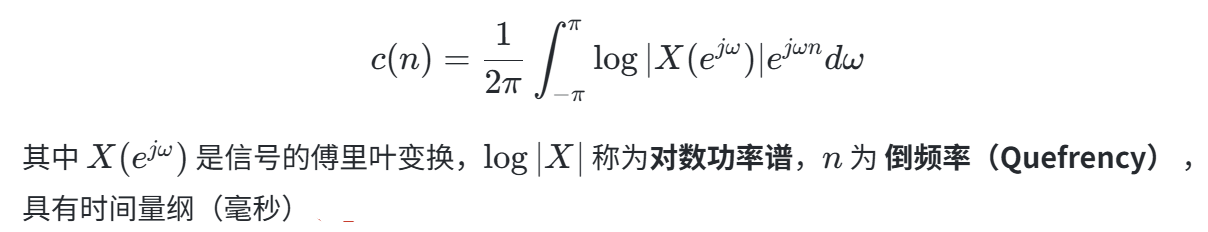
短时倒谱：通过对信号分帧加窗，计算每帧的倒谱，形成时间相关的倒谱序列：

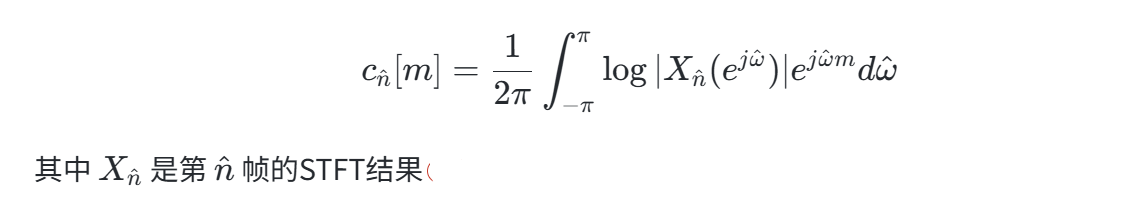
Cepstrogram：将短时倒谱的幅度按时间 n^n^ 和倒频率 mm 绘制的二维图像，直观展示信号时-倒频特征。

1.2 关键概念解析

倒频率（Quefrency）：
倒谱的横坐标，单位为时间（ms），反映信号中的周期性结构。高倒频率对应频谱快速波动（如高频噪声），低倒频率对应缓慢波动（如基频和谐波）。
复倒谱（Complex Cepstrum）：
保留对数功率谱的复数相位信息，但处理复杂（相位可能超出 (−π,π)(−π,π) 范围），实际中多使用实倒谱。
物理意义：
倒谱分离信号中的激励源（如声带振动、机械冲击）和传递系统（如声道、机械结构）。例如语音信号中，低倒频区反映声道特性，高倒频区反映基音周期。

2. 时-倒频分析的原理与必要性

2.1 时-倒频分析 vs. 传统时频分析

传统时频分析（如STFT、小波变换）：
在时间-频率域表示信号，适用于非平稳信号（如语音、振动信号），但无法分离卷积混合的源与系统。
时-倒频分析：
通过倒谱将频域周期性转化为倒频域脉冲，直接分离激励与系统响应。例如：
- 语音中分离声道（低倒频）和声带振动（高倒频）；
- 故障诊断中提取轴承损伤的周期性冲击。

2.2 优势与适用场景

场景	问题	时-倒频分析的解决方案
语音处理	共振峰靠拢导致分辨率不足	倒谱分离声道与激励，精确提取共振峰
机械故障诊断	背景噪声掩盖周期性冲击	对数变换增强弱冲击，倒频域凸显周期
地震信号分析	地层反射波与噪声耦合	倒谱剔除多次反射，保留有效波

3. 短时倒谱的计算流程（算法实现）

3.1 核心步骤

信号分帧与加窗：
- 输入信号 x(t) 分成长度为 N 的帧，帧移 H（跳跃长度）。
- 加窗（如Hamming窗）减少频谱泄露：
```
win = hamming(wlen, 'periodic');  % 
```

3.2 关键参数设计

窗长选择：
长窗提高频率分辨率（适合稳态信号），短窗提高时间分辨率（适合瞬变信号）。
倒频域截断：
低倒频区（<1ms）保留系统响应，高倒频区（>5ms）提取周期性冲击。

4. 应用案例与领域实践

4.1 语音信号处理

基音检测：
倒谱峰值对应基音周期（如男性基音约5ms，女性约3ms）。
声道估计：
低倒频系数重建声道传递函数，用于语音合成与识别。

4.2 机械故障诊断

轴承故障检测：
损伤点周期性冲击在倒频域表现为峰值（如轴承故障周期10ms），强于传统频谱。
齿轮箱故障：
倒谱分离齿轮啮合频率与调制边带，定位磨损齿轮。

4.3 地震信号分析

地层结构成像：
倒谱剔除地震波多次反射，保留一次反射波，提高地层分辨率。

5. 与其他时频分析方法的对比

方法	优势	局限性	与Cepstrogram的关联
STFT	计算简单，实时性强	海森堡测不准原理限制时频分辨率	Cepstrogram的基础步骤
小波变换	多尺度分析，适合瞬态信号	基函数选择依赖经验	可替代STFT作为倒谱输入
Wigner-Ville	高时频分辨率	交叉项干扰多分量信号分析	需配合倒谱抑制交叉项
Cepstrogram	分离激励与系统，增强周期性	对噪声敏感，需预滤波	—

典型组合应用：

STFT + 倒谱：滚动轴承故障诊断中，先用STFT得时频谱，再对每帧功率谱作倒谱分析提取冲击周期。
小波变换 + 倒谱：肌电信号分析中，小波分解后对子带信号计算倒谱，提高特征可分性。

6. 工具实现与软件支持

6.1 编程实现（Matlab示例）

% 输入信号x，采样率fs
[C, q, t] = cepstrogram(x, win, hop, fs);  % 核心函数[[18]]

% 可视化
imagesc(t, q, abs(C));
xlabel('Time (s)'); ylabel('Quefrency (ms)');

工具包推荐：
- MATLAB时频工具箱（tftb）：支持STFT、Cepstrogram。
- Python库librosa：提供cepstrogram接口。

6.2 工程注意事项

噪声抑制：对数变换放大低频噪声，需预滤波或加权处理。
实时性优化：FFT加速IDFT计算，窗长按信号特性自适应调整。

7. 研究挑战与前沿方向

交叉项干扰：
多分量信号在倒频域产生虚假峰值，需设计核函数抑制（如自适应核时频分布）。
非线性信号处理：
希尔伯特-黄变换（HHT）与倒谱结合，处理非平稳信号。
深度学习融合：
用CNN从Cepstrogram中自动学习特征，提升故障分类精度（如轴承故障诊断）。

结论

短时倒谱（Cepstrogram）通过将时频分析（STFT）与倒谱变换结合，在倒频域实现了激励源与传递系统的分离，显著提升了周期性特征的提取能力。其在语音处理、机械故障诊断、地震信号分析等领域的成功应用，验证了其解决复杂非平稳信号问题的有效性。未来研究需进一步优化抗噪性、实时性及非线性适应能力，并结合深度学习挖掘高维特征潜力。

📚2 运行结果

部分代码：

% load a sound file
[x, fs] = audioread('sample2.wav'); % load an audio file
x = x(:, 1); % get the first channel
x = x/max(abs(x)); % normalize the signal
N = length(x); % signal length
t1 = (0:N-1)/fs; % time vector

% define the analysis parameters
wlen = 1024; % window length (recomended to be power of 2)
hop = 256; % hop size (recomended to be power of 2)

% calculate the cepstrogram
win = hamming(wlen, 'periodic');
[C, q, t2] = cepstrogram(x, win, hop, fs);

% some conditioning
C = C(q > 0.5e-3, :); % ignore all cepstrum coefficients for
% quefrencies bellow 0.5 ms
q = q(q > 0.5e-3); % ignore all quefrencies bellow 0.5 ms
q = q*1000; % convert the quefrency to ms