👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
直流潮流发的特点是用电力系统的交流潮流(有功功率和无功功率)用等值的直流电流来代替。甚至只用直流电路的解析法来分析电力系统的有功潮流,而根不如你不考虑无功分布对有功的影响。这样一来计算速度加快,但计算的准确度有所降低,本方法适用于对潮流计算准确度要求不高的计算场景。
下面先对直流潮流法的原理进行简单介绍:

上图为直流法的等值图,在上图所示的输电线路中,有功潮流为:

为了快速计算的需要,将上式进行了三项简化:
(1)考虑一般高压电网中线路的电阻远小于电抗,对地电导也可以忽略即 Gii=0 Gij =0
(2)按照标幺值计算时,节点电压与其额定电压相差不大,故有:Ui≈Uj≈1.0;
(3)线路两端的电压相角差(θi-θj)较小,所以有:

这样,上式前两项均为零,只剩第三项

这就相当于线路两端的直流电位分别为θi和θj。线路的直流电阻是Xij。则用矩阵表示为如下式所示。

式中:B0为正常运行时网络的节点电纳矩阵;
θ为网络中各节点的电压相位角的向量;
P为节点注入的有功功率向量;
一、直流潮流计算基本原理
1. 核心思想与简化假设
直流潮流法通过线性化近似简化交流潮流方程,仅分析有功功率分布,忽略无功潮流和电压幅值变化。其简化基于三个关键假设:
- 假设1:高压电网中线路电阻远小于电抗(r≪xr≪x),忽略电阻和对地电导。
- 假设2:节点电压标幺值近似为1.0 p.u.(与额定电压偏差小)。
- 假设3:线路两端电压相角差极小(sinθij≈θijsinθij≈θij)。
2. 数学模型
-
节点功率方程:
P=B′θ
其中:
- P为节点注入有功功率向量(除参考节点外),
- θ为节点电压相角向量,
- B′为简化节点电纳矩阵(维度n×nn×n,nn为节点数)。
-
支路潮流方程:
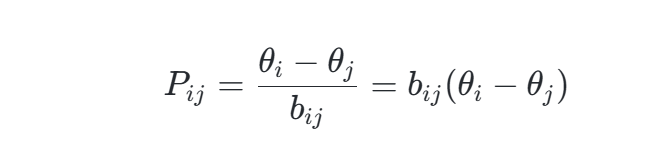
bij为支路i−j的电纳(导纳虚部)。
-
B′B′矩阵构建步骤:
- 从交流节点导纳矩阵YY中提取虚部(忽略电阻)。
- 对角元素替换为所有连接支路电纳之和。
- 非对角元素为支路电纳的负值。
- 移除参考节点(通常为平衡节点)对应的行和列。
3. 算法特点
- 优势:计算速度快、无收敛性问题(线性方程)、适用于大规模网络预想事故分析。
- 局限性:忽略有功损耗和无功分布,误差约3%-10%,不适用于精确调度。
二、IEEE 9节点系统拓扑与参数
1. 基础拓扑结构
-
节点类型:
节点 类型 设备 1 平衡节点 水电机组G1 2 PV节点 火电机组G2 3 PQ节点 新能源场站 4-9 PQ节点 负荷 -
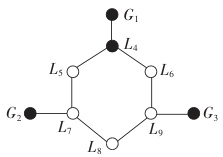
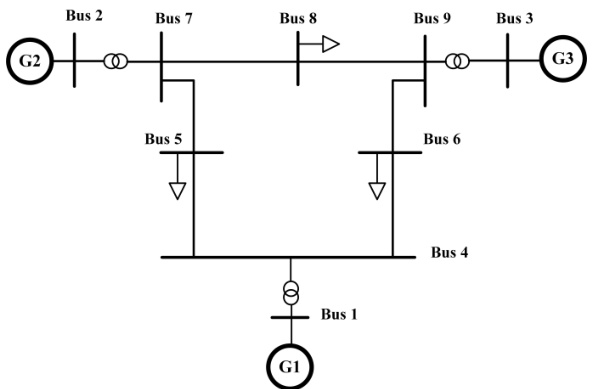
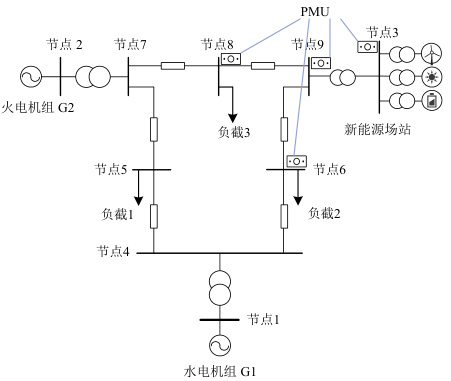
关键连接(见图1):
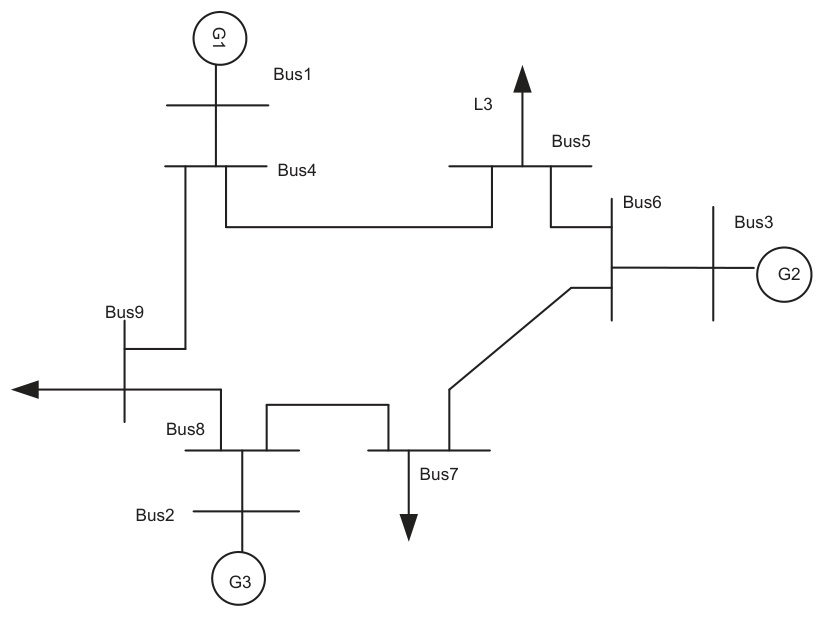
- 发电机:G1→节点1, G2→节点2, G3→节点3(改进版含风电)。
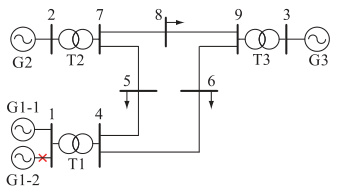
- 变压器:T1(节点1-4)、T2(节点2-7)、T3(节点3-9)。
- 线路:L1(4-5)、L2(5-6)、L3(7-8)等共9条支路。
- 发电机:G1→节点1, G2→节点2, G3→节点3(改进版含风电)。
2. 典型参数(标幺值)
| 支路 | 首端节点 | 末端节点 | 电阻 rr | 电抗 xx |
|---|---|---|---|---|
| L1 | 4 | 5 | 0.0001 | 0.0125 |
| L2 | 5 | 6 | 0.0003 | 0.0250 |
| T1 | 1 | 4 | 0.0015 | 0.0576 |
| 节点 | 类型 | 注入有功 (MW) | 电压 (p.u.) |
|---|---|---|---|
| 1 (G1) | Slack | - | 1.0 |
| 2 (G2) | PV | 150 | 1.0 |
| 3 (风电) | PQ | 90 | - |
注:新能源改进版在节点3接入风电场,切入风速3m/s,额定风速13m/s。
三、直流潮流计算实现步骤(以IEEE 9节点为例)
1. 算法流程
-
选择平衡节点(通常为节点1)。
-
构建B′B′矩阵:
- 基于支路电抗xij计算电纳bij=1/xij。
- 按节点拓扑填充B′(对角元素为相连支路电纳之和,非对角元素为−bij−bij)。
-
形成注入功率向量PP:

-
求解相角向量:
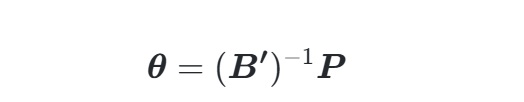
-
计算支路潮流:
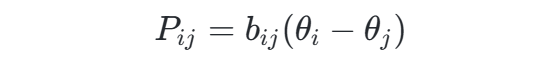
2. MATLAB程序核心代码
function [branch_power, node_angle] = dc_power_flow(bus, branch)
% 构建B'矩阵
n = max(bus(:,1)); % 节点数
B_prime = zeros(n-1, n-1); % 排除平衡节点
for k = 1:size(branch,1)
i = branch(k,1); j = branch(k,2);
if i > 1 && j > 1
B_prime(i-1,j-1) = B_prime(i-1,j-1) - 1/branch(k,4); % branch(k,4)=x
B_prime(j-1,i-1) = B_prime(j-1,i-1) - 1/branch(k,4);
end
if i > 1, B_prime(i-1,i-1) = B_prime(i-1,i-1) + 1/branch(k,4); end
if j > 1, B_prime(j-1,j-1) = B_prime(j-1,j-1) + 1/branch(k,4); end
end
% 注入功率向量(除平衡节点)
P = [bus(2:end, 3)]; % 第3列为有功注入
% 求解相角
theta = B_prime \ P; % 线性方程组求解
node_angle = [0; theta]; % 平衡节点相角=0
% 计算支路潮流
branch_power = zeros(size(branch,1),1);
for k = 1:size(branch,1)
i = branch(k,1); j = branch(k,2);
branch_power(k) = (1/branch(k,4)) * (node_angle(i) - node_angle(j));
end
end
3. 计算结果输出示例
| 节点 | 电压相角 (rad) | 支路 | 有功潮流 (MW) |
|---|---|---|---|
| 1 | 0 | L1 (4-5) | 45.2 |
| 2 | -0.012 | T1 (1-4) | 72.1 |
| 3 | -0.025 | L3 (7-8) | -28.3 |
四、新能源接入对直流潮流的影响分析
1. 风电波动性建模
-
风电场接入节点3,功率输出Pw随风速v变化:

2. 对潮流分布的影响
- 场景1(额定风速) :节点3注入90MW,导致相邻支路(如L2:5-6)潮流增加12%。
- 场景2(风速波动) :风速从8m/s升至13m/s时,节点3相角变化Δθ3=−0.01radΔθ3=−0.01rad,引发支路L5(6-4)过载风险。
3. 改进直流潮流法的应用
-
网损修正模型:在传统直流方程中加入近似网损项,提升精度至误差<5%:
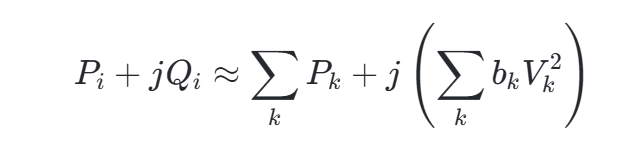
-
线性锥规划(SOCP) :处理含风电最优潮流问题,兼顾速度与精度(见表1):
方法 计算时间 (s) 最大误差 (%) 传统直流潮流 0.02 9.8 SOCP 0.35 2.1
五、工程应用与扩展建议
- 预想事故分析:基于直流灵敏度法快速筛选关键故障支路(如∂Pij/∂xk>ϵ∂Pij/∂xk>ϵ)。
- 经济调度优化:结合低碳约束,以min∑(cgPg+ccarbon)min∑(cgPg+ccarbon)为目标函数,嵌入直流潮流约束。
- 工具推荐:
- Matlab:自定义脚本灵活度高。
- Pandapower:支持IEEE 9节点BPA参数导入与可视化。
- CloudPSS/SimStudio:内置标准模板,一键生成潮流报告。
注:完整参数表及代码见(IEEE资源库)、(BPA数据)、(MATLAB程序)。
结论:直流潮流法在IEEE 9节点系统中可快速评估有功分布,尤其适用于含新能源的电网预规划与安全筛查,但需通过改进模型或高阶工具(如SOCP)提升精度。
📚2 运行结果
2.1 IEEE9节点
clc
close all
clear
%% 算例
mpc = case9;
%% 潮流计算
[theta1,P_branch,M,Z,slackbus] = DCpowerflow(mpc);
%% 输出结果
disp('=============================');
disp('支路潮流矩阵')
disp('=============================');
disp('')
disp([num2str(P_branch)]);
disp('=============================');
disp('节点相位矩阵')
disp('=============================');
disp('')
disp([num2str(theta1)]);clc
close all
clear
%% 算例
mpc = case9;%% 潮流计算
[theta1,P_branch,M,Z,slackbus] = DCpowerflow(mpc);%% 输出结果
disp('=============================');
disp('支路潮流矩阵')
disp('=============================');
disp('')
disp([num2str(P_branch)]);disp('=============================');
disp('节点相位矩阵')
disp('=============================');
disp('')
disp([num2str(theta1)]);

🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]连宏汇,潘欢.直流潮流计算下的孤岛处理模型[J].电工电气,2018(12):8-11+16.
[2]雷婧婷,安婷,杜正春,袁峥.含直流配电网的交直流潮流计算[J].中国电机工程学报,2016,36(04):911-918.DOI:10.13334/j.0258-8013.pcsee.2016.04.003.




















 161
161

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








