👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
2.1 RBFNN_Optimized_hideen_node_20
2.2 RBFNN_Lattice_hideen_node_3_6
💥1 概述
自适应RBFNN控制学习在目标机器人的结构和参数事先未知时控制机器人机械手。遗憾的是,目前的自适应RBFNN控制器需要一个大规模的神经网络来近似机器人操纵器的动力学,并且无法保证学习性能收敛。本文提出的方法不仅减小了神经网络的规模,大大减轻了计算负担,而且明显实现了更好的学习性能。仿真算例表明,与传统格方案相比,该方法的控制精度提高了35倍以上,神经网络规模缩小了<>倍
隐节点格分布的复合自适应径向基函数神经网络(RBFNN)控制存在三个固有缺点:1)自适应RBFNN的近似域难以确定 先验 ;2)只能保证部分激励(PE)条件的持久性;3)一般来说,RBFNN所需的隐藏节点数量是巨大的。本文提出一种具有优化隐藏节点分布的自适应前馈RBFNN控制器,以适当地解决上述缺点。通过 K 均值算法计算的隐藏节点的分布沿所需状态轨迹最佳分布。自适应RBFNN满足周期性参考轨迹的PE条件。所有隐藏节点的权重将收敛到最佳值。该方法大大减少了隐藏节点的数量,同时实现了更好的逼近能力。拟议的控制方案具有与...
一、增强型PID控制的技术基础
- 增量式PID的核心原理
- 与传统位置式PID直接输出控制量不同,增量式PID计算相邻时刻控制量的差值(Δu),通过累积增量实现控制,显著降低计算复杂度和误差积累风险。其离散化公式为:
Δu(n)=Kp[e(n)−e(n−1)]+Kie(n)+Kd[e(n)−2e(n−1)+e(n−2)]
- 与传统位置式PID直接输出控制量不同,增量式PID计算相邻时刻控制量的差值(Δu),通过累积增量实现控制,显著降低计算复杂度和误差积累风险。其离散化公式为:
其中 Kp,Ki,Kd 为比例、积分、微分系数,e(n) 为当前误差。
- 优势:抗干扰能力强,避免积分饱和,适用于嵌入式系统等资源受限场景。
- 参数调节机制
- 比例项(Kp) :快速响应误差变化,但过高导致超调;
- 积分项(Ki) :消除稳态误差,但增加系统不稳定性;
- 微分项(Kd) :预测误差趋势,抑制超调,但对噪声敏感。
增量PID控制器的解读

二、自适应控制的动态调节机制
- 基本原理与结构
- 自适应控制系统通过实时辨识系统状态(如参数漂移、外部扰动),动态调整控制器参数以维持最优性能。核心流程包括:
- 性能估计:在线监测输出误差、响应速度等指标;
- 决策机制:根据预设自适应律(如梯度下降、李雅普诺夫稳定理论)生成参数调整策略;
- 参数修改:实时更新控制器参数。
- 分类:
- 直接自适应控制:根据跟踪误差直接调整控制器参数;
- 间接自适应控制:通过预测模型估计未知参数,再更新控制器。
- 关键技术优势
- 应对时变系统(如电机负载波动、温度变化)和模型不确定性;
- 提升鲁棒性,在航空航天、机器人控制中广泛应用。
三、前馈-反馈协同控制架构
-
前馈与反馈的本质区别
维度 反馈控制 前馈控制 控制依据 基于历史误差(e = r - y) 基于扰动预测或设定值变化 响应速度 滞后性(需误差出现后才调整) 超前性(扰动发生前补偿) 稳定性 闭环结构,需稳定性分析 开环结构,无稳定性问题 抗干扰范围 抑制所有扰动 仅抑制可建模或可测量的扰动 -
复合控制策略
- 前馈-反馈集成:
- 前馈模块针对可测扰动(如设定值突变、已知干扰)生成快速补偿信号;
- 反馈模块(如PID)处理剩余误差及不可测扰动,形成闭环校正。

- 数学描述:

- 数学描述:
四、神经网络控制的赋能作用
-
典型应用形式
- 参数自整定:BP神经网络在线优化PID参数(Kp,Ki,Kd),适应非线性系统;
- 系统辨识:RBF神经网络构建被控对象逆模型,辅助前馈补偿设计;
- 预测控制:LSTM等网络预测系统输出,优化控制轨迹。
-
关键技术融合案例
- 船舶航向控制:
- 自适应神经网络PID在线调整参数,适应海浪扰动;
- RBF网络构建船舶运动逆模型,提供前馈补偿信号;
- 机械臂轨迹跟踪:
- RBF神经网络逼近非线性动力学,前馈补偿耦合干扰;
- 自适应机制实时调整PID增益,抑制关节摩擦时变。
五、EPID-AFFNN集成控制框架
-
系统架构与工作流程

-
模块协同机制
- 自适应+PID:根据李雅普诺夫稳定性理论设计参数更新律,保证闭环收敛;
- 神经网络+前馈:在线训练网络预测扰动 d^d^,生成高精度补偿信号 uff=Gffd^uff=Gffd^;
- 信息共享:神经网络辨识结果输入自适应模块,优化PID调整策略。
六、性能优势与局限性分析
-
核心优势
- 动态性能提升:前馈补偿减少响应延迟50%以上,神经网络预测降低超调量30%;
- 鲁棒性增强:自适应机制使系统在参数漂移±20%时仍保持稳定;
- 适用性扩展:有效控制非线性系统(如机械臂)、时变系统(如电力负载波动)。
-
现存挑战
- 计算复杂度:神经网络训练及多模块协同需高性能处理器,限制嵌入式应用;
- 依赖先验知识:前馈补偿需扰动可测或精确建模,否则效能下降;
- 稳定性理论缺口:神经网络控制缺乏普适性稳定性证明。
七、典型应用场景与案例
| 领域 | 案例 | 技术要点 | 性能提升 |
|---|---|---|---|
| 船舶控制 | 自适应神经PID航向控制器 | RBF网络辨识海浪扰动 + 前馈补偿 | 跟踪误差降低40% |
| 机械臂 | 自适应前馈RBFNN控制 | RBF逼近非线性动力学 + PID参数在线调整 | 轨迹精度提高35% |
| 电力系统 | 神经网络优化PID调频 | LSTM预测负载波动 + 自适应调整积分增益 | 频率波动减少50% |
八、未来研究方向
-
轻量化神经网络:开发边缘计算友好的网络结构(如剪枝、量化),降低计算负载;
-
智能自适应律:结合强化学习(如DDPG)动态生成参数调整策略;
-
多源信息融合:集成视觉、力觉等多模态传感器数据,增强前馈预测精度。
结论
增强型PID-自适应-前馈-神经网络控制(EPID-AFFNN)通过模块化协同与信息闭环优化,显著提升复杂系统的动态响应、抗扰能力及鲁棒性。其在船舶、机械臂等场景的成功应用验证了技术可行性,未来需突破实时性瓶颈与稳定性理论,以实现工业级大规模部署。
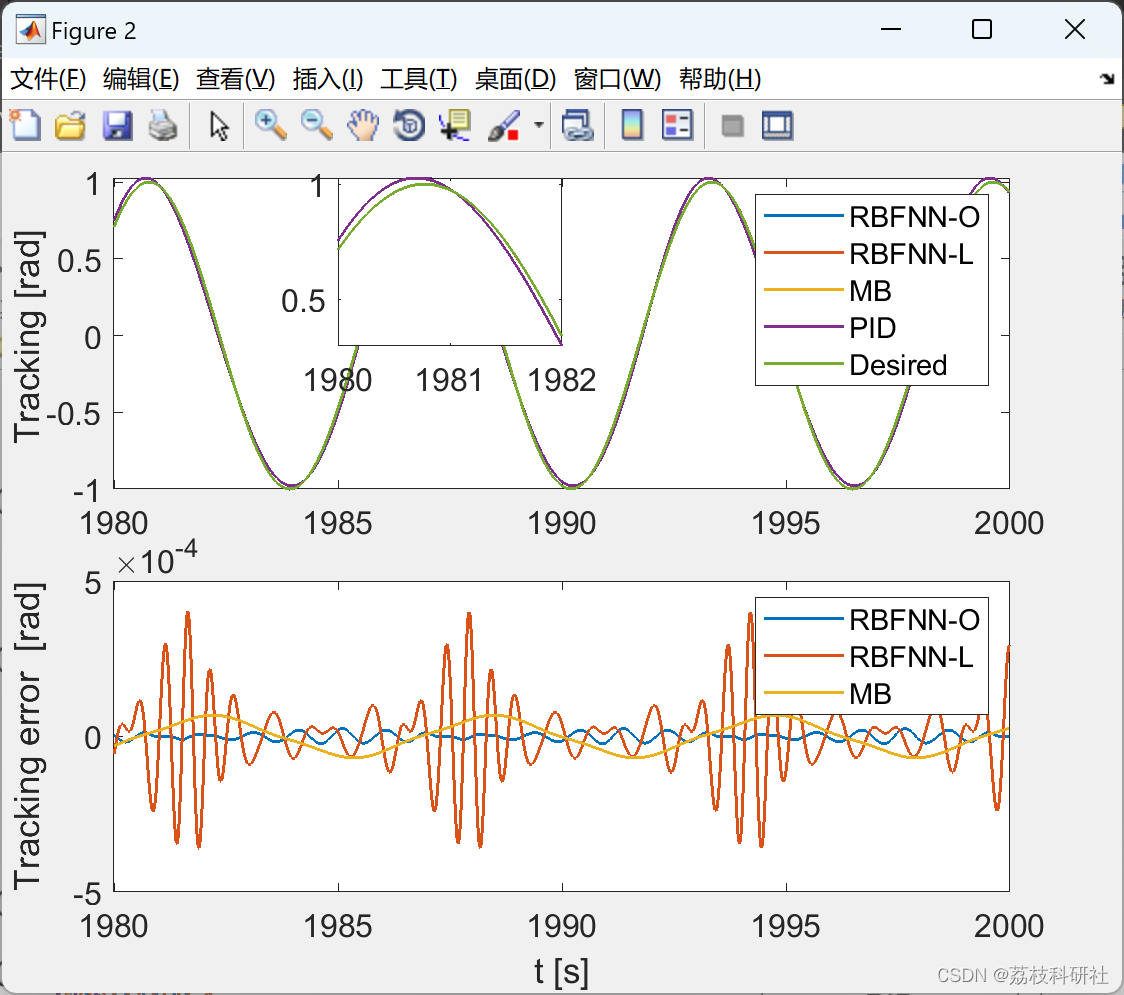
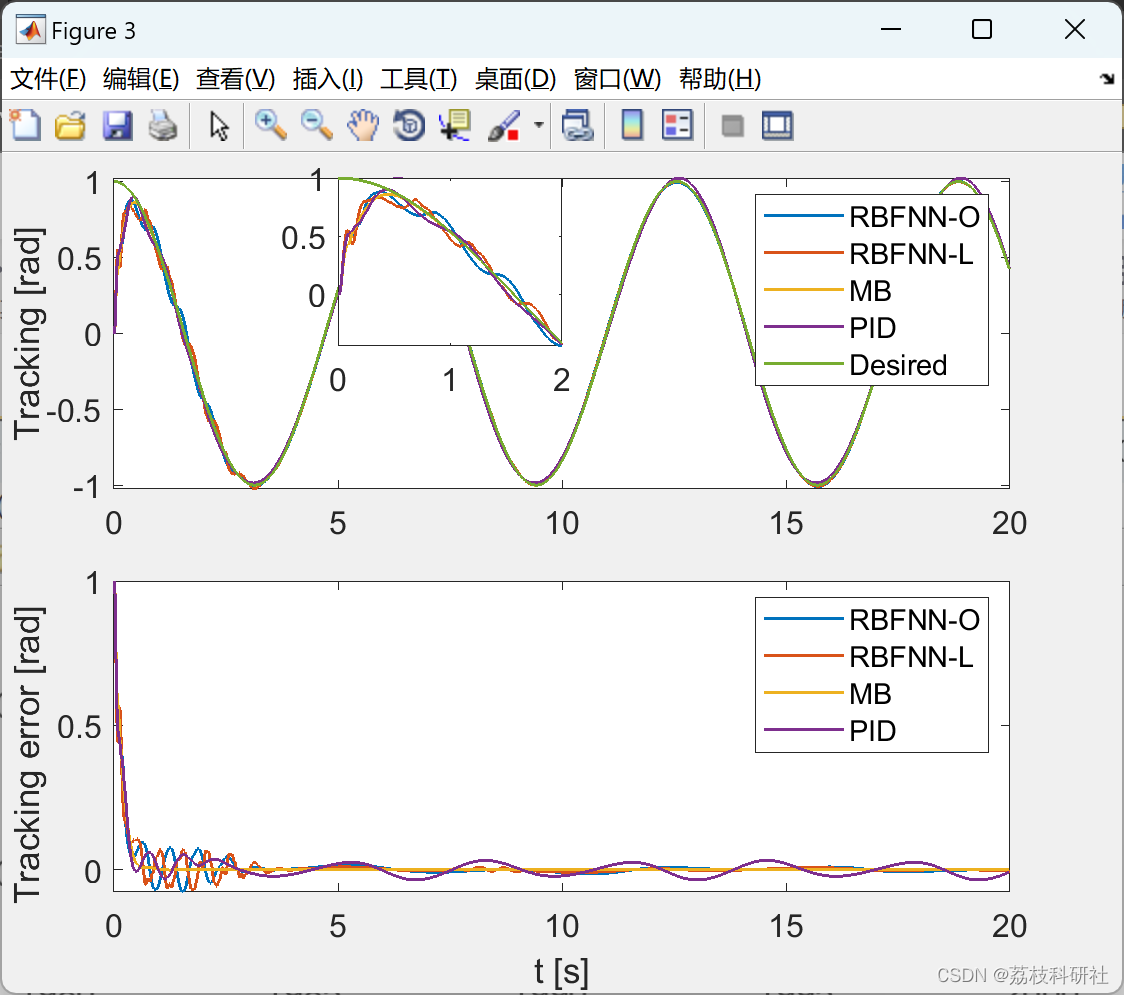
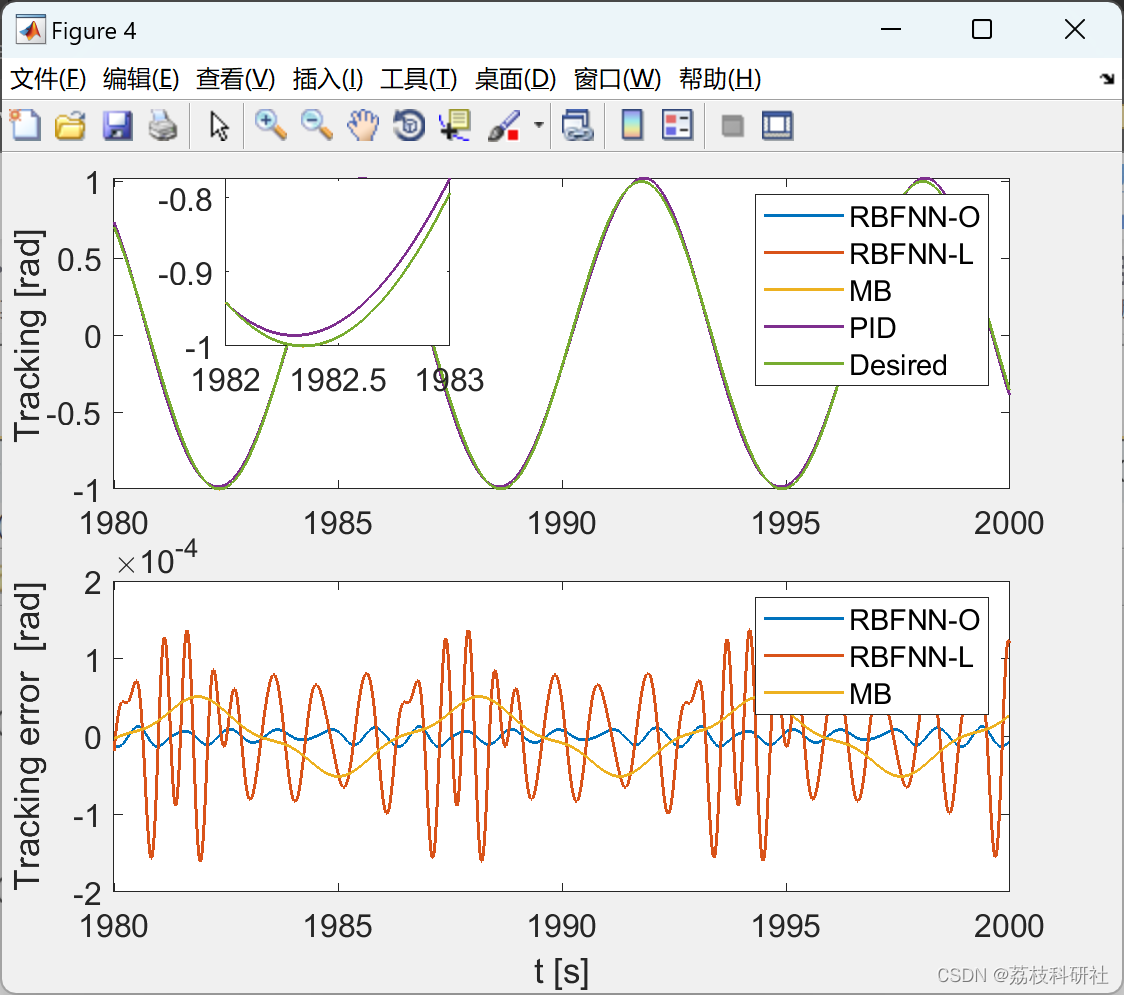
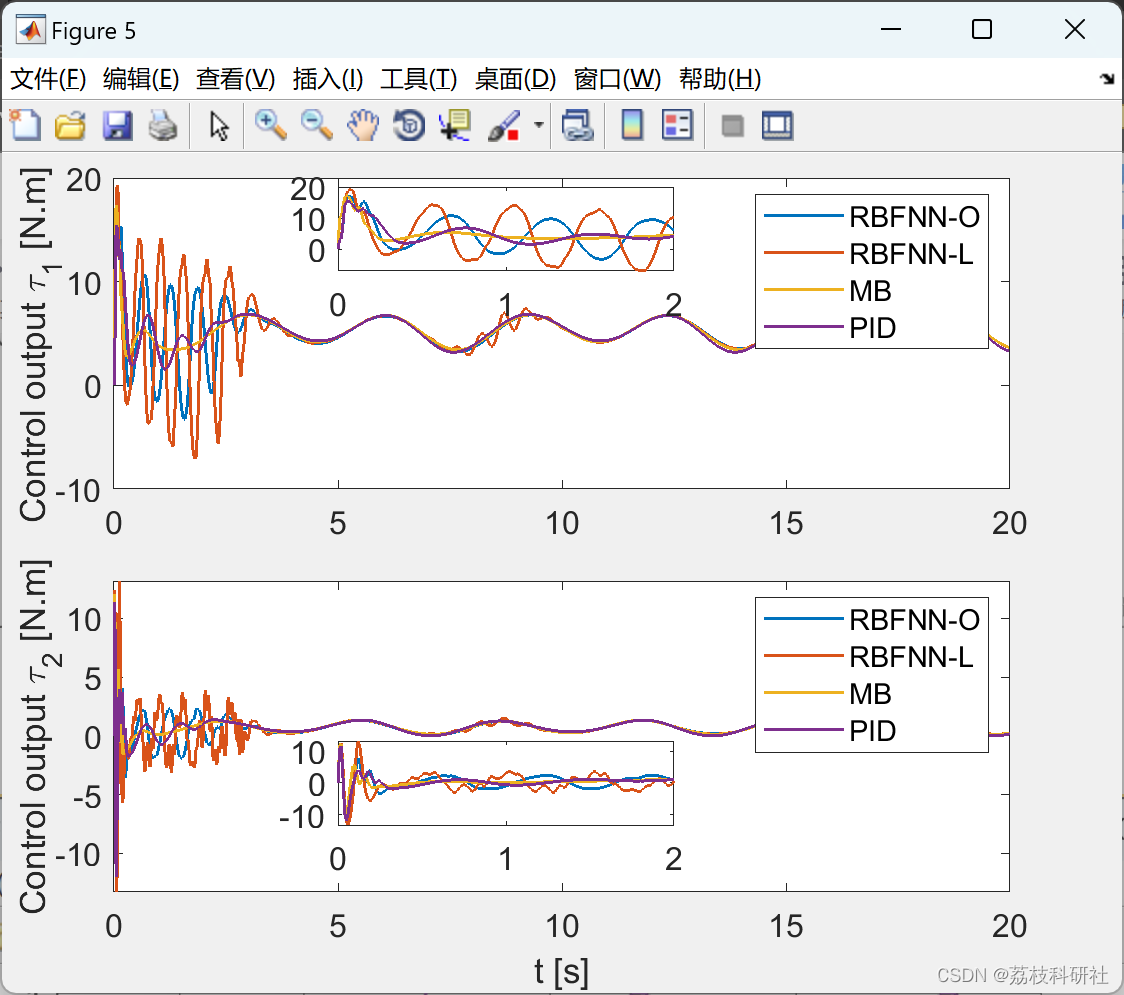
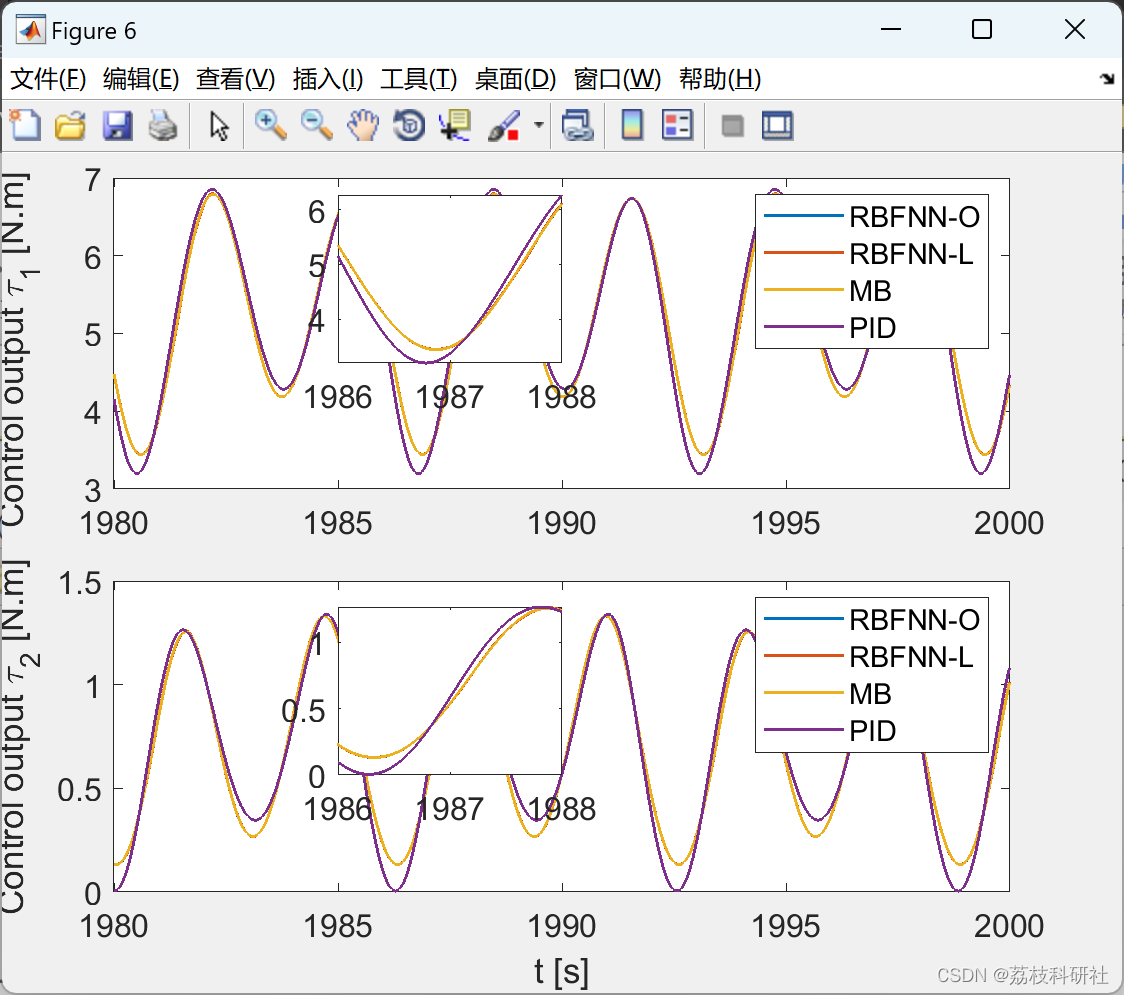
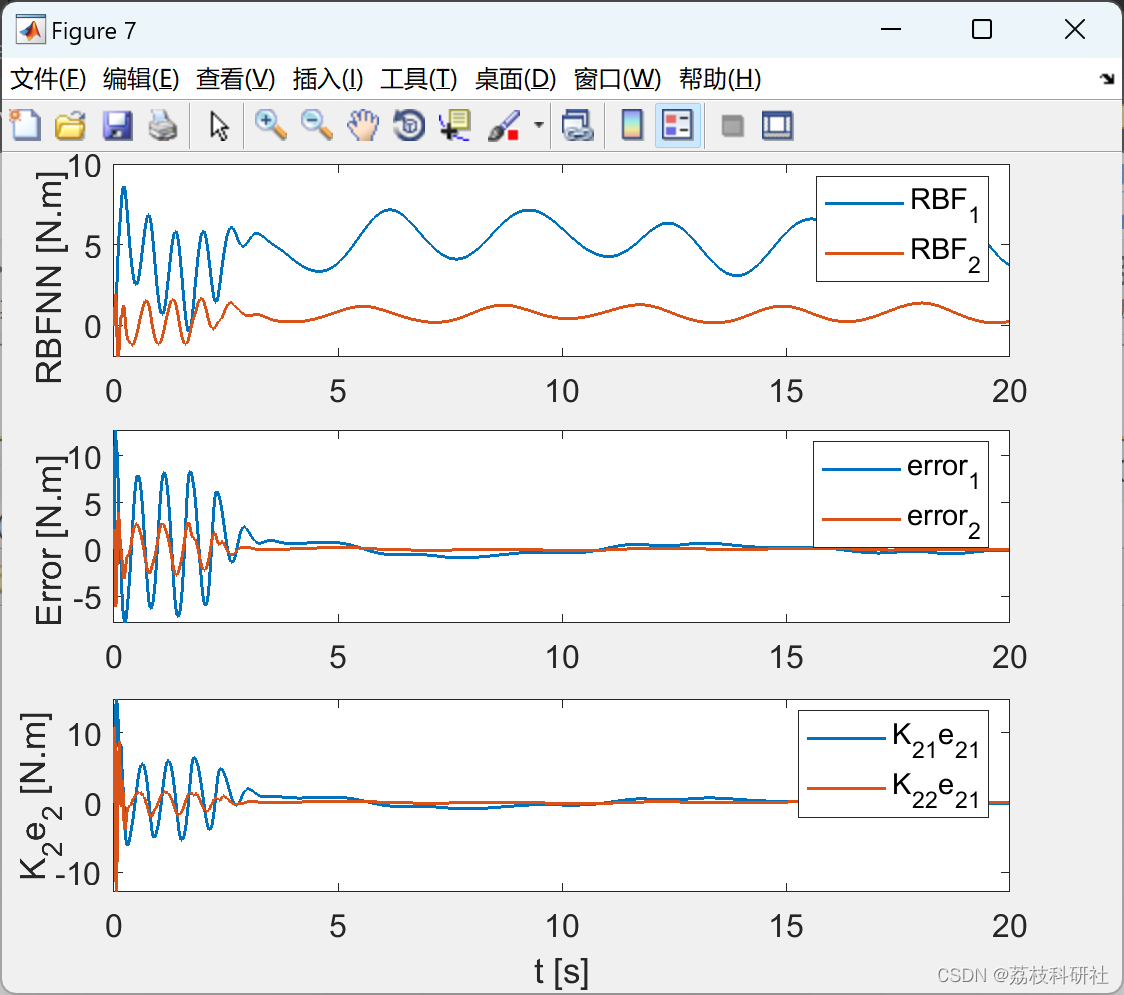
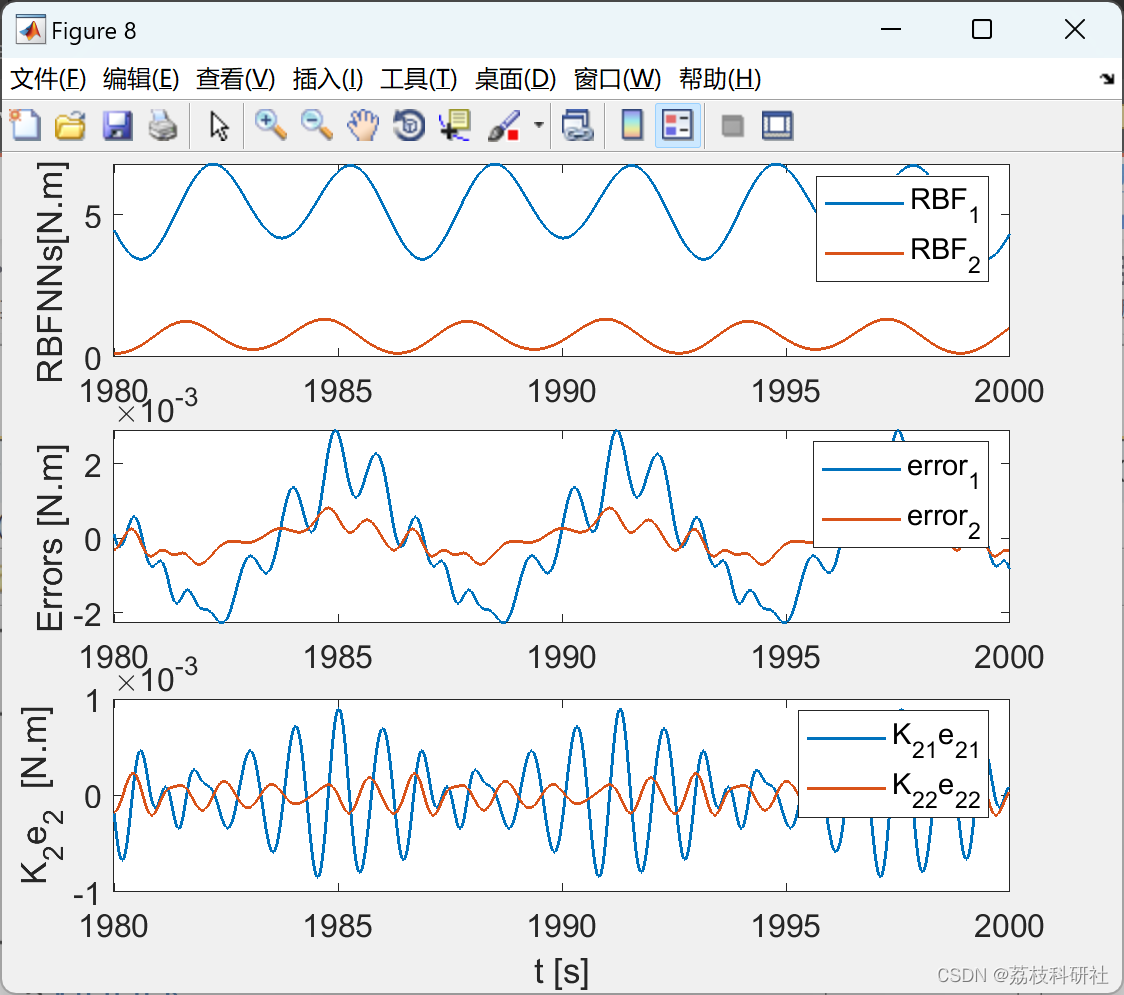
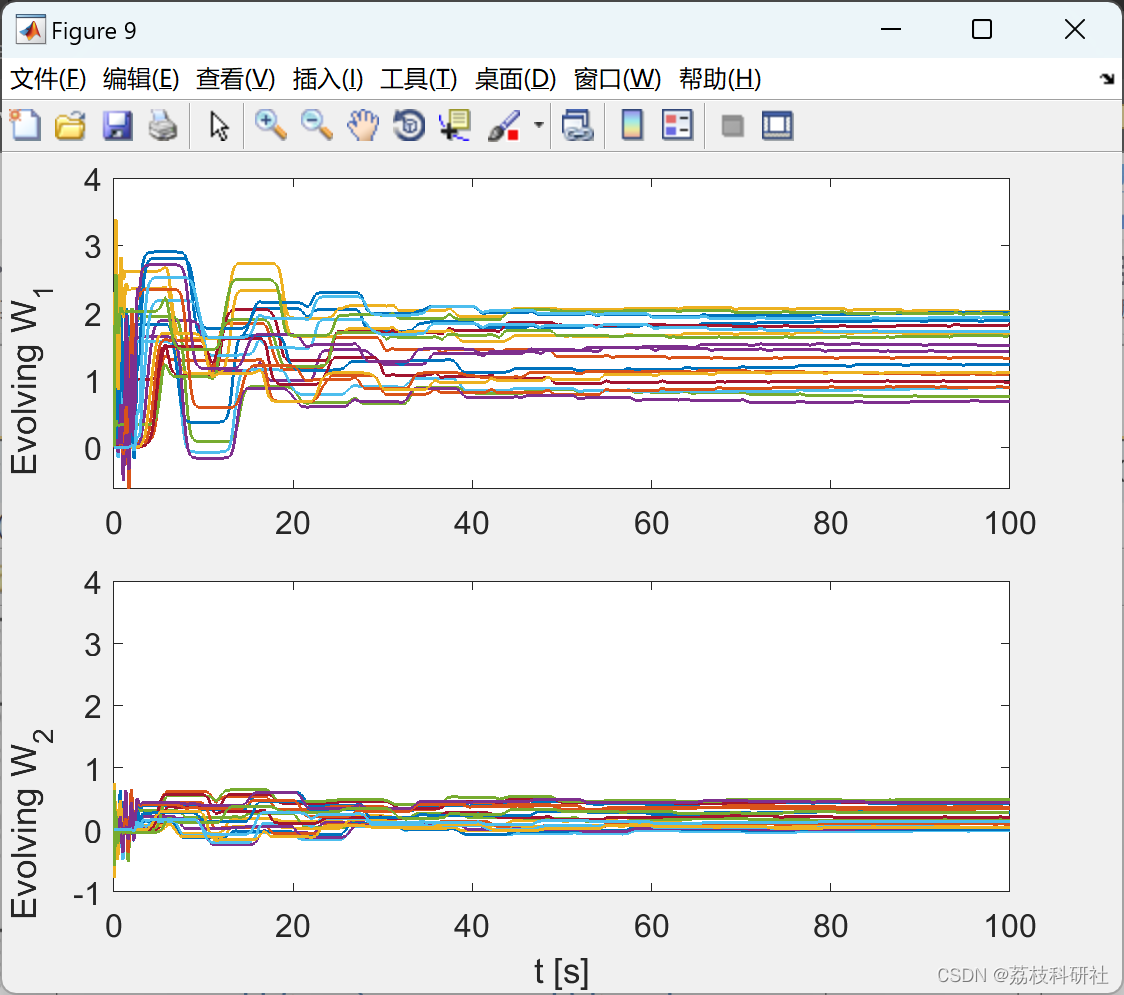
📚2 运行结果
增强型PID-自适应-前馈-神经网络控制研究(Matlab代码实现)_哔哩哔哩_bilibili
2.1 RBFNN_Optimized_hideen_node_20
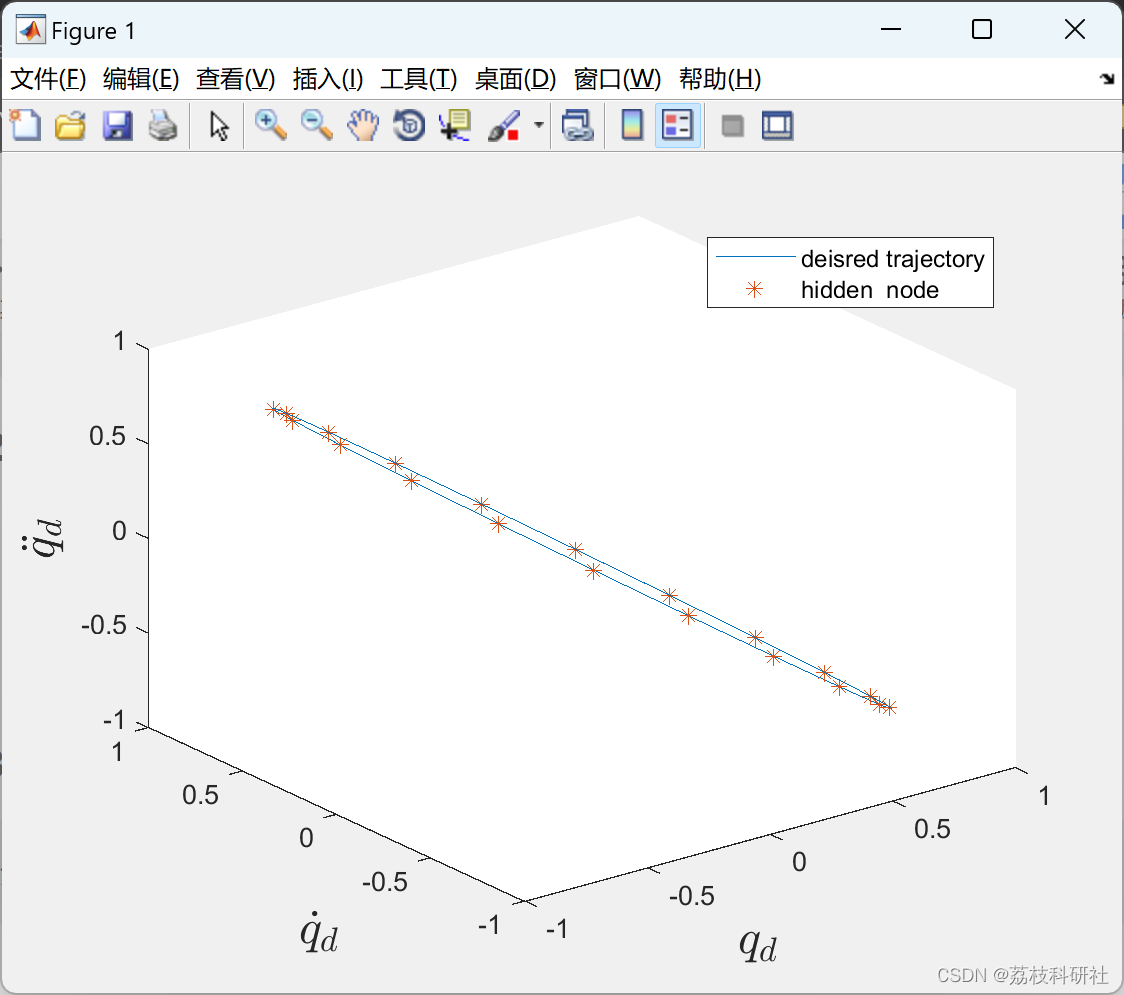
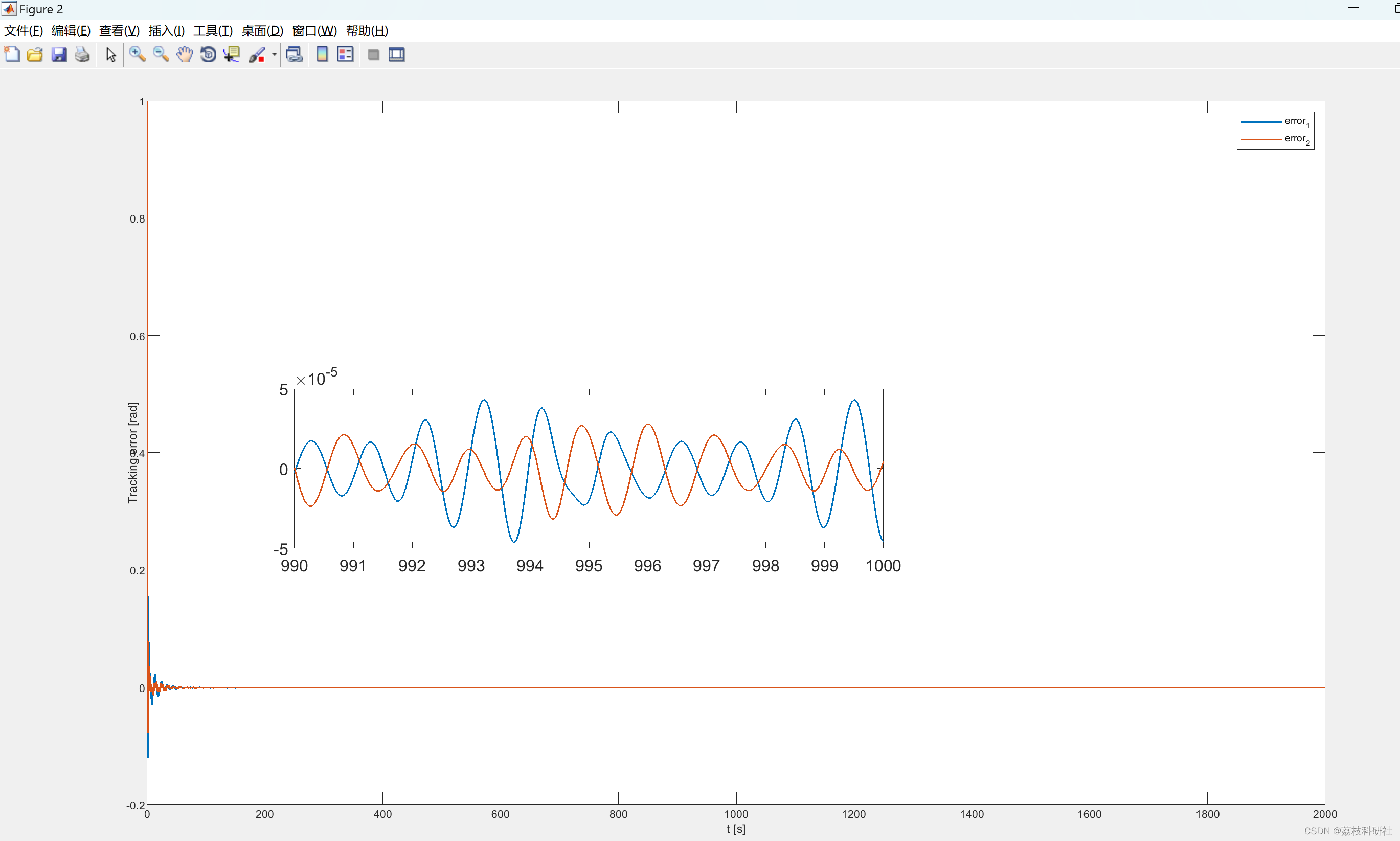


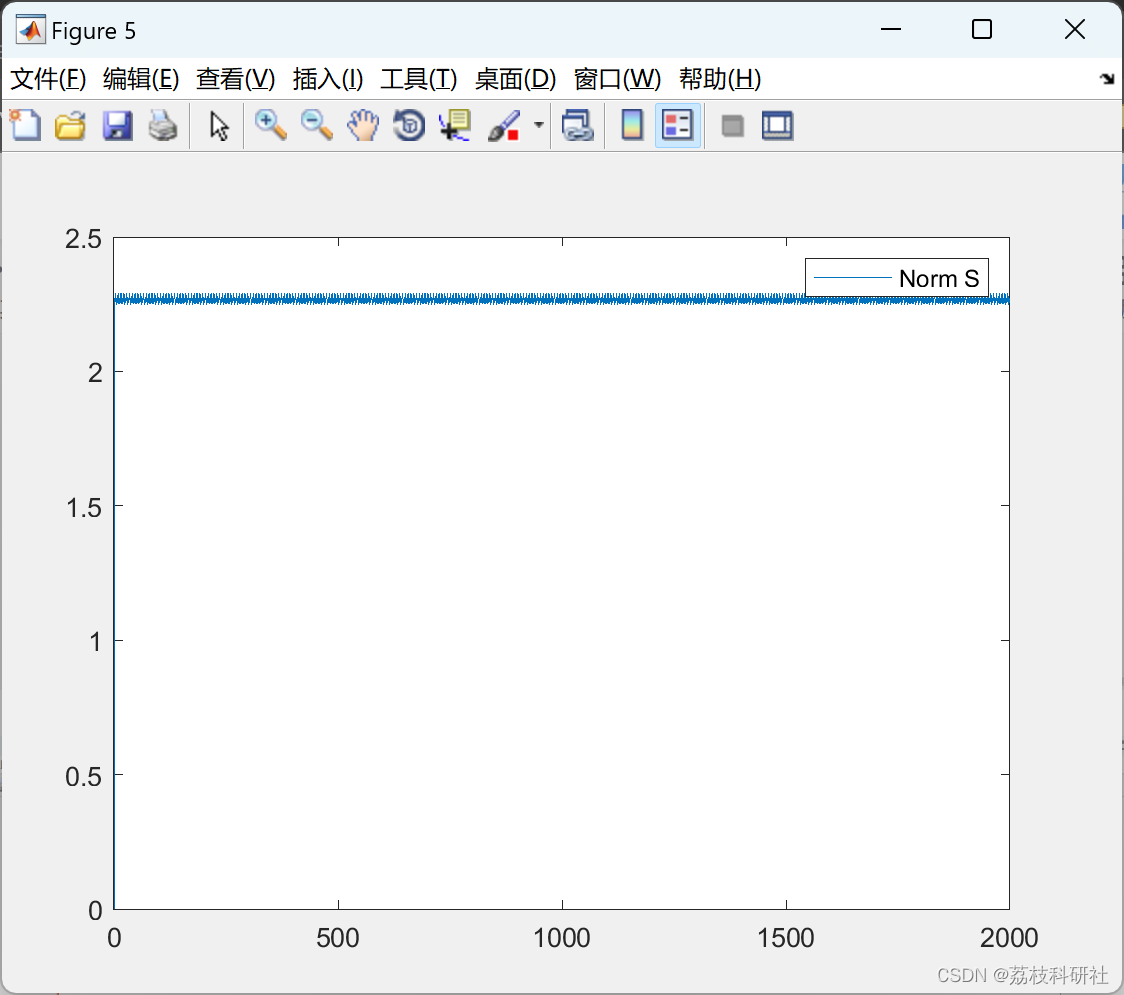
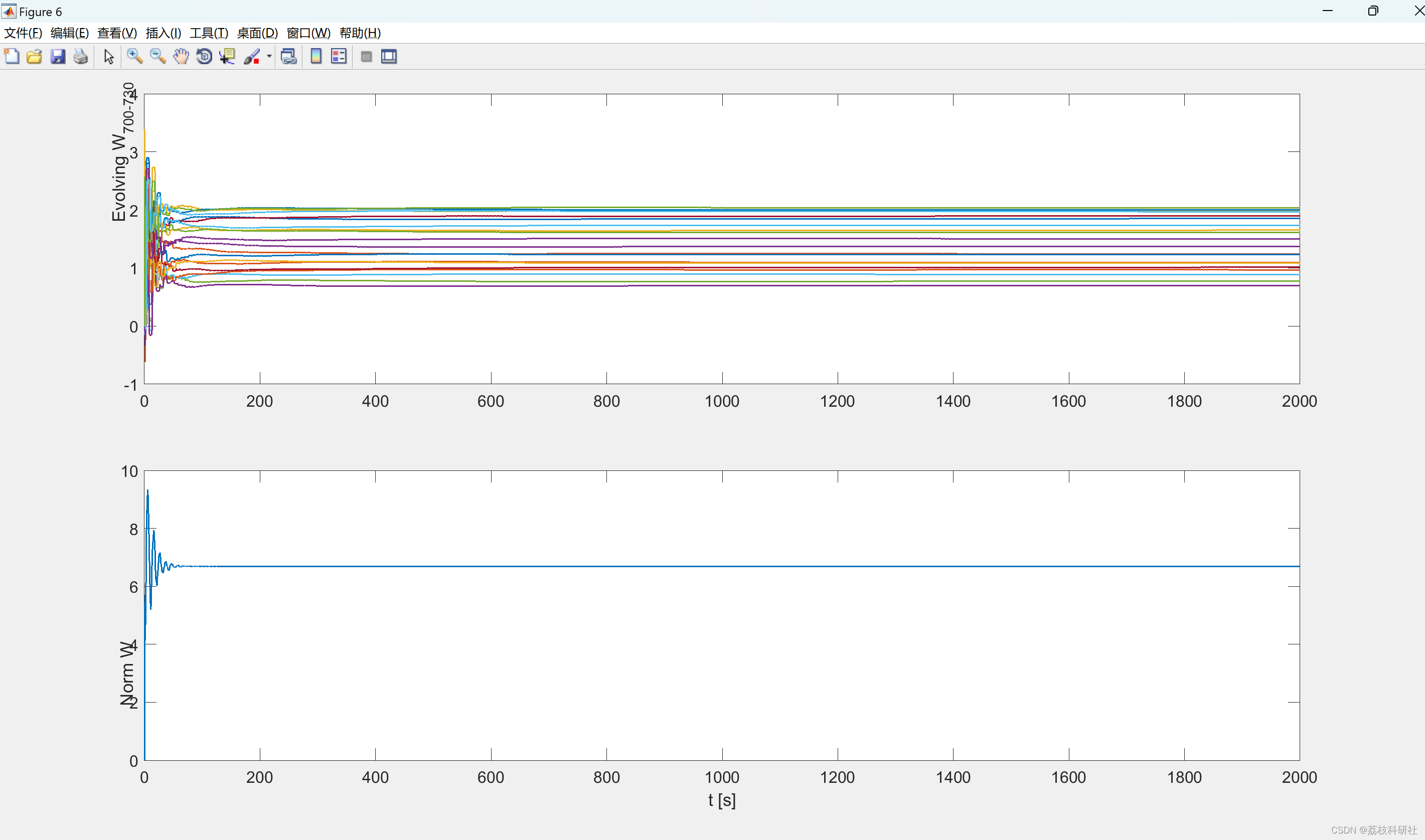


2.2 RBFNN_Lattice_hideen_node_3_6
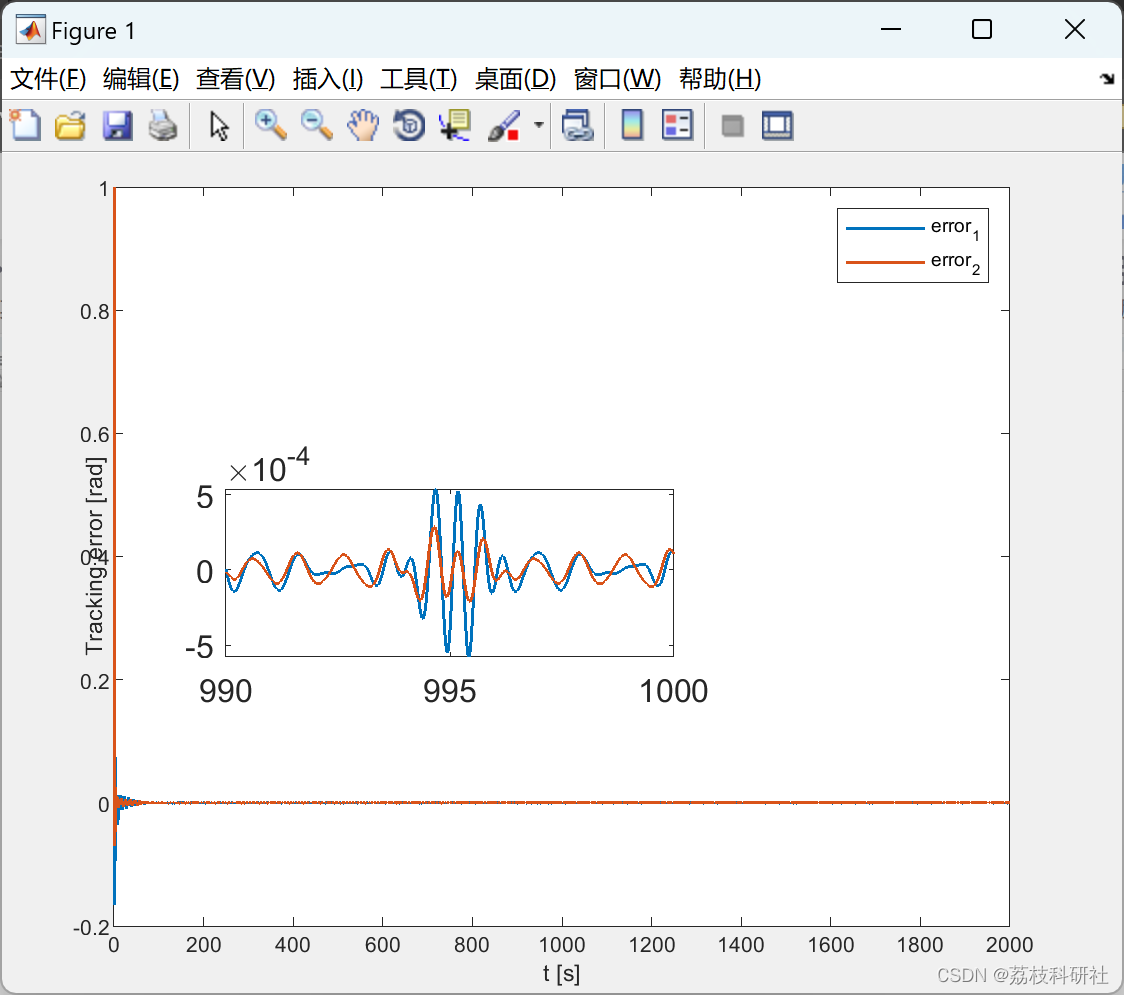
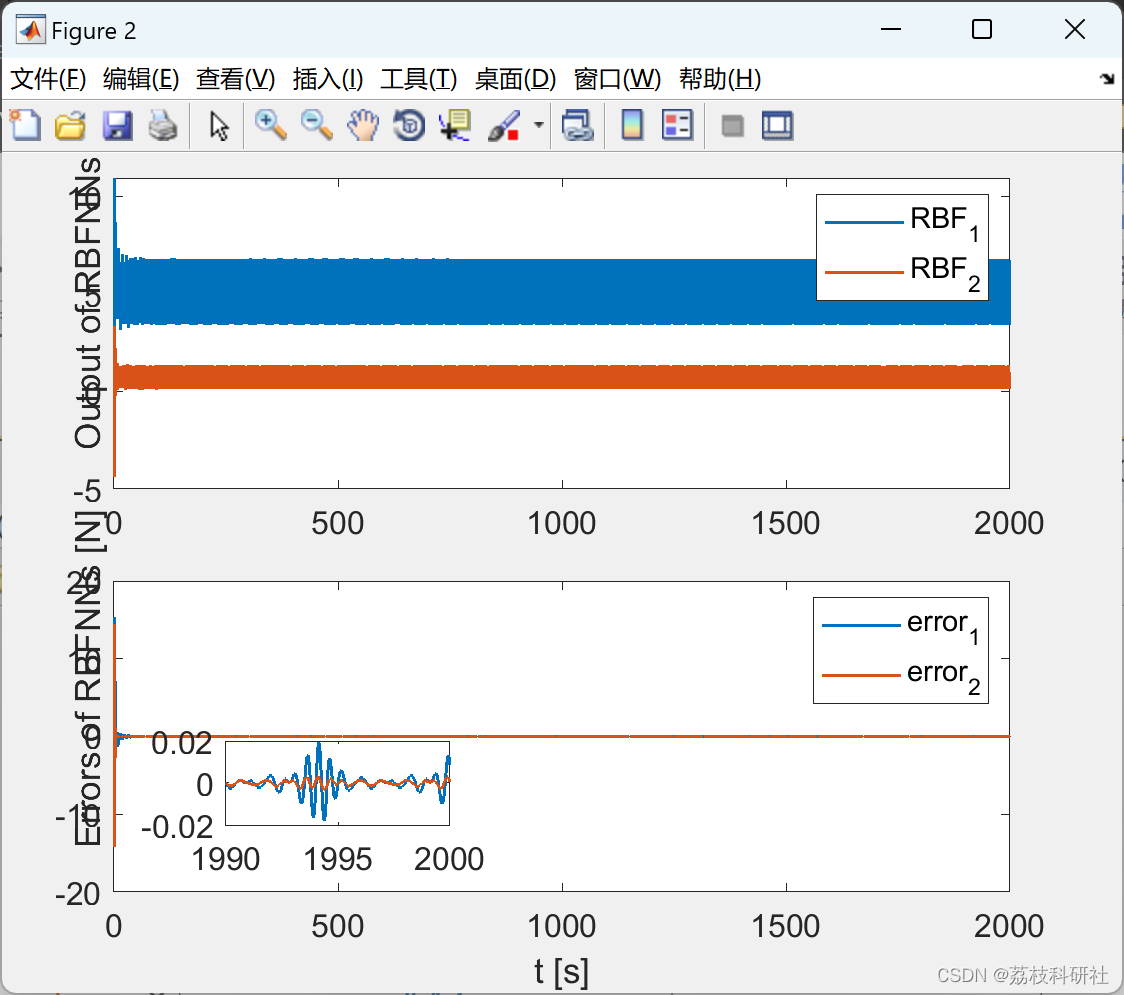
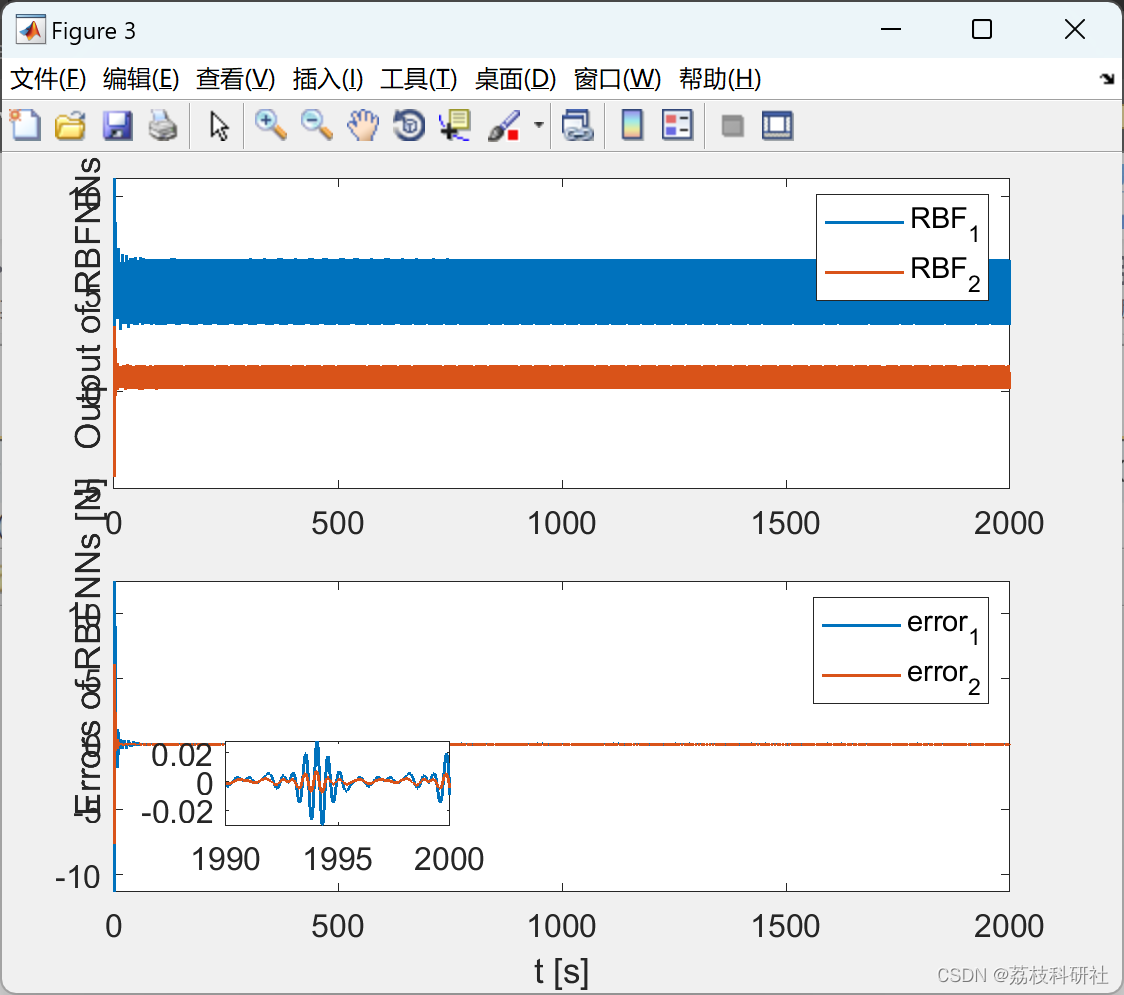

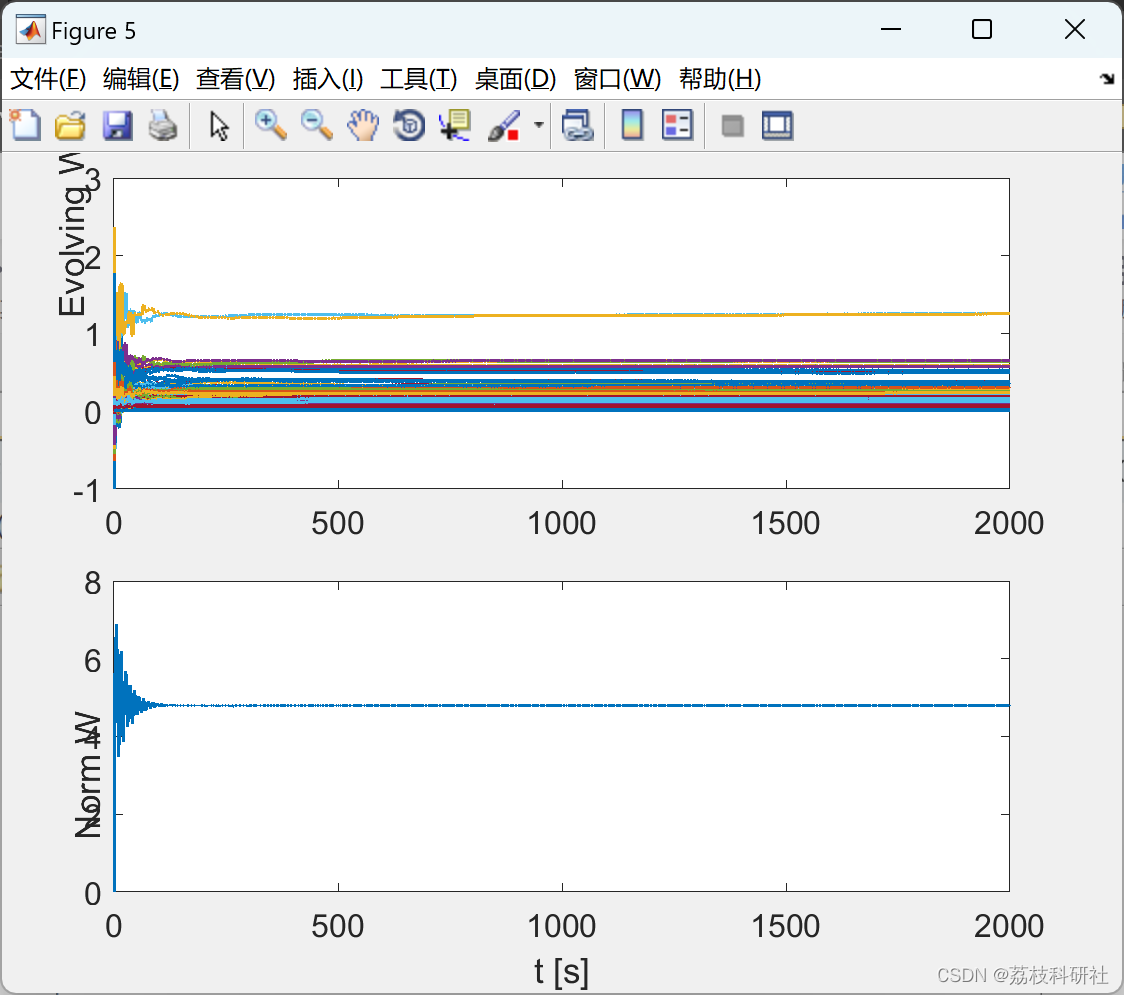
2.3 PID
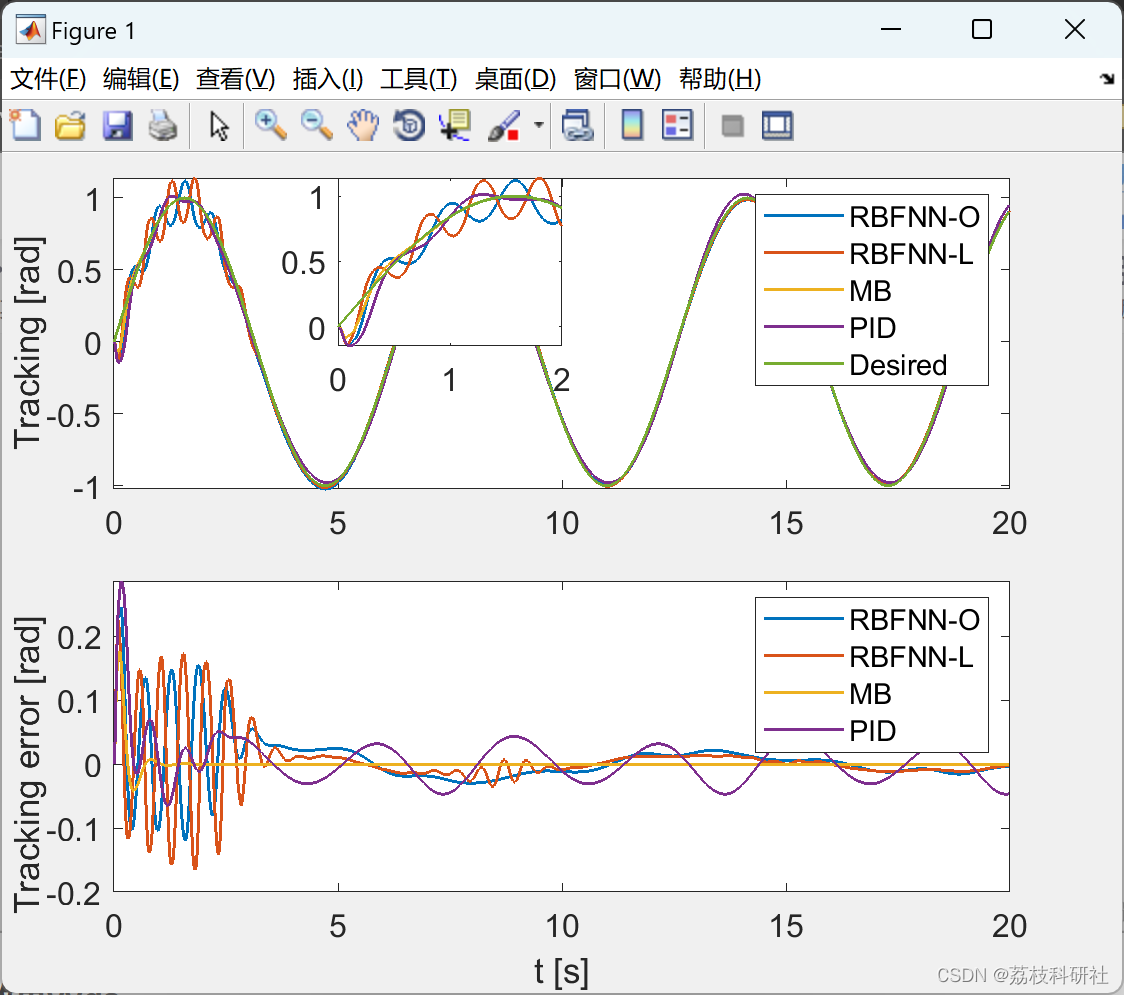
2.4 效果yyds
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。





















 2527
2527

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








