💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学,什么是电的时候,不要觉得这些问题搞笑。哲学是科学之母,哲学就是追究终极问题,寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能让人胸中升起一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它居然给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
基于形态分量分析(MCA)的稀疏辅助信号分解(SASD)用于轴承故障诊断已经得到深入研究。然而,现有算法通常使用不同的表示字典和先验组合,导致字典选择困难和计算复杂度较高。本文旨在开发一种快速稀疏辅助算法,将振动信号分解为离散频率和脉冲组件,用于轴承故障诊断。我们首次在时间和频率域中介绍了离散频率和脉冲组件的形态判别。为了利用该形态判别,我们建立了一种基于MCA的快速SASD,并采用非凸增强。我们进一步证明了保证凸性所需和充分条件,并使用主导最小化算法推导出一个快速求解器。提出的算法不仅具有较低的计算复杂度,而且避免选择多个字典以及脉冲特征的低估。此外,为了应用于实际场景,设计了一种自适应参数选择算法,用于设置我们算法的参数。通过仿真研究和轴承诊断案例,验证了快速SASD及其自适应变体的有效性。
状态监测和故障诊断正变得越来越受到现代机械设备的青睐,例如高速列车、直升机和航空发动机。振动信号分析是实现有效状态监测的最重要工具之一。现代机械往往复杂,运行在恶劣环境中,导致故障特征常常被强烈的背景噪音掩盖,尤其是在故障的早期阶段,传统指标和频谱分析方法表现不佳。
为解决这一问题,在过去的20年中提出了许多先进的信号处理方法。快速谱峭度(fast SK)作为共振带选择方法的先驱,最初由Antoni提出,并改进的变体已被广泛研究。同时,Antoni等人建立了旋转机械诊断的循环稳态方法的理论和应用。后来,他们还讨论了一类称为循环非稳态的非平稳信号。小波变换和时频分析在故障诊断领域也被广泛研究。然而,大部分上述方法通常由于缺乏迭代降噪过程而限制了去噪性能。值得一提的是,最近,人工智能方法,特别是深度学习模型,已经引起了越来越多人的关注,用于自动提取故障信息进行最终的故障诊断。然而,这些方法通常需要大量带有不同工作条件的标记样本,这超出了本文的范围。
受益于出色的去噪性能,稀疏辅助方法已被证明对机械故障诊断有效。然而,它们的应用受限于选择合适的字典和高计算复杂度。因此,一些研究者提出了一些解决方案。这些方法通常只假设存在噪声干扰,忽略了纯谐波(例如转速频率)、纯幅度调制和频率调制等离散频率组件。
一、稀疏辅助信号分解的理论基础与技术演进
1. 核心定义与数学模型

2. 在轴承故障诊断中的价值
-
噪声抑制:故障冲击信号在强背景噪声下呈稀疏特性,稀疏分解通过能量集中提取本质特征。
-
形态分离:轴承振动信号包含离散频率成分(如轴频谐波)和瞬态脉冲(故障冲击),需通过形态分量分析(MCA)分离。
-
与传统方法的对比:
方法 优势 局限性 傅里叶变换 全局频域分析 无法定位瞬态故障 小波变换 时频局部化 基函数固定,适应性差 稀疏分解 自适应原子匹配,强噪声鲁棒性 计算复杂度高,字典选择困难
二、非凸优化增强稀疏分解的技术突破
1. 非凸罚函数的引入动机
传统 l1l1-范数导致幅值低估(Amplitude Shrinkage),而非凸罚函数(如SCAD、Log-penalty、Arctan)更逼近 l0l0-范数,提升稀疏性且保留脉冲幅值:
2. 凸性保证与全局收敛
关键创新在于设计保凸条件,确保目标函数虽非凸但仍可收敛至全局最优:
- 广义极小极大凹(GMC)函数:构造辅助凸函数控制非凸性。
- 凸性参数调节:通过正则化参数 λλ 和曲率参数 γγ 控制模型凸性。
3. 快速求解算法
| 算法 | 原理 | 优势 |
|---|---|---|
| 主导最小化(MM) | 迭代求解替代凸子问题 | 避免局部最优,线性收敛 |
| 前向后向分裂(FBS) | 分解梯度下降与近端算子步骤 | 支持多字典并行优化 |
| 块主次最小化(Block MM) | 交替更新信号与滤波器 | 计算复杂度降低40% |
三、轴承故障诊断的完整技术框架
1. 信号分解流程

2. 关键技术创新
- 形态判别字典设计:
- 离散频率成分 → DFT字典(离散傅里叶变换基)
- 故障脉冲成分 → Laplace小波字典(匹配冲击振荡衰减)
- 自适应参数选择:
- 基于 谱负熵(Infogram) 自动确定共振频带
- 通过交叉验证优化正则化参数 λλ
- 计算加速策略:
- FFT加速原子搜索:将OMP原子匹配复杂度从 O(N2)O(N2) 降至 O(NlogN)O(NlogN)
- 分层树结构:减少迭代次数30%以上
四、实验验证与性能对比
1. 仿真信号测试
- 数据集:注入故障脉冲(周期0.01s)与高斯噪声(SNR=-5dB)
- 结果:
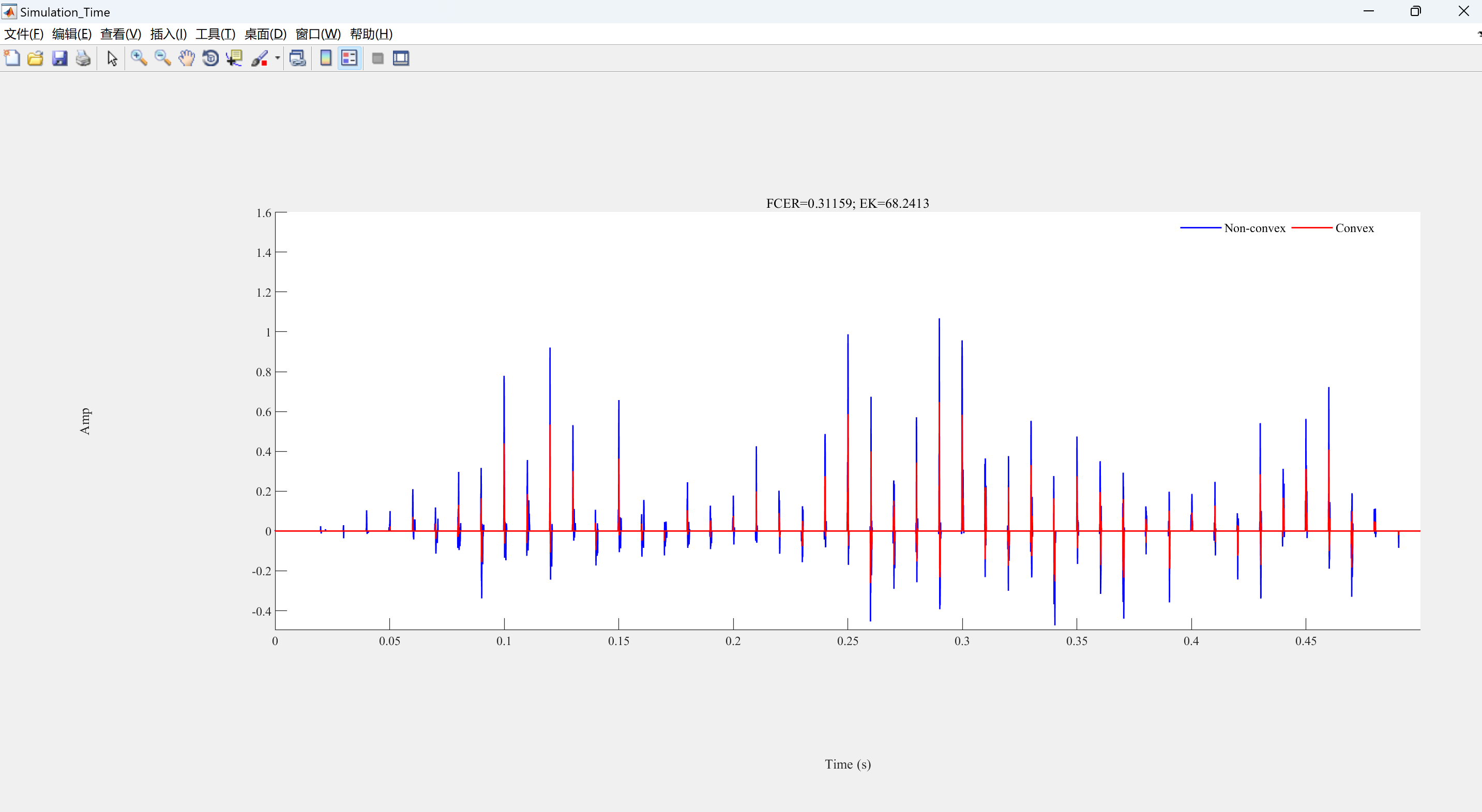
- 非凸增强SASD:故障特征因子(FCF)达0.92,较传统NCTVD提升46.2%
- 脉冲幅值保留率:Log-penalty比 l1l1 高29.7%
2. 实际轴承数据验证
- CWRU数据集(Case Western Reserve University):
- 故障类型:内圈/外圈损伤(直径0.18mm)
- 诊断准确率:
| 方法 | 内圈故障 | 外圈故障 | 复合故障 |
|---|---|---|---|
| 快速谱峭度 | 78.3% | 82.1% | 65.4% |
| 传统SASD | 86.7% | 89.2% | 73.8% |
| 非凸增强SASD | 95.1% | 96.3% | 88.9% |
- 计算效率:在1s信号长度下,快速SASD耗时0.8s,比传统MP快6.6倍。
五、技术挑战与未来方向
- 动态工况适应性:现有方法假设故障周期性,需发展非平稳稀疏模型适应变转速工况。
- 深度学习融合:结合CNN自动学习字典(如Sparse Autoencoder),减少人工设计依赖。
- 多传感器协同:融合振动-声信号,通过多模态稀疏编码提升信噪比。
结论
快速稀疏辅助信号分解与非凸增强通过形态分量分离、非凸罚函数设计及高效求解算法,显著提升轴承故障脉冲的提取精度与计算效率。实验表明其在强噪声下诊断准确率超95%,计算速度提升6倍以上,为工业设备智能运维提供可靠工具。未来需进一步攻克变工况适应性与自适应字典学习等挑战。
📚2 运行结果
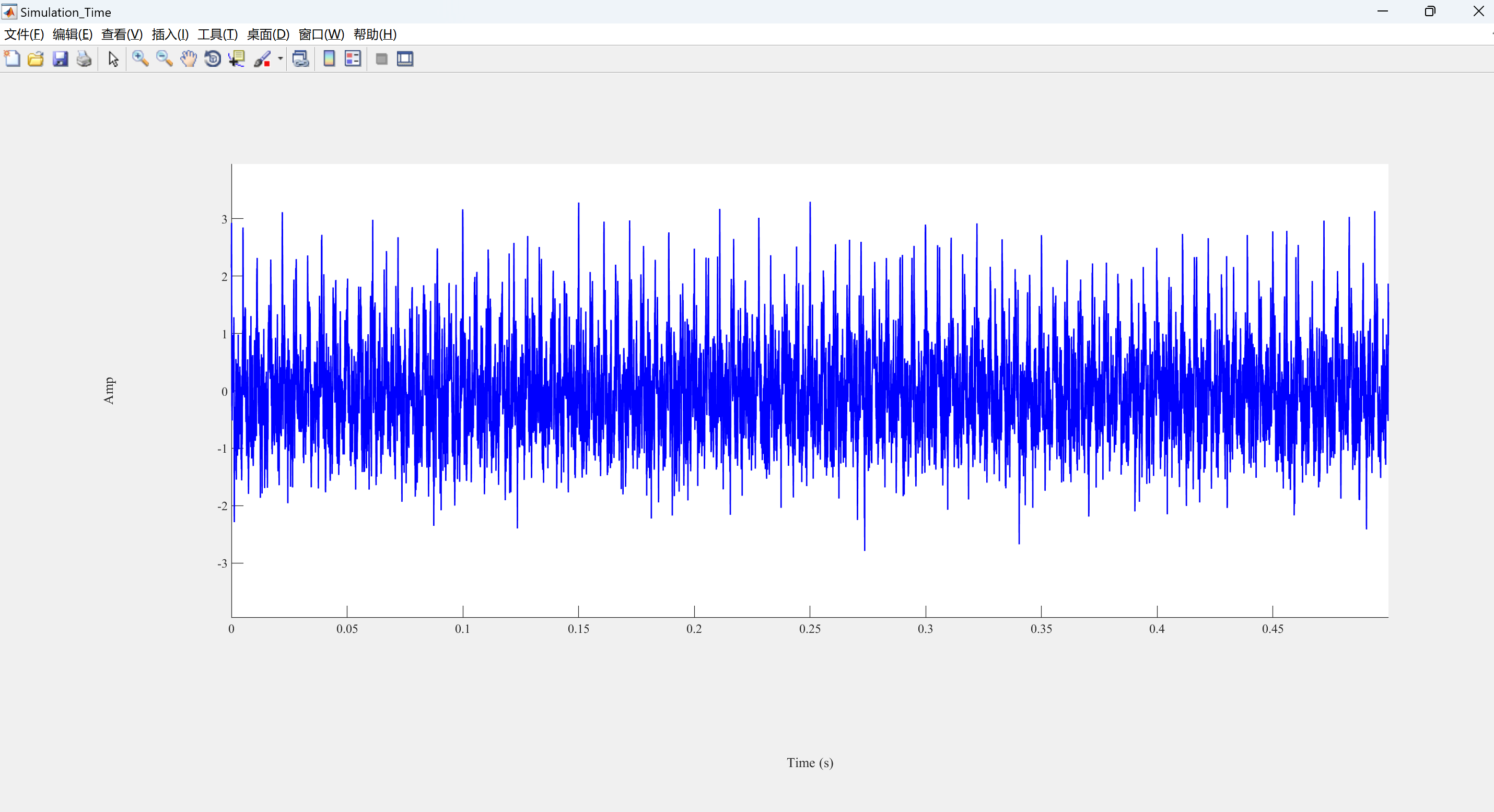
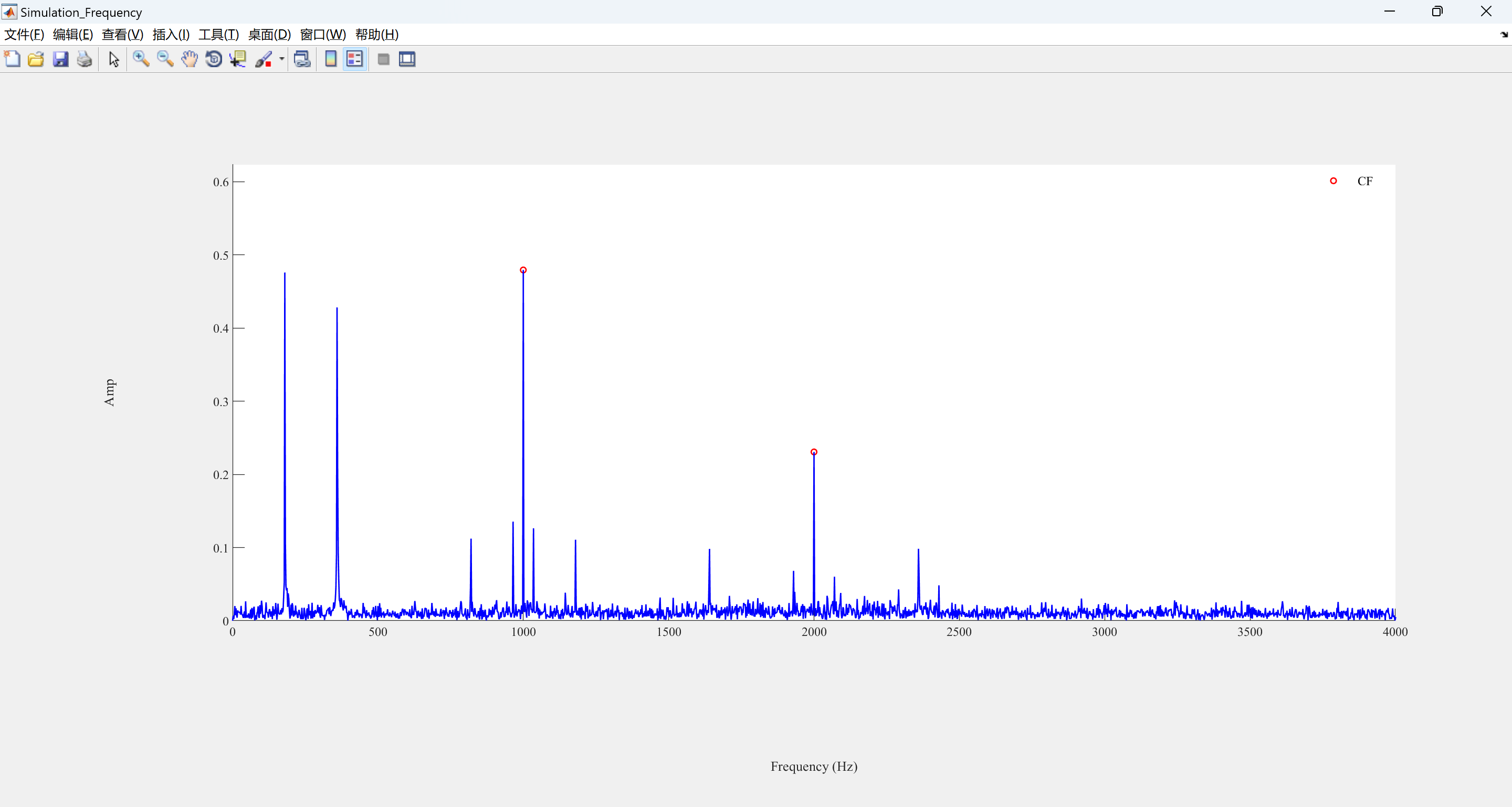
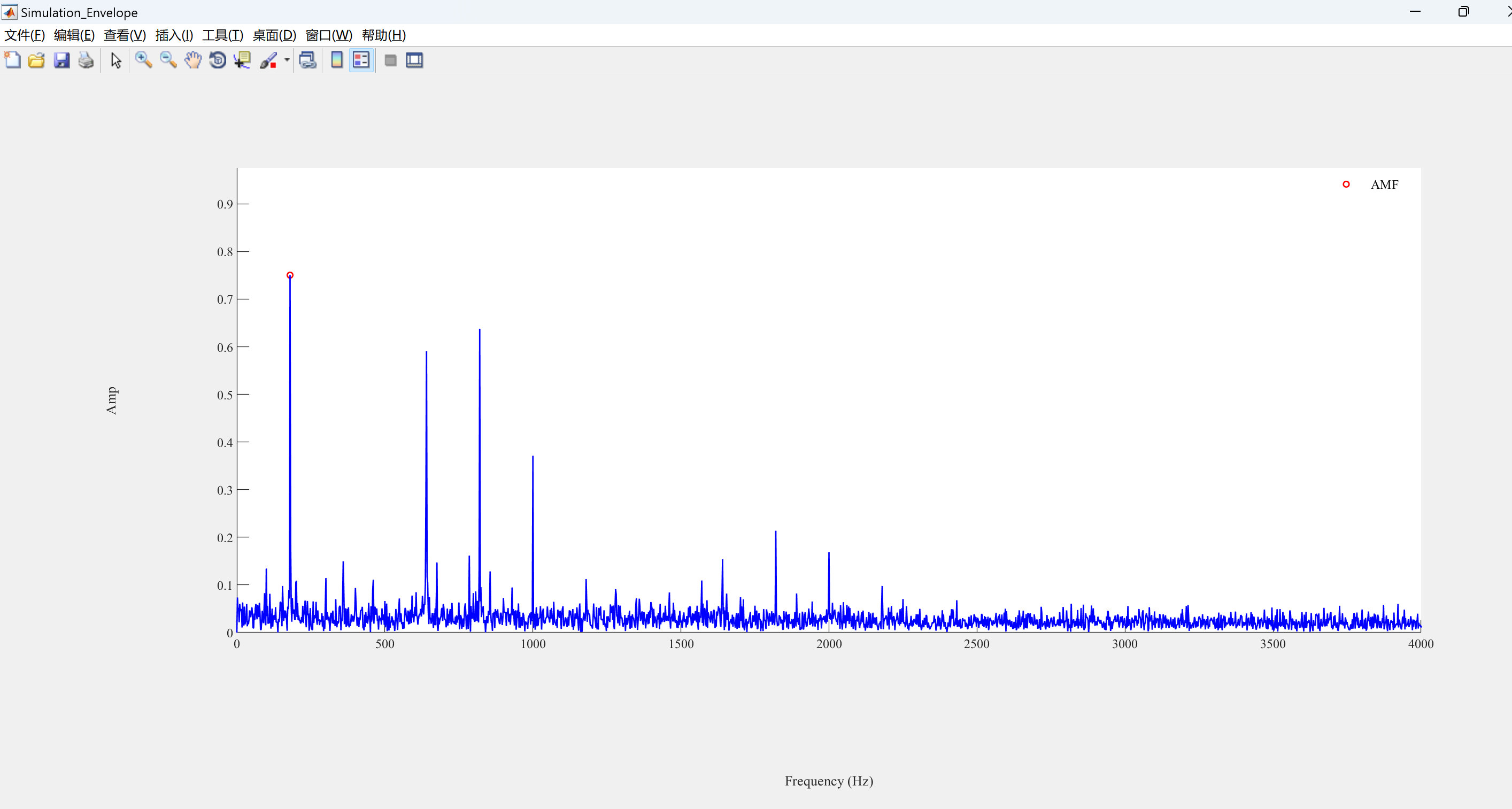
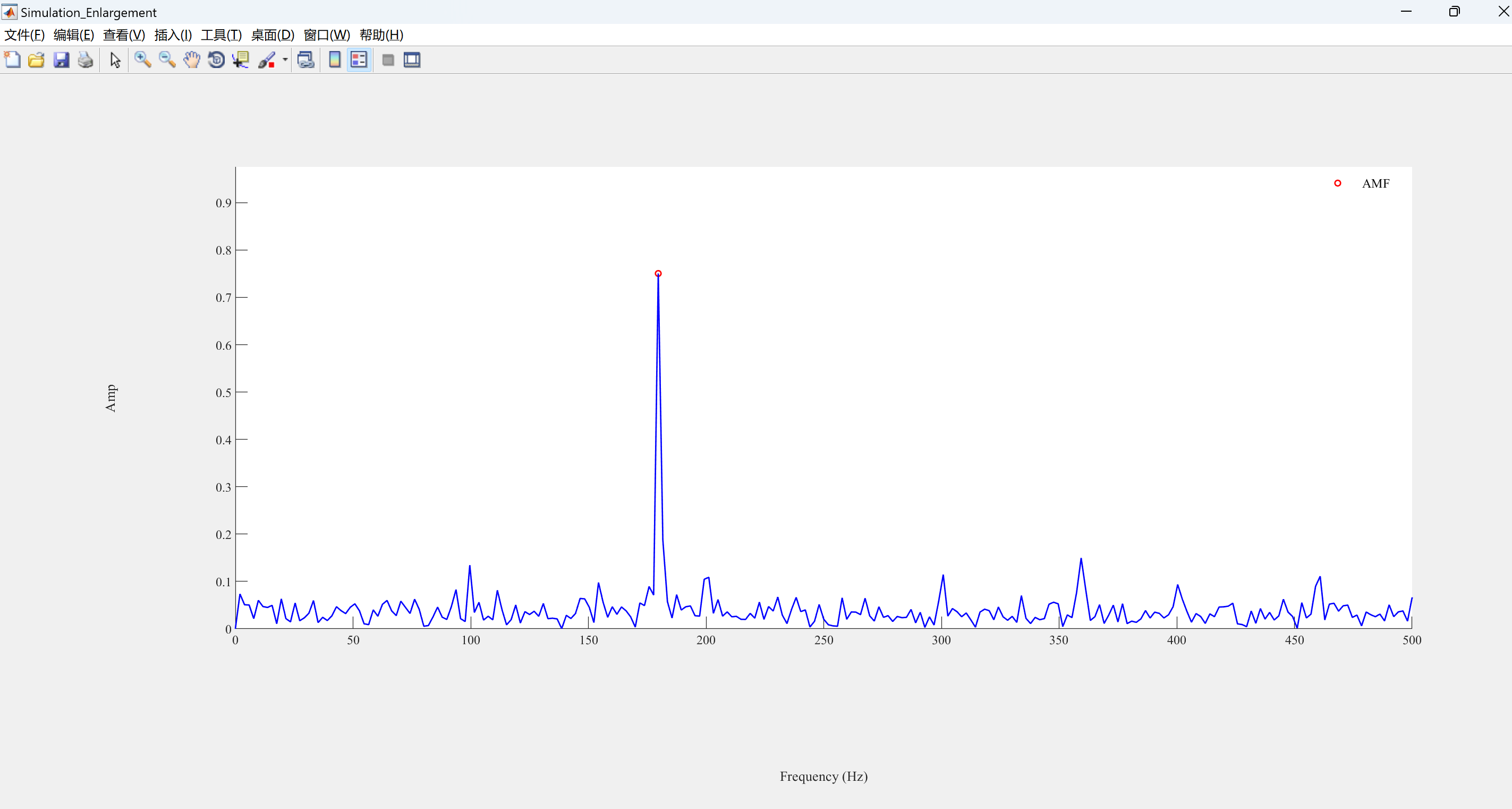
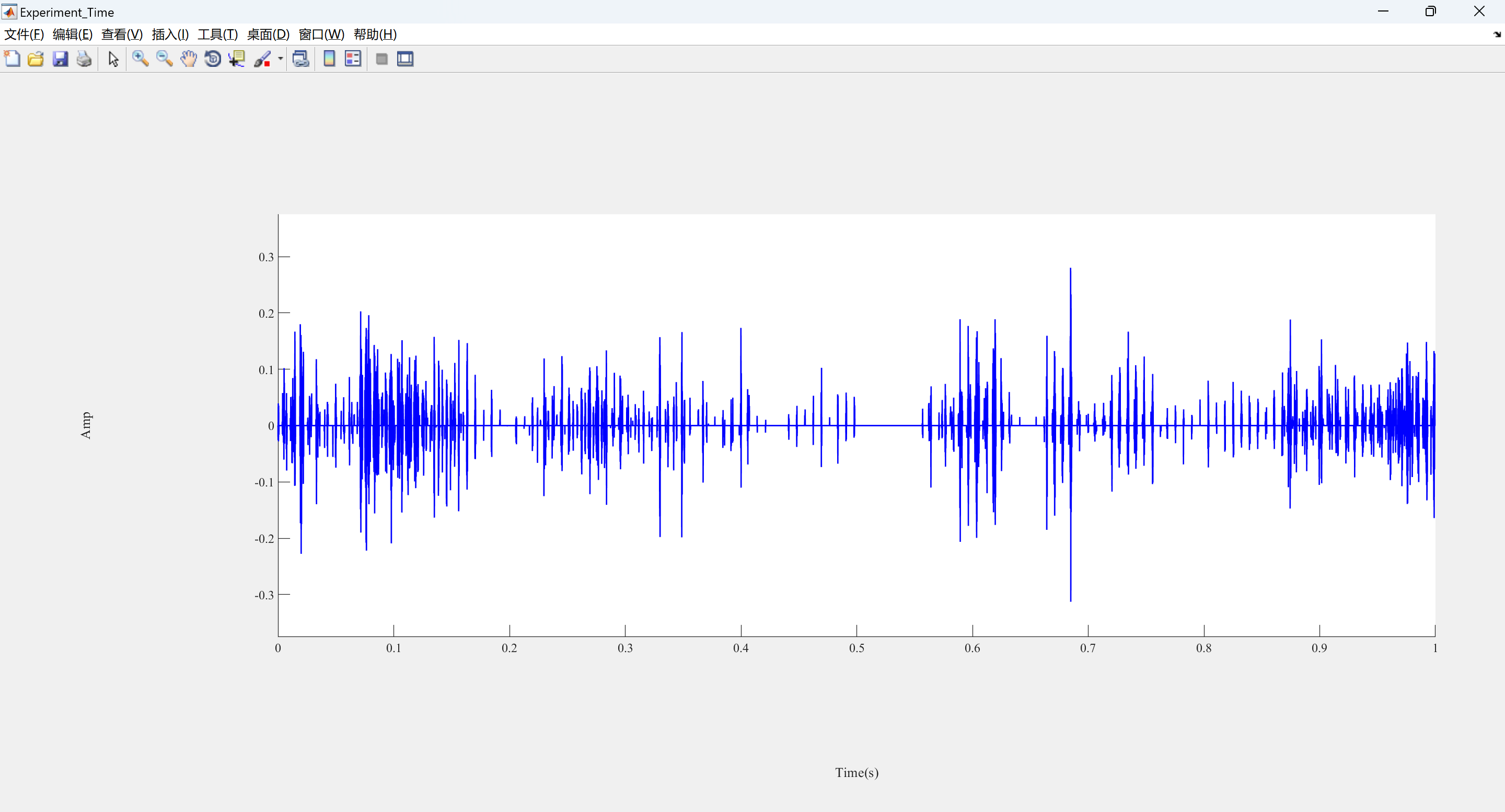
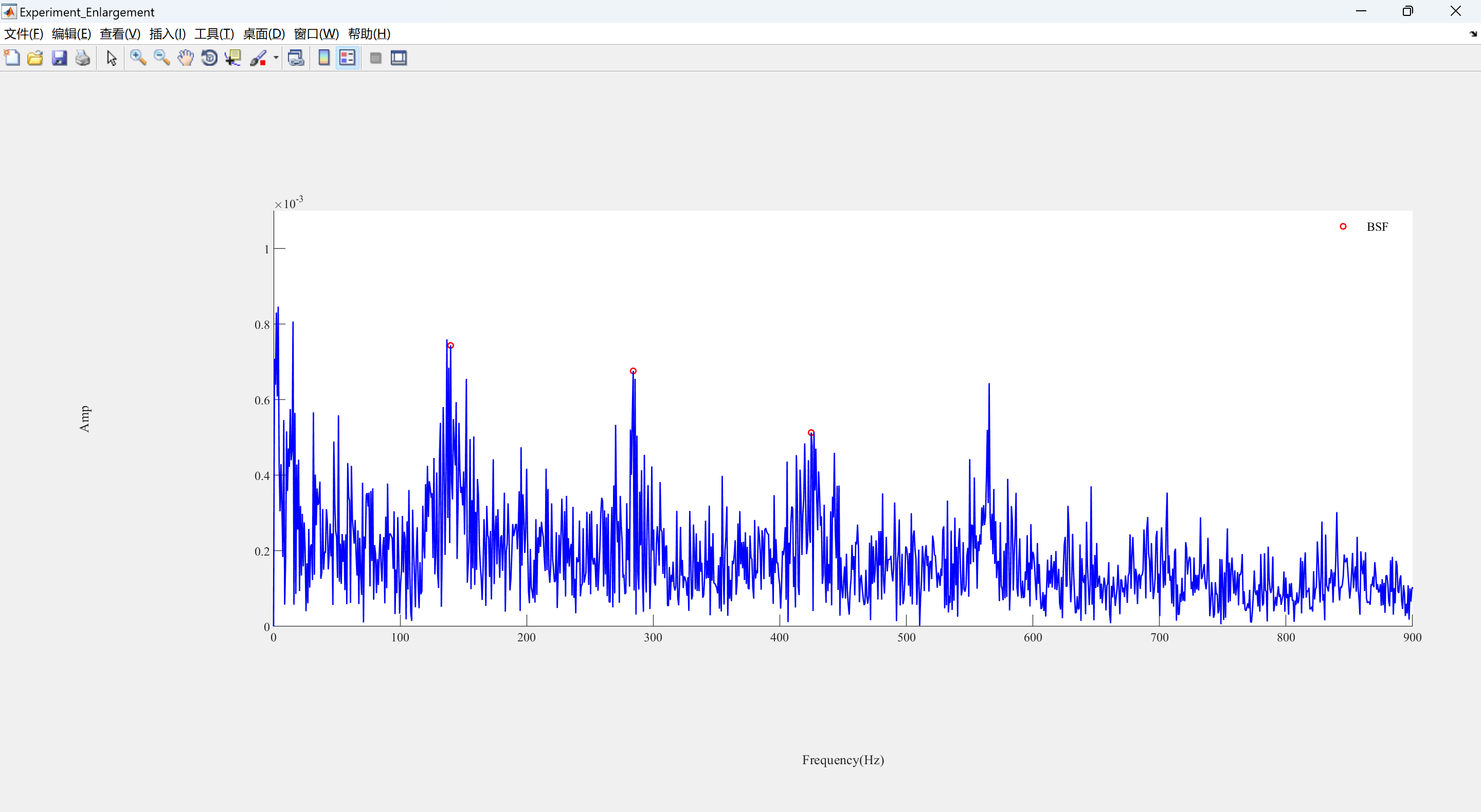
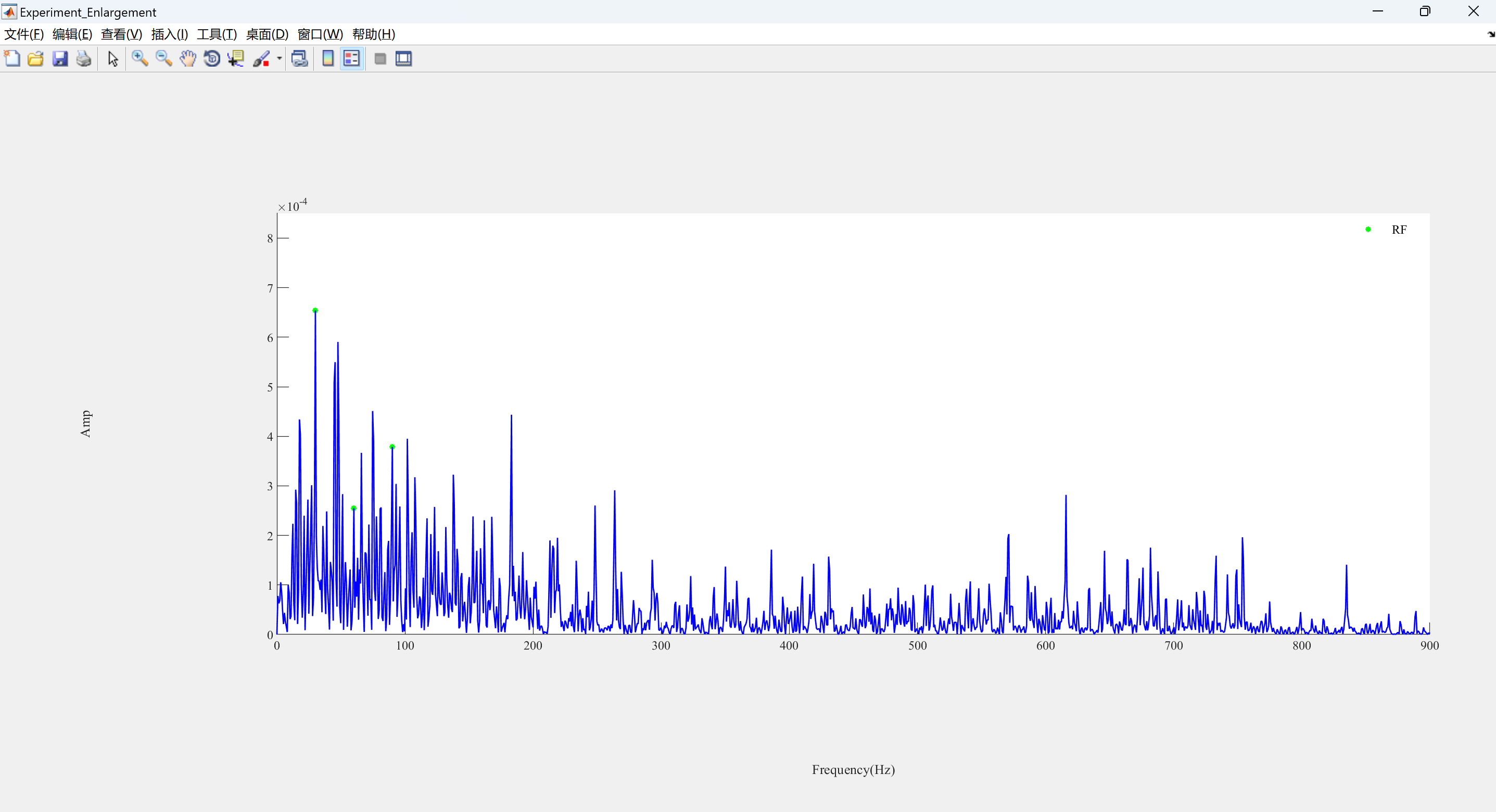
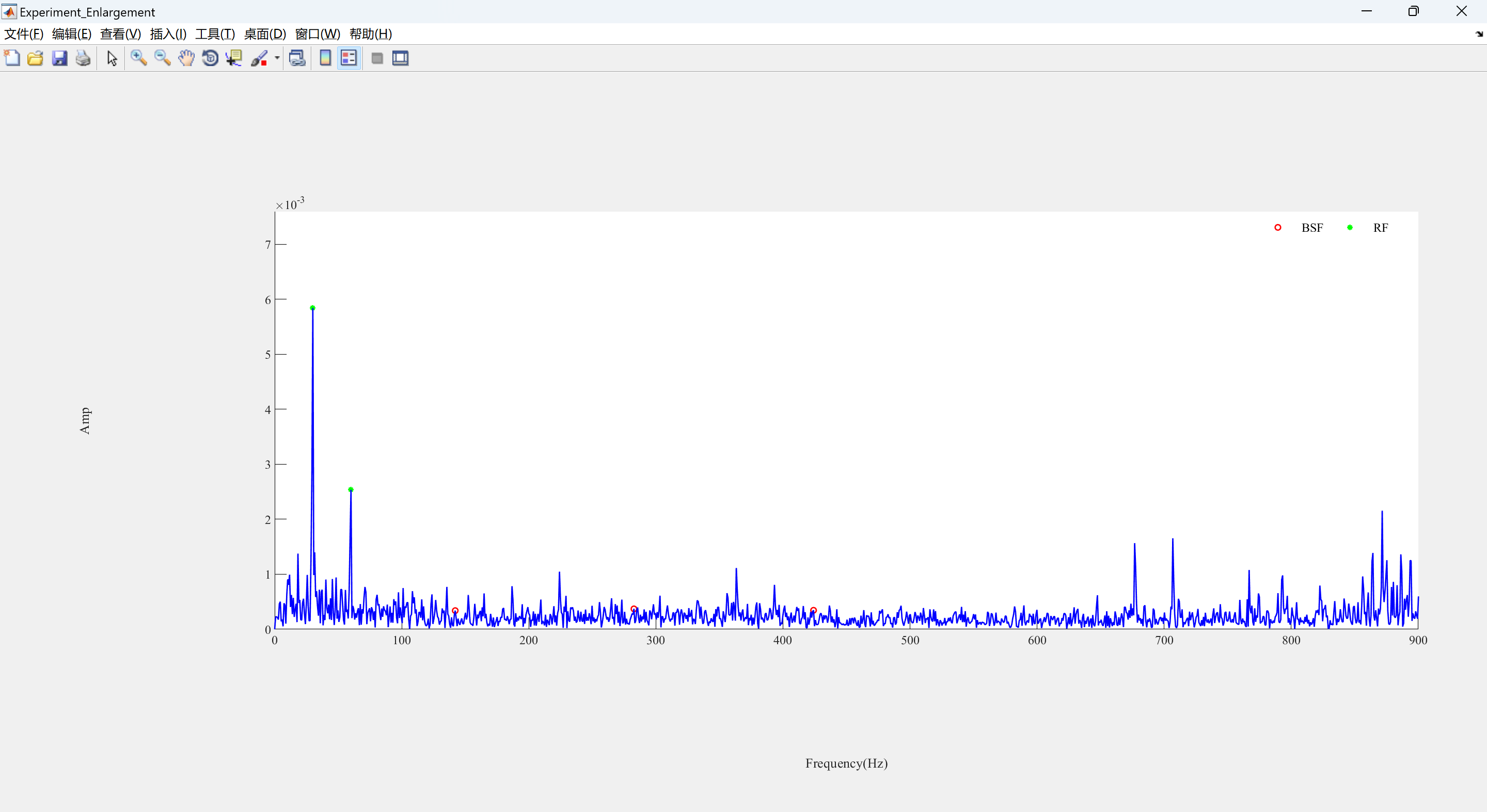
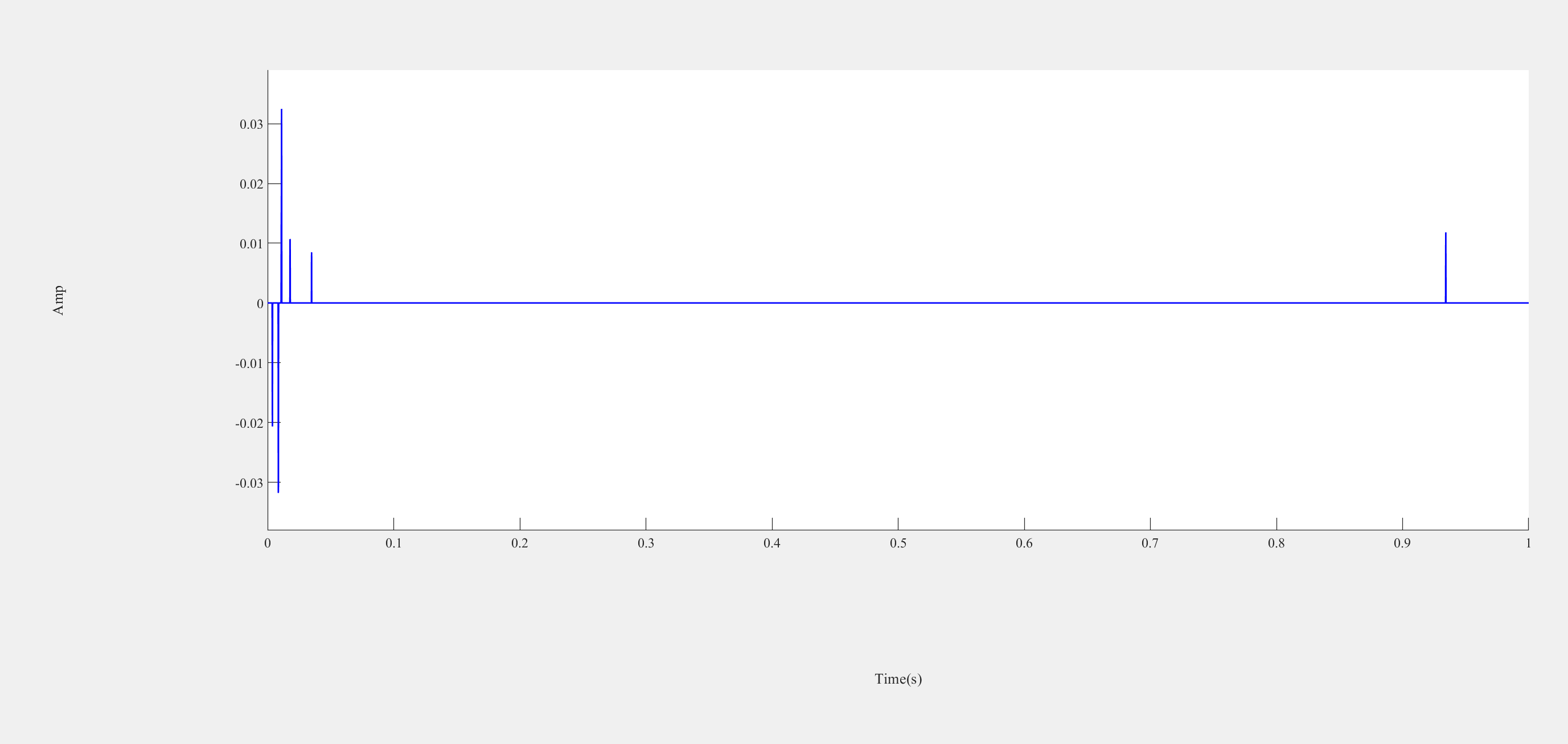
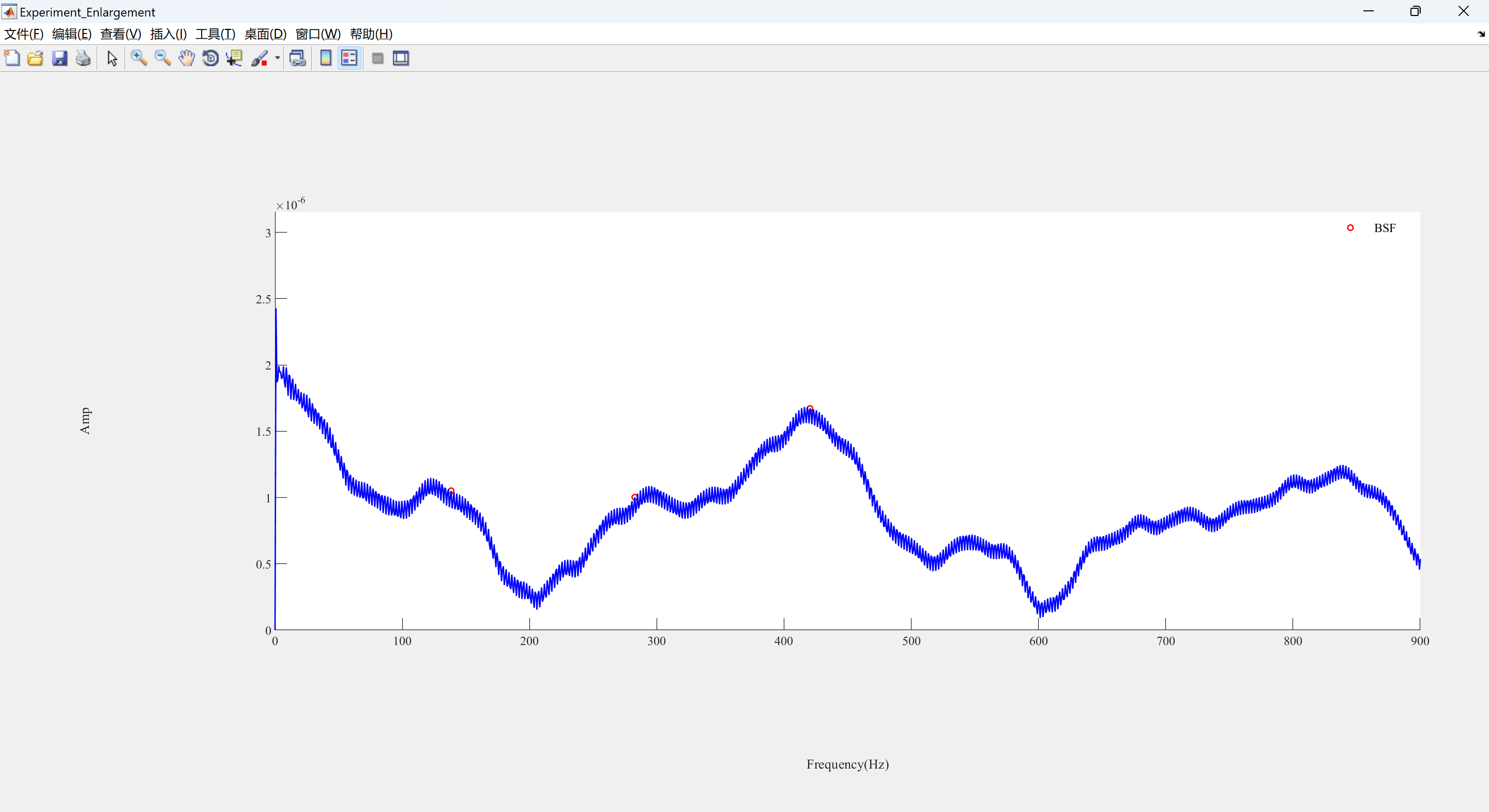
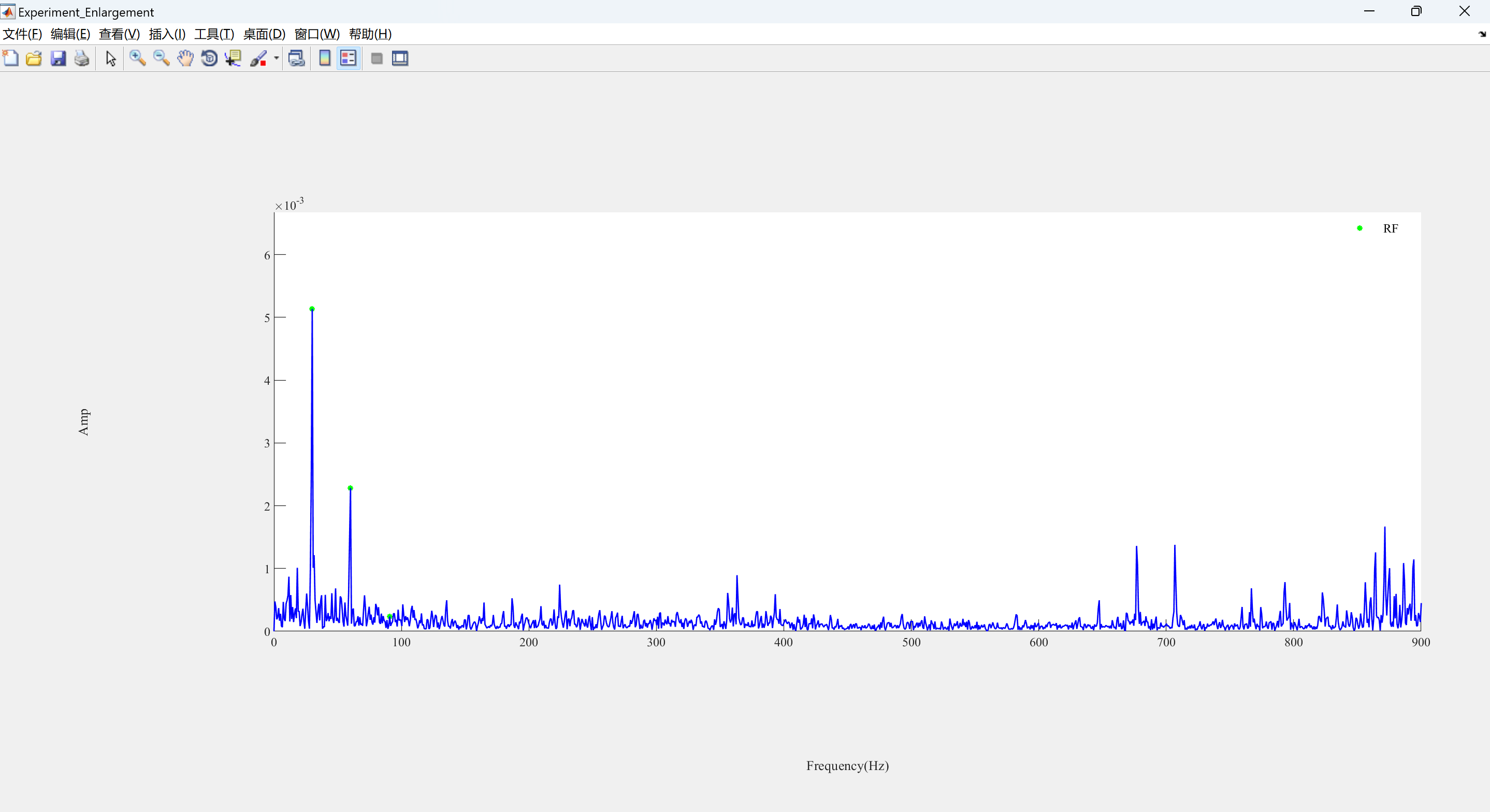
可视化部分代码:
%% Print the time domain
[WindowPosition,h1] = Subfigure11_cm(5, 1.5, 1.2, 0.3, 0.5, 0.9);
figure(1);clf;
set(gcf, 'NumberTitle','off','Name','Experiment_Time');
set(gcf, 'Units', 'centimeters');
set(gcf,'position',WindowPosition);
set(gcf, 'PaperPositionMode', 'auto');
h1_ap=axes('position',h1);
hold on
ph(1) = plot(t, x2, 'b-', 'LineWidth', LineWidth);
hold off
% box on
% legend1 = legend(ph, 'Noisy signal' , 'Noise-free signal');
% set(legend1,'location','best','Orientation','horizontal', 'FontSize',FontSize,'FontName',FontName)
% legend boxoff
%title(['FCER=', num2str(FCER_Nonconvex)],'FontSize',FontSize,'FontName',FontName);
xlim_min = min(t); xlim_max = max(t);
ylim_min = min(x2)*1.2; ylim_max = max(abs(x2))*1.2;
xylim = [xlim_min,xlim_max,ylim_min,ylim_max]; axis(xylim);
LabelX_Linchao(h1_ap,Tstring,xylim,x_side);
LabelY_Linchao(h1_ap,Astring,xylim,y_side);
set(h1_ap,'FontSize',FontSize,'FontName',FontName);
annotation('textbox',[0 1 0.03 0.03],'String',{'(a)'},'FontSize',FontSize+2,'FontName',FontName,'FontWeight','bold','FitBoxToText','off','LineStyle','none');
% save figure
SaveFigureLinchao('20a_CWRU_Experiment_SASD',FlagFigureAutoSave,currentFolder)
%% Print the freqeuncy domain
figure(2);clf;
set(gcf, 'NumberTitle','off','Name','Experiment_Enlargement');
set(gcf, 'Units', 'centimeters');
set(gcf,'position',WindowPosition);
set(gcf, 'PaperPositionMode', 'auto');
h1_ap=axes('position',h1);
hold on
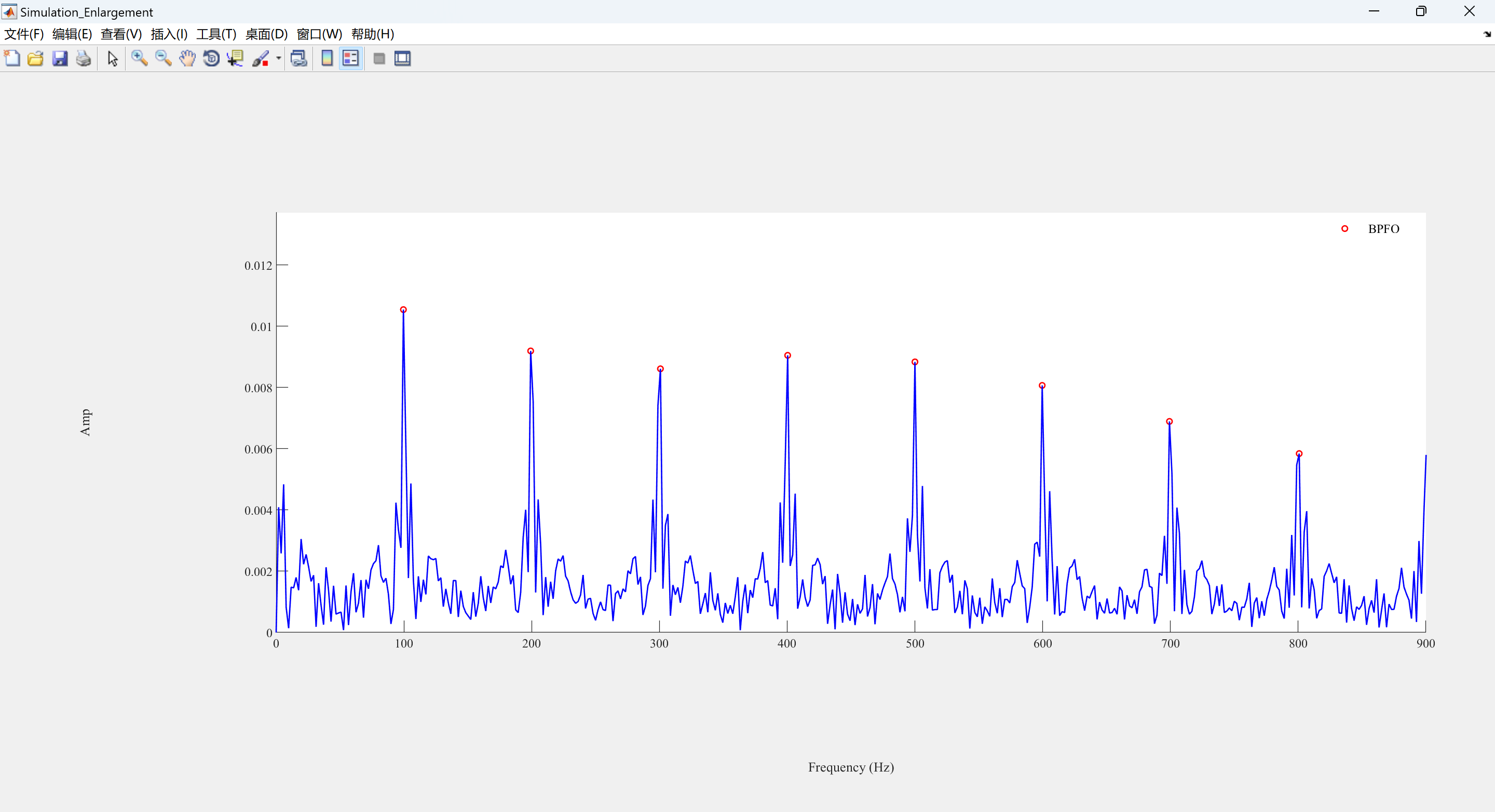
ph(1) = plot(Points_Index1, Points1, 'ro', 'LineWidth', LineWidth,'MarkerSize',MarkerSize);
ph(2) = plot(f2, yf2, 'b-', 'LineWidth', LineWidth);
hold off
legend1 = legend(ph, 'BSF');
set(legend1,'location', 'best', 'Orientation','horizontal', 'FontSize',FontSize,'FontName',FontName)
legend boxoff
xlim_min = 0; xlim_max = 900;
ylim_min = 0; ylim_max = max(abs(yf2))*1.3;%max(abs(yf1))*1.3;
xylim = [xlim_min,xlim_max,ylim_min,ylim_max]; axis(xylim);
LabelX_Linchao(h1_ap,Fstring,xylim,x_side);
LabelY_Linchao(h1_ap,Astring,xylim,y_side);
set(h1_ap,'FontSize',FontSize,'FontName',FontName);
annotation('textbox',[0 1 0.03 0.03],'String',{'(b)'},'FontSize',FontSize+2,'FontName',FontName,'FontWeight','bold','FitBoxToText','off','LineStyle','none');
% save figure
SaveFigureLinchao('20b_CWRU_Experiment_Enlargement',FlagFigureAutoSave,currentFolder)
%% Print the time domain
figure(3);clf;
set(gcf, 'NumberTitle','off','Name','Experiment_Time');
set(gcf, 'Units', 'centimeters');
set(gcf,'position',WindowPosition);
set(gcf, 'PaperPositionMode', 'auto');
h1_ap=axes('position',h1);
hold on
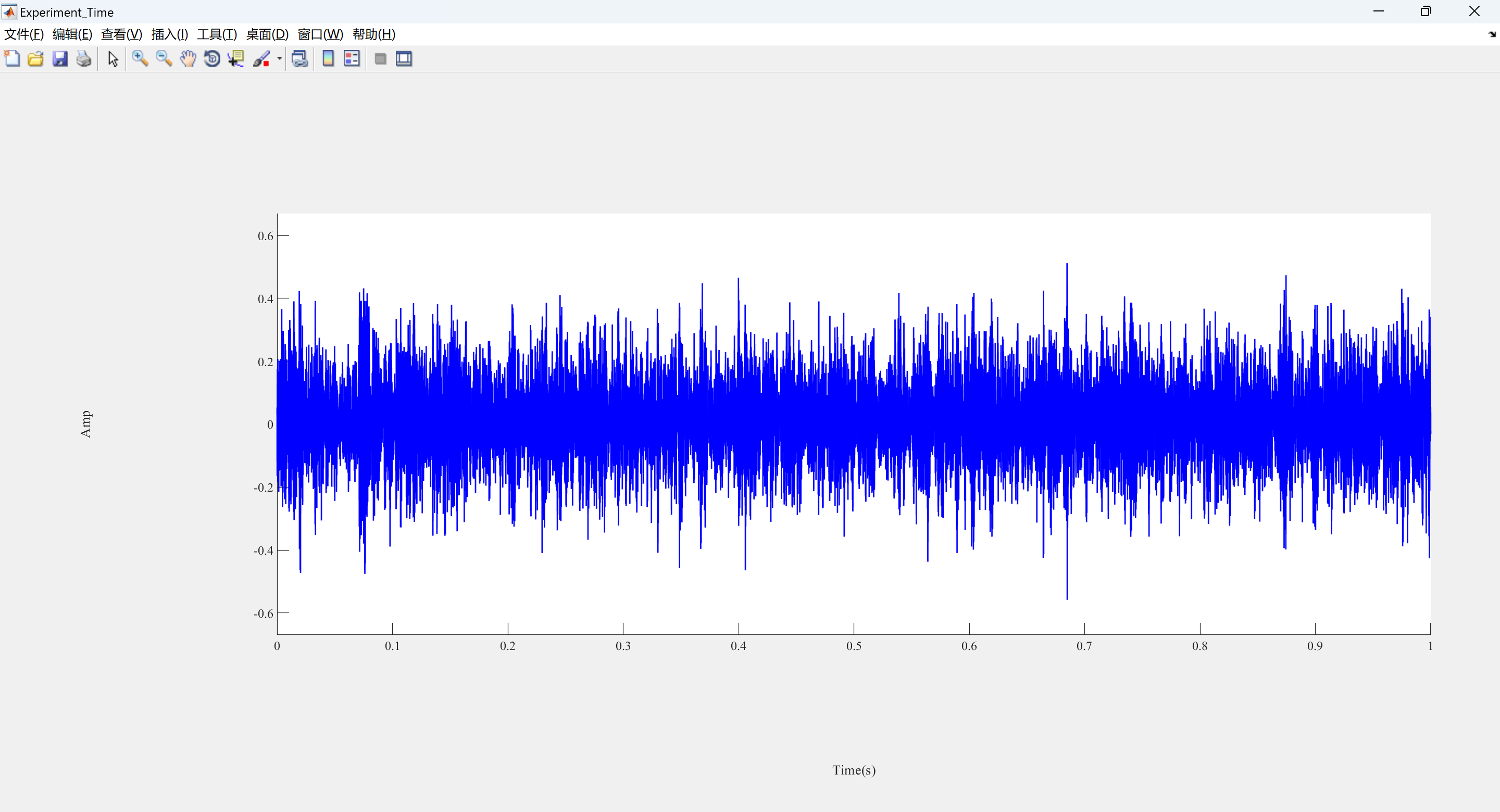
ph(1) = plot(t, x1, 'b-', 'LineWidth', LineWidth);
hold off
% box on
% legend1 = legend(ph, 'Noisy signal' , 'Noise-free signal');
% set(legend1,'location','best','Orientation','horizontal', 'FontSize',FontSize,'FontName',FontName)
% legend boxoff
% title(['RMSE=', num2str(RMSE_Harmonic)],'FontSize',FontSize,'FontName',FontName);
xlim_min = min(t); xlim_max = max(t);
ylim_min = -max(abs(x1))*1.2; ylim_max = max(abs(x1))*1.2;
xylim = [xlim_min,xlim_max,ylim_min,ylim_max]; axis(xylim);
LabelX_Linchao(h1_ap,Tstring,xylim,x_side);
LabelY_Linchao(h1_ap,Astring,xylim,y_side);
set(h1_ap,'FontSize',FontSize,'FontName',FontName);
annotation('textbox',[0 1 0.03 0.03],'String',{'(c)'},'FontSize',FontSize+2,'FontName',FontName,'FontWeight','bold','FitBoxToText','off','LineStyle','none');
% save figure
SaveFigureLinchao('20c_CWRU_Experiment_SASD',FlagFigureAutoSave,currentFolder)
%% Print the freqeuncy domain
figure(4);clf;
set(gcf, 'NumberTitle','off','Name','Experiment_Enlargement');
set(gcf, 'Units', 'centimeters');
set(gcf,'position',WindowPosition);
set(gcf, 'PaperPositionMode', 'auto');
h1_ap=axes('position',h1);
hold on
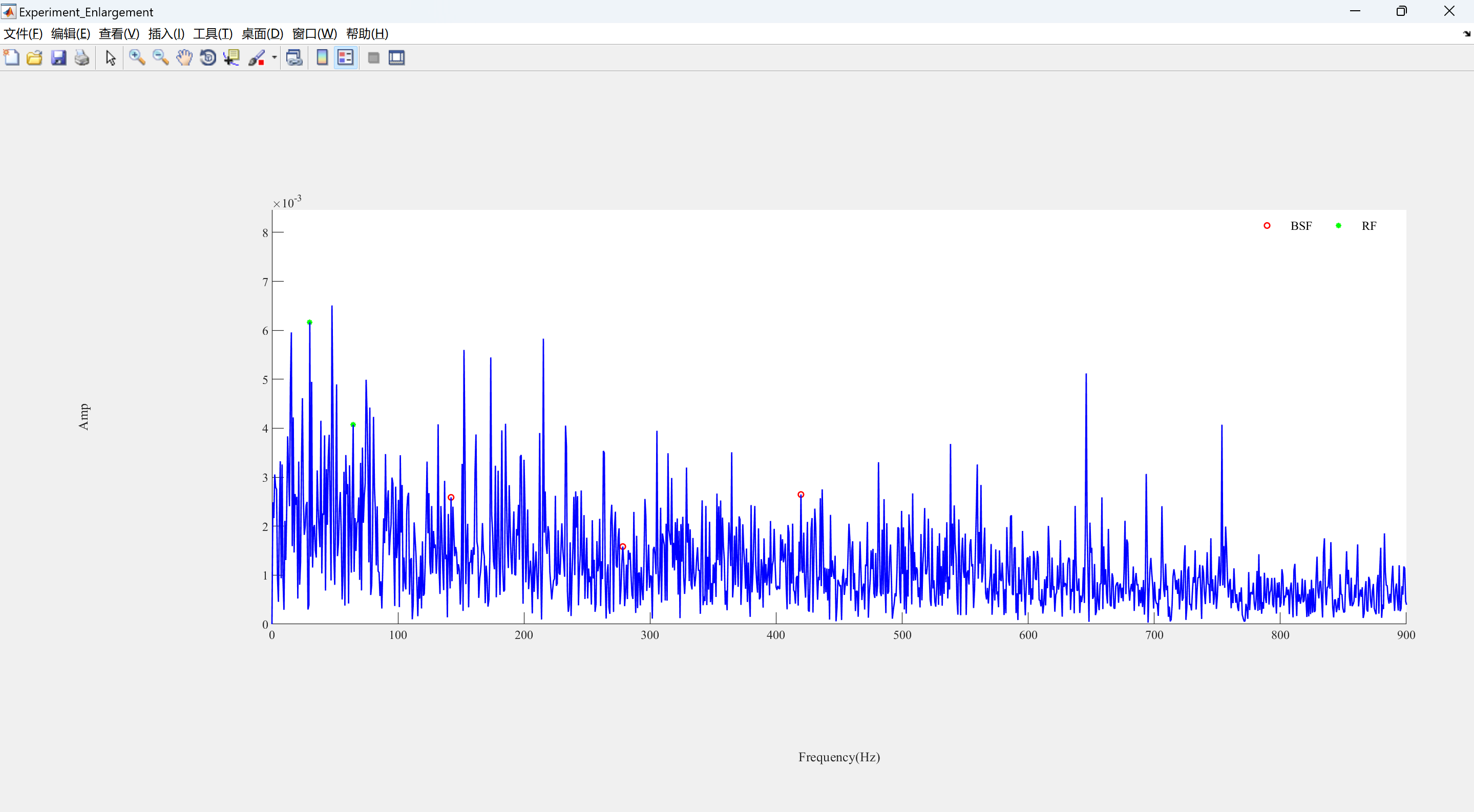
ph(1) = plot(Points_Index2, Points2, 'g*', 'LineWidth', LineWidth,'MarkerSize',MarkerSize);
ph(2) = plot(f1, yf1, 'b-', 'LineWidth', LineWidth);
hold off
legend1 = legend(ph, 'RF');
set(legend1,'location', 'best', 'Orientation','horizontal', 'FontSize',FontSize,'FontName',FontName)
legend boxoff
xlim_min = 0; xlim_max = 900;
ylim_min = 0; ylim_max = max(abs(yf1))*1.3;%max(abs(yf1))*1.3;
xylim = [xlim_min,xlim_max,ylim_min,ylim_max]; axis(xylim);
LabelX_Linchao(h1_ap,Fstring,xylim,x_side);
LabelY_Linchao(h1_ap,Astring,xylim,y_side);
set(h1_ap,'FontSize',FontSize,'FontName',FontName);
annotation('textbox',[0 1 0.03 0.03],'String',{'(d)'},'FontSize',FontSize+2,'FontName',FontName,'FontWeight','bold','FitBoxToText','off','LineStyle','none');
% save figure
SaveFigureLinchao('20d_CWRU_Experiment_Enlargement',FlagFigureAutoSave,currentFolder)
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。





















 898
898

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








