基于体素化的游戏寻路导航网格自动生成算法

前言

在两年前我发布了两篇文章：
多边形分割成若干凸多边形（NavMesh的初步形成）
在Unity中实现体素化
当时我正开始做毕设，因为从小对游戏感兴趣，所以找老师开了这么一个题目，不过后来因为事情繁忙（偷懒太久），文章一直没有更新，到如今我都从清纯校招生变成工作一年半的老油条了。

最近整理了一下当时的资料，开源了项目代码，并且将毕设论文中的“干货”部分，发表出来。一方面希望能够给对这个方面感兴趣的同学一点学习的参考，另一方面，如果我的内容存在错误，也希望能够被指出，我也能在不断改正的过程中成长。

开源地址：Github:Navigation
本文的余下部分则由我从我的毕业论文中节选出来的一部分内容稍作调整组成。

工具框架设计

吐槽一下，这部分内容主要是毕设论文格式要求一定要有的，因为不少人的毕设是那种大的 Java 项目，前后端的，微服务啥的，所以价格图能整的挺复杂的，我这个就显得很简单。这部分我感觉我写的不太好的，参考意义可能并不是很大（更别提还有不少内容写出来是为了增加字数撑场面的 2333）
> 关注算法设计的同学可以直接跳转本文的 “算法设计” 章节观看！

作为Unity package，本工具会涉及到与Unity引擎以及游戏交互，具体的架构如下图所示。本工具在图中用“Navigation Toolset”表示，其Editor部分内嵌在Unity引擎中，使得游戏开发人员可以方便地配置各项用于生成导航网格的参数。而导航网格的生成逻辑以及寻路和避障算法则是独立于引擎的模块，这也使得本工具能够方便地移植到其他游戏引擎中。

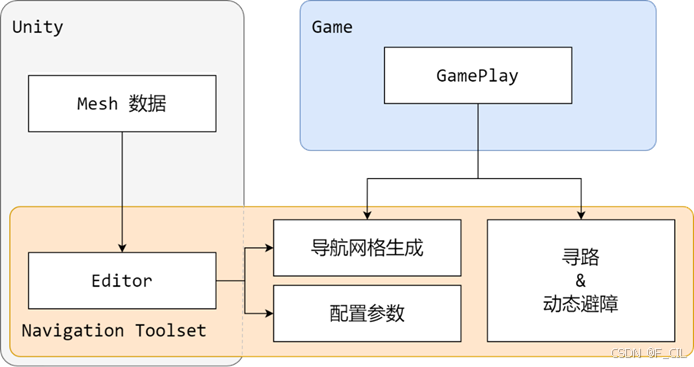
由于在Unity下的开发，Unity会自动识别“Editor”文件夹，并在打包时将其剔除，因此基于Unity的开发一般会在顶层分为三个模块：Editor、Runtime和Shared。Editor和Runtime下的模块会依赖Shared下的模块，但Editor和Runtime是完全解耦的。

Editor模块是用来在Unity编辑器中扩展功能和界面的，比如自定义Inspector、Window、Menu等。editor模块中的代码只会在Unity编辑器中执行，不会被打包到最终的游戏中。

Runtime模块是用来在游戏运行时提供功能和逻辑的，比如游戏场景和角色的数据、各个模块（如寻路模块、渲染模块）的代码、美术资源、音效等。Runtime模块中的代码会被打包到最终的游戏中，并且可以根据不同的平台进行优化和适配。

Shared模块是用来在Editor和Runtime之间共享数据和代码的，比如定义一些常量、枚举、结构体、接口等。Shared模块中的代码既可以在Unity编辑器中使用，也可以在游戏运行时使用。

这样分模块的好处是可以提高代码的可读性、可维护性和可复用性，也可以避免一些不必要的编译错误和运行时错误。本工具软件在每个层次下的功能模块设计如下图所示。

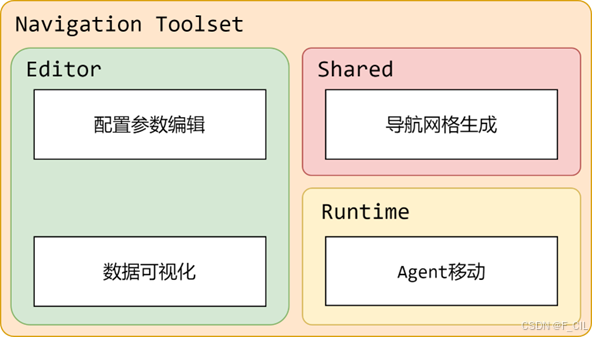
1. 配置参数编辑
编辑配置参数是开发人员最频繁接触的模块，配置参数包含Agent数据、Area数据、导航网格生成设置以及场景物体的Static Obstacle组件数据。该模块使用IMGUI完成编辑器UI的开发，开发人员可以方便地在编辑器UI中编辑各项配置参数。

2. 数据可视化
在完成NavMesh的生成后，开发人员通常需要查看一下NavMesh的具体形态。这部分的功能为绘制NavMesh数据和测试寻路功能两部分。其中，NavMesh数据包含体素、行走面、距离场、区域划分、原始轮廓线、简化轮廓线、凸多边形网格、高度细节和NavMesh九种。开发人员可以任意选择和切换要绘制的内容。测试寻路功能即开发人员可以在场景中任意指定起点和终点，本工具会计算出从起点到终点的最短路径并绘制在场景中（注意此时并非调用A*寻路模块）。

3. 导航网格生成
NavMesh生成模块包含了NavMesh生成的全部流程。当开发人员完成配置参数编辑后，便可启动该模块用于导航网格生成。同时，在游戏运行过程中，使用信号机制，当Static Obstacle发生变化时，发出信号通知该模块实时更新场景的导航网格。

4. Agent移动
该模块提供了寻路和避障功能，使得Agent可以在游戏场景中自由的移动。开发人员仅需为Agent挂载Navigation Agent组件，并在Agent需要移动时，将Navigation Agent组件的Destination属性赋值为目的地坐标，该模块便会自动调用A*算法为Agent规划路径，并在Agent移动过程中使用ORCA动态避障算法为其提供实时避障支持。

相关数据结构设计

配置参数设计

配置参数包含了导航网格生成所依赖的配置项，主要包括寻路智能体（Agent）、寻路区域（Area）和导航网格生成偏好三部分，其UML类图如下所示。图中，NavMeshPreference表示主要配置参数集合，Agents为寻路智能体集合，Areas为寻路区域集合，BuildInfo为导航网格生成偏好。
除此之外，Logger设置和输出数据设置也属于配置参数的一部分。为了便于读取和保存配置参数，本文利用Unity提供的Scriptable Object格式存储各类配置参数。

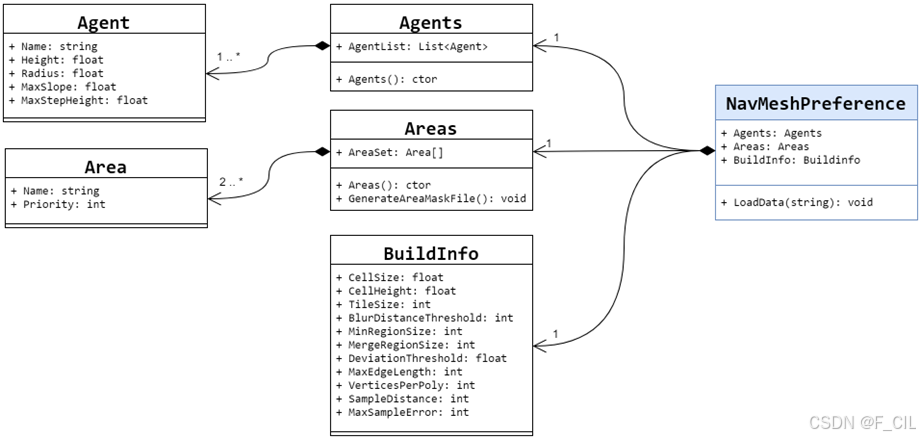
寻路智能体（Agent）
在游戏寻路中，为了简化计算，通常使用胶囊体（Capsule）来抽象表示人形的单位。此时，Height和Radius也即是该胶囊体的高度和半径。

游戏中Agent最基础的移动能力为爬坡和上台阶，例如Max Slope = 45°Max Step Height = 0.6，则该Agent只能在倾角小于等于45°的面上移动，并且最高能上0.6m的台阶。

对于一个Height = 2，Radius = 0.2，Max Step Height = 1.2，Max Slope = 45°的Agent来说，其样式类似下图所示。其中，红色方框框出了Agent的大致尺寸，蓝色高为1.2的台阶表示了该Agent最高能攀登的台阶高度，绿色倾角为45°的斜线表示了该Agent能移动的最陡峭的面。

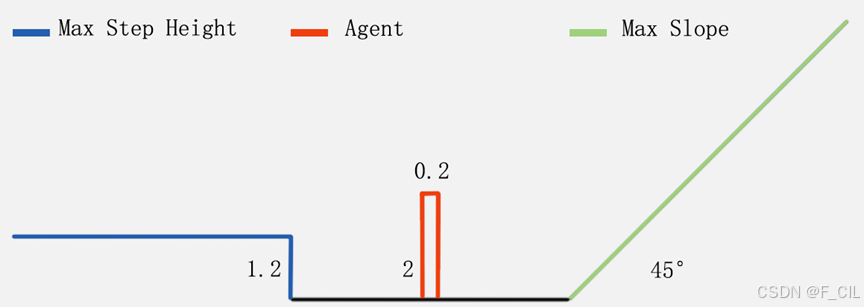
Agents为一个Scriptable Object，其中包含一个Agent类型的列表。维护了全部已有的Agent。在生成导航网格时会读取Agents中的列表，并为每个Agent生成一份导航网格。

同时在本工具实现了一个代码生成器，当开发人员编辑完Agent后，会自动根据当前已有的Agent，生成一个枚举类型，以Agent的名称作为枚举项。这样，可以方便开发人员在代码中为不同的Agent实现一些定制化的功能。

寻路区域（Areas）

在游戏中，往往存在着多种多样的地表类型，例如公路、草地、雪地、冰面、沙漠等。Agent在不同类型的表面上移动的代价往往也不同，例如在公路移动时消耗一倍的体力，而在沙漠移动同样的距离要消耗两倍的体力。故而本工具支持为不同的表面类型赋予不同的优先级，从而影响寻路的结果。例如将公路的优先级设为1，沙漠的优先级设为2，那么只有当走公路距离超过走沙漠距离的两倍时，Agent才会选择走沙漠。

Areas为一个Scriptable Object，其中包含一个Area类型的列表。维护了全部已有的Area。在开发人员编辑完Area后，同样会使用代码生成器为Areas生成一个枚举类型，以Area的名称作为枚举项。这也使得开发人员能够很方便的在代码中访问所有已定义的表面类型。

这里补充一下，最后因为时间紧急，分不同区域实现不同的寻路代价这里其实没做出来 QwQ

导航网格生成偏好（BuildInfo）

该部分为导航网格生成流水线的详细配置项，通过修改这些配置项，可以控制导航网格的生成速度、精细度。

Cell Size和Cell Height用来控制体素的尺寸，由于大部分游戏在平面上对精度的需求比较高，而在立体空间中通常不需要特别高的精度（能区分上下表面即可），故而我们可以将Cell Size设置的较小而略微调大一些Cell Height，这样可以在能够实现需求的基础上以更快的速度生成导航网格。

Tile Size用来切分场景，由于体素化环节存储体素需要占用过大的内存，这使得我们无法一次性为一个巨大的场景完整的生成导航网格，而需要将其依据Tile Size分成若干块，先对每个小块生成导航网格，在为每个Tile边缘的网格建立起和相邻Tile边缘的导航网格的连接关系。同时在游戏运行时，如果场景中新增了一些障碍物，也无需重新生成整个场景的导航网格，而是仅需要重新生成障碍物所在的Tile的导航网格。

Blur Distance Threshold用于模糊距离场数据，对于距离场中大于该参数的值才进行模糊化操作，这继而会影响区域划分的效果。

Min Region Size和Merge Region Size是用来对区域划分结果进行二次过滤。对于一个不予其他区域连通的Region，如果他的尺寸（包含的Span数量）小于Min Region Size，我们就认为这个Region没有参考价值，将其抛弃掉。对于一个和其他区域连通的Region，如果他的尺寸小于Merge Region Size，那么我们就将其合并到与他相邻的区域中，这样可以避免产生很多细小的区域。

Deviation Threshold用于在简化轮廓线时决定是否还需要继续迭代。当Raw Contour中所有点距离Simplified Contour的距离均小于Deviation Threshold时，说明此时Simplified Contour的精度已经满足要求，否则需要将偏差最大的点添加进Simplified Contour中，继续迭代。

Max Edge Length用于二次处理Simplified Contour，将其中长度大于该参数的边分割成长度小于等于Max Edge Length的多段。做该项处理的目的是为了避免部分边过长而导致在后续流程中生成一些特别狭长的三角面。

Vertices Per Poly用于处理PolyMesh Field，在耳切法将Simplified Contour切割成若干三角面后，在合成过程中当两个多边形的点数和大于了Vertices Per Poly，则说明这两个多边形不能合并。做该项处理的目的是为了避免在合并三角面后得到的多边形均衡性较差的问题。均衡性较差指的出现部分多边形点数特别多的情况，我们希望合并三角面后所得的多边形点数尽量相近。

Sample Distance和Max Sample Error用于补充高度细节环节。其中不论是边采样还是面采样，采样点的距离间隔都是Sample Distance，并且采样点偏差大于Max Sample Error则说明该采样点应当被选中，并继续迭代。如果所有采样点偏差都低于Sample Distance，则可以结束采样。

BuildInfo使用两个Scriptable Object存储，其中一个存储每个参数的默认值，另一个存储用户当前的设定值。

Logger设置与输出数据设置

这两部分配置参数不会被导航网格生成模块直接使用，故而没有被放到NavMeshPreference集合中，而是被统一放在SettingData中。

LogLevel为枚举类型，共有5个等级：Debug、Info、Warning、Error、Fatal。设置Level后，Logger仅会输出等级不低于Level的日志内容。
其余属性均为布尔类型，为True说明开启该项功能，为False说明关闭该项功能。需要注意的是，Save NavMesh Data选项在UI界面中被强制绑定为True，因为其余三项数据属于导航网格生成中间数据，可以不保存，而NavMesh数据为导航网格生成的最终数据，必须保存才能使用。

导航网格数据设计

导航网格生成所需的数据存储在Pipeline Data中，主要包含五类数据：Solid Height Field、Compact Height Field、Contour Set、Poly Mesh Field和Triangle Mesh，其中Solid Height Field存储体素化生成的实心高度场；Compact Height Field存储生成的紧缩高度场；Contour Set存储了轮廓线数据，包含了原始轮廓线和简化轮廓线；Poly Mesh Field存储了凸多边形网格数据；Triangle Mesh存储了三角形网格数据。

五类数据与导航网格生成的六大环节对应，后面的数据往往依赖前面的数据，例如Solid Height Field数据是在体素构建环节中生成的；Compact Height Field数据是在行走面过滤环节中，依赖Solid Height Field而初步生成，在区域划分环节中为其中的每个Span计算了其所属于的区域；Contour Set数据是在构建轮廓线环节，根据Compact Height Field中每个Span的区域生成的；Poly Mesh Field数据是在构建凸多边形环节中，根据Contour Set中的轮廓线数据生成的；Triangle Mesh数据是在补充高度细节时，根据Compact Height Field和Poly Mesh Field生成的。

在体素化时，由于不可预估场景需要用多少Solid Span描述，故而使用字典记录每个平面坐标上的第一个Span，并用链表链接起上方的所有Span。这样存储可以减少内存占用，但是数据离散在内存中，不利于提高访问速度。

在反体素化生成Compact Height Field时，由于已知场景中Solid Span的数量，故而可以直接使用数组维护所有生成的Compact Span，此时每个Span拥有一个唯一的数组下标。同样，也通过记录数组下标的方式，记录其上方的Span以及其四周的邻居Span。这样存储使得在遍历Compact Height Field时获得更高的cache命中率，从而极大的提高运行速度。

在后续步骤中，记录多边形也同样使用数组的方式，与传统的OOP（Object-oriented programming）相比，可以在使用更少的存储空间的同时，获取更高的访问速度。

在RawVertices中，从下标0开始，使用连续的四个数表示一个顶点的（x，y，z）坐标和所属的区域（为了减少顶点总数，相邻的区域会共享一部分顶点，所以会出现Contour顶点所属的区域与Contour所属的区域不同的情况）。在SimplifiedVertices中，由于全部简化顶点均来自于原始顶点，所以仅需记录顶点在RawVertices中的下标即可。如下图所示，上方为RawVertices，不同颜色表示不同的顶点，下方为SimplifiedVertices，由于化简后仅需使用原始顶点中的第0，1，5，6个顶点，故而仅需在SimplifiedVertices中存储0，1，5，6四个数。

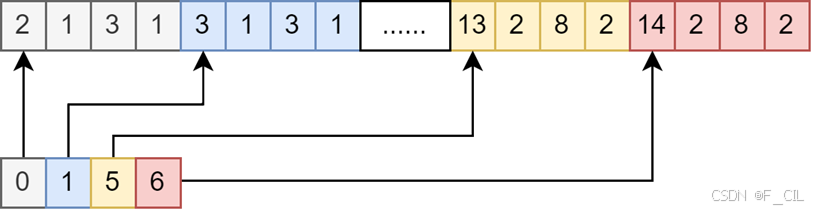
在 PolyMesh Field 数据中，同样由于相邻的凸多边形会共享一部分顶点，所以使用Vertices数组存储将全部顶点。每个凸多边形只需记录它们包含的顶点在Vertices数组中的下标即可。

在BuildInfo中，使用Vertices Per Poly属性限制了每个凸多边形的顶点数，所以可以为每个凸多边形申请大小为Vertices Per Poly的空间用于记录自己的顶点在Vertices数组中的下标。具体的Polygons数组与Vertices数组的对应关系下图所示：图中上方为Vertices数组，不同颜色表示不同的顶点，下方为Polygons数组，此时Vertices Per Poly为3，故而每三位代表一个凸多边形。

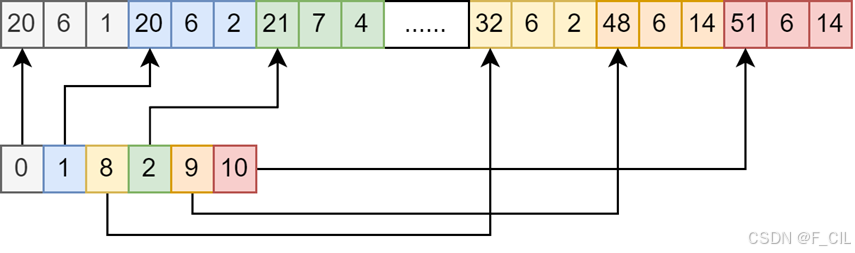
Triangle Mesh数据具体结构设计与PolyMesh Field在Vertices Per Poly = 3时类似。不过在PolyMesh Field中，仍使用体素坐标作为顶点坐标，而在Triangle Mesh中，由于要贴合实际障碍物表面，故而使用实际的世界坐标作为顶点坐标，需要使用浮点数存储。

导航网格数据结构部分的UML类图如下图所示。

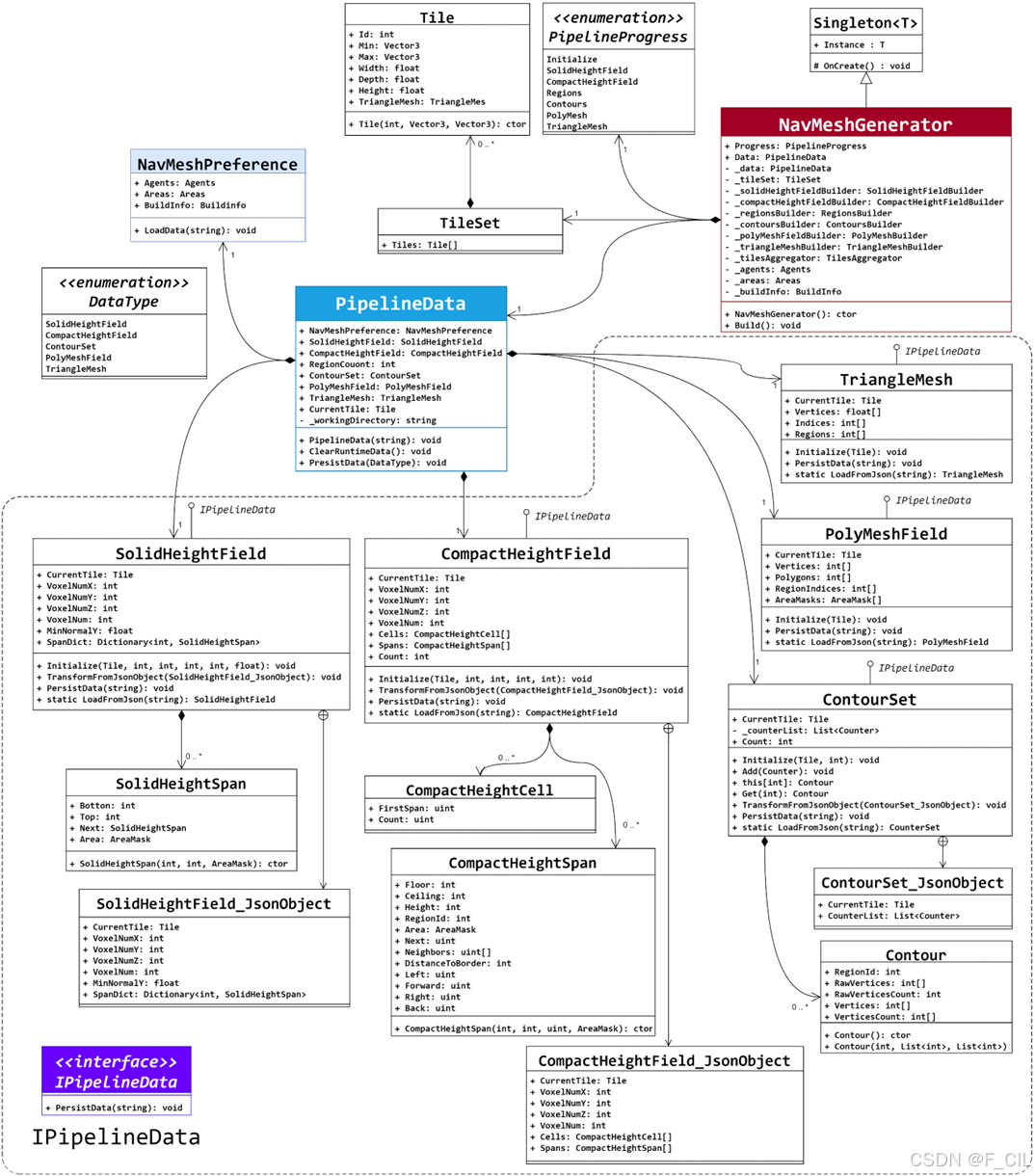
组件设计

在Unity中，通常使用组件模式为物体添加各项功能。故而在本文中，制作了Static Obstacle和Navigation Agent两个组件，分别实现将物体标记为障碍物和为物体提供移动能力的功能。

补充一下，这部分也是看看就好，当时因为时间紧张，导航网格只能离线生成，并没有真正实现运行时动态更新 QwQ

Static Obstacle组件
Static Obstacle组件，通过OnActive和OnInactive两个事件，可以在自身状态发生变化时，通知导航网格生成模块，进行导航网格的动态修改。同时在导航网格的静态生成环节中，仅会处理挂载了本组件的物体。

Navigation Agent组件
Navigation Agent组件中，Speed、Rotation Speed与Acceleration是Agent移动的基本参数；Stopping Distance和Auto Breaking 在Agent接近目标点时起作用，用于微调Agent的移动表现；Quality Level和Priority用于控制Agent的避障表现，其中Quality Level共有Low、Medium、High三级，低级别的避障质量会有更高的效率，高级别的避障质量有精确的避障表现，Priority值越小的单位，在避障环节拥有更高的优先级，越高优先级的Agent在避障时对自身速度方向的修改会越小；Walkable Area用于记录该Agent可以移动的区域，从而在寻路时避开不包含在Walkable Area中的区域；开启Auto Repath功能，当Agent在移动过程中，如果地图发生变化导致本可以通行的路被阻塞，会自动重新寻路，否则Agent将会移动到阻塞的障碍物附近就停止移动。

算法设计

基于体素的导航网格生成算法

体素构建

体素（Voxel）是体积元素（Volume Pixel）的简称，可以被理解为像素在三维空间中的形态。将一个简单的游戏场景体素化处理后的效果如下图所示，每个红色的方框代表一个体素。

空间中一个不规则的多边形面片所占用体素的效果如下图所示，每个黑色的方框代表一个体素。

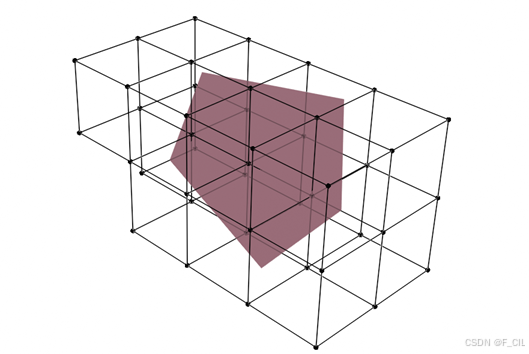
在体素构建环节，使用实心高度场（Solid Height Field）存储体素数据。将连续的体素使用区间（Solid Span）去描述。如下图所示，连续的体素用一个Span存储，红线表示Span的Next指向，这里为了避免红线过多，仅展示了部分Span的Next。

Bounds：包围盒，即AABB（Axis aligned bounding box）盒，是可将三角面T完全包围的尺寸最小的长方体。一个包围盒通常只需要两个顶点Min和Max定义，其计算方法如下。

三角面Bounds计算方法
输入：三角面
输出：Bounds
	1. 枚举三角面的三个顶点，Min顶点的x、y、z三个分量均取三个顶点中对应分量的最小值；
	2. 枚举三角面的三个顶点，Max顶点的x、y、z三个分量均取三个顶点中对应分量的最大值；
	3. 结束。

在2维平面中（X轴与Z轴组成的平面，即XOZ平面），体素化也即网格化步骤如下所示，这一步操作在计算机图形学中通常被称作“光栅化”。

二维平面下的体素化
输入：三角面
输出：体素数据
	1. 求出三角面的Bounds，计算其覆盖体素在z方向的取值范围；
	2. 逐个枚举z，将三角形分为上、下两部分，取下部分进行3操作；枚举结束则去5；
	3. 对于2中下部分，求出其覆盖的体素在x方向的取值范围；
	4. 逐个枚举x，标记左侧部分所占用的体素，返回2；
	5. 结束。

上述算法中第1~2步的效果如下图所示，左侧用红色的线标记出第2步每个枚举到的z，将三角面分割成了右侧若干用绿色框框出的多边形面。

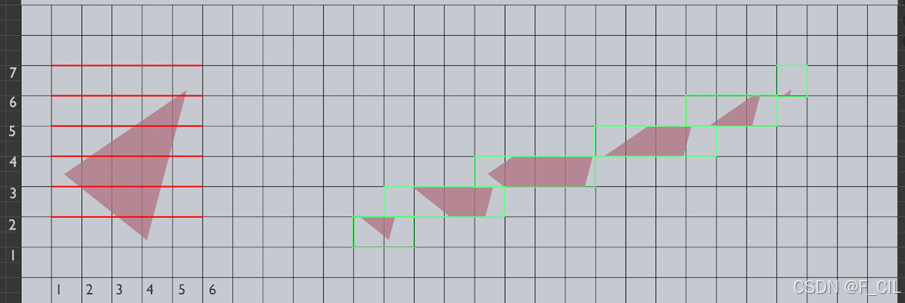
第3~4步的效果如图3-12所示，左侧用淡蓝色框出的为该三角面占用的体素，右侧用红色线标记出了第4步每个枚举到的x。

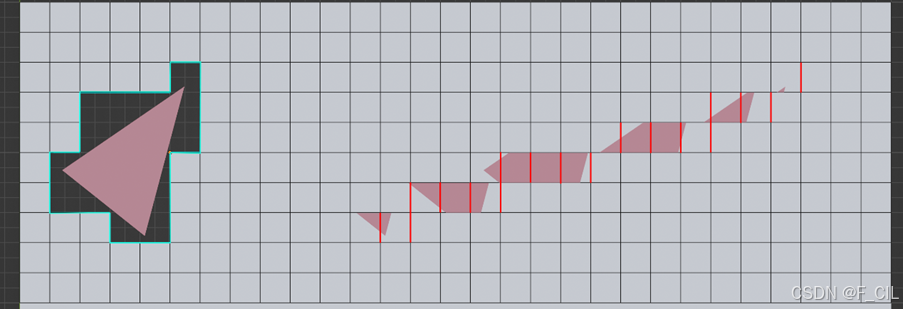
三维空间的体素化算法是在二维算法的基础上做的延伸，具体步骤下。

三维空间下的体素化
输入：三角面
输出：体素数据
	1. 求出三角面在XOZ平面上的投影面F；
	2. 计算F的Bounds，求其覆盖体素在z方向的取值范围；
	3. 逐个枚举z，将三角形分为上、下两部分，取下部分进行4操作，枚举结束则去7；
	4. 对于3中下部分，求出其覆盖的体素在x方向的取值范围；
	5. 逐个枚举x，求其左侧部分在y轴上的取值范围，枚举结束则返回3；
	6. 逐个枚举y，标记占用的体素，返回5；
	7. 结束。

完成体素构建后，游戏场景被抽象成大量Solid Span存储在Solid Height Field中。此时需要添加几个过滤步骤，提供一些容错并且初步剔除一些不合理的区域。
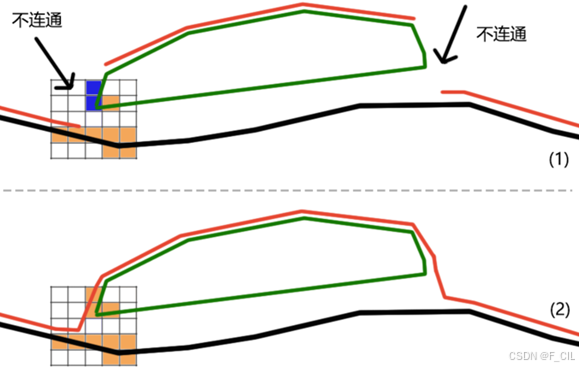
首先是过滤悬空的障碍物，如下图所示，黑线表示地面，绿色表示一个放置在地面上的物体。一般来说在往游戏场景中放置物体时，会将其嵌进地形中（如图(2)），但通常由于地形并不平整，在放置一些物体时，可能会出现并没有将物体完全嵌在地形中，而是有一些边缘漏了出来（如图(1)）。图中用橙色表示仅考虑Max Slope，Agent可以站立的体素。蓝色表示由于坡度过大Agent无法站立的体素。可以发现由于往游戏场景中摆放物体出现的一些精度问题，会导致一些我们希望Agent可以走的区域变得无法行走。所以我们需要检测现有的不可行走的Span，如果它下方的Span可行走，并且它与下方的距离小于Max Step Height，我们就认为这是由于摆放物体时出现误差导致的，将其重新设置成可行走的。

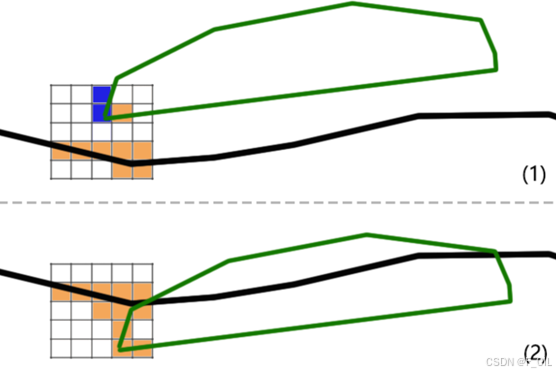
添加此项过滤的效果如下图所示，用红色的线表示使用该Solid Span数据得到的行走面。不难看出，添加此项过滤后，可以得到整个连通的行走面，否则Agent将无法从左侧移动到右侧。

其次是过滤“孤岛”障碍物。有时游戏中小物体数量过于多时，手动去甄别哪些需要用于生成导航网格，并为其添加Static Obstacle组件，工作量大且操作非常繁琐。此时开发人员可能会一次性直接为绝大部分物体挂载Static Obstacle组件，这使得生成的Solid Span可能有很多“孤岛”，即在四个方向上均没有其他Solid Span与之相邻。这种情况我们认为是一些非常小的物件导致的，这类小物件在生成导航网格时通常无需考虑。这一步过滤使得即便一次性为复杂场景中全部物体添加Static Obstacle组件，仍能得到比较理想的导航网格。

最后是过滤高度空间不足Solid Span。即便一个Span是可以行走的，但是由于它距离它上方的Span的距离小于Agent的高度，使得这个区域无法放置一个Agent，所以要将它修改为不可行走。

行走面过滤

在体素构建过程中，我们使用Solid Height Field存储了障碍物所占用的体素数据。在这一节，将对Solid Height Field进行反体素化得到紧缩高度场（Compact Height Field），从而获得游戏单位（亦称Agent）实际可以移动的范围。
Compact Height Field存储体素的效果如下图所示。

1. 反体素化
反体素化也就是对Solid Height Field取补集的过程，过程如下所示。

反体素化流程
输入：Solid Height Field
输出：Compact Height Field
	1. 在XOZ平面上枚举每个体素区域的第一个Solid Span A，枚举结束则去4；
	2. 若A的Next不为空，则将A的Top到A的Next的Bottom这块区域构建成一个Span，并沿着Next方向反复执行2，否则去3；
	3. 将A的Top到 + ∞ 这块区域构建成一个Span，返回1；
	4. 结束。

2. 建立连接关系
为了描述Agent可以移动的区域，需要将每个Compact Span和他的前后左右四个邻居连接起来，从而在后续步骤中逐渐转换成多边形面。
为Compact Span建立连接关系的方法如下所示。

建立Compact Span的连接关系
输入：Compact Height Field
输出：包含连接关系的Compact Height Field
	1. 在XOZ平面上枚举每个体素区域的全部Span，枚举结束则去3；
	2. 在4方向相邻体素区域中找到高度和Span最接近且符合Agent移动能力的第一个Span，并建立这两个Span的连接关系，返回1；
	3. 结束。

建立连接关系的Span状态示意如下图所示。需要注意的是，图中为了明显地画出连接的线，故而相邻Span之间有较大的间隔，实际上它们是紧密相邻的。

3.4.1.3区域划分
通过前两步，将物体原始三角面映射到了体素空间中，后续的操作仅需要使用体素数据去完成。这使得不论多复杂的场景，所处理的数据都是有限的体素。
我们通过勾画出Compact Height Field的轮廓，将其转换成若干多边形，再进行凸多边形化等操作得到凸多边形网格。然而，现在的Compact Height Field可能存在覆盖面过大，形态过于复杂等问题，使得后续的操作不能取得最好的效果。所以，需要划分现有的Compact Height Field成若干尺寸适当，形态简单的区域。

形态简单： 指的是区域内体素的高差在一定的范围内，并且不存在上下覆盖关系。

上图为使用蓝、绿、紫三个颜色分别描述了三个符合形态简单标准的区域，而下图所示则是用红色描述了一个不符合标准的区域。因为在这个区域中，存在一部分体素上方仍有同一区域内的其他体素，这会使得后续操作的效果变差。

进行区域划分存在多种算法，本文将使用经典算法，即分水岭（Watershed）算法，来实现该功能。
分水岭算法是一种常用于图像分割处理的算法，基于灰度图运行。在这里，使用距离场（Distance Field）来运行分水岭算法。
距离指的是每个体素距离边缘（不可行走区域）的距离，距离场即是所有体素距离的集合，如下图所示。图中，颜色越红表示距离边缘越远。

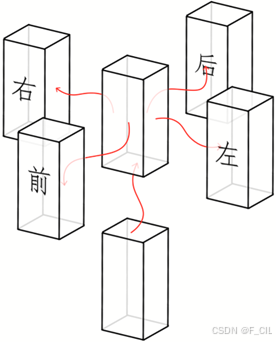
本文在计算距离场时将使用Saito算法。该算法分为两部分，先从左下角向右上角扫描，再反方向扫描，从而计算得到每个体素到达边缘的距离。其中，方向的定义与坐标的关系如下图所示。

Saito算法的描述如下所示。

Saito算法
输入：Compact Height Field
输出：Distance Field
	1. 从Compact Height Field的Min点向Max点方向枚举Span，枚举结束则去3；
	2. 当前Span距离边缘的距离为以下四个数的最小值：
		左方Span距离边缘的距离 + 2；
		左后方Span距离边缘的距离 + 3；
		后方Span距离边缘的距离 + 2；
		右后方Span距离边缘的距离 + 3；
		计算完成后返回1；
	3. 从Compact Height Field的Max点向Min点方向枚举Span，枚举结束则去5；
	4. 当前Span距离边缘的距离为本身和以下四个数的最小值：
		左前方Span距离边缘的距离 + 3；
		前方Span距离边缘的距离 + 2；
		右前方Span距离边缘的距离 + 3；
		右方Span距离边缘的距离 + 2；
		计算完成后返回3；
	5. 结束。

在完成Distance Field的计算后，将使用Watershed算法对Compact Height Field划分区域。
Watershed算法的核心包括两步操作，其一为泛洪，即令当前的水源向四周扩散；其二为寻找新的水源，即根据高度限制，将符合条件并且仍没被水覆盖的区域设置成新的水源。整个Watershed算法的详细流程如下所示。

Watershed算法
输入：Distance Field，Step
输出：Regions
	1. 记MaxDist为Distance Field中的最大值，Iter为每次泛洪迭代次数，Step为步长，则WorkingInterval为(MaxDist – Step, MaxDist];
	2. 每轮计算WorkingInterval的左右端点均减Step，若右端点小于等于0，则去5；
	3. 泛洪：枚举所有离边缘的距离在WorkingInterval范围内的Span，若其周围Span已被水覆盖，则令该Span也被同样的水覆盖，反复枚举Iter次，结束后去4；
	4. 寻找新的水源：枚举所有3结束后仍没被水覆盖的Span，将它们设置为新增的水源，并使用BFS算法，将相邻的水源合并成一个，返回2；
	5. 结束。

在下中，以一个简单的场景为例，详细展示了Watershed算法每一步的效果。其中，不同的颜色表示不同水源泛洪覆盖的区域，同时每轮循环中新增的水源用红色框特别标出。下图的左上角图(1)中展示了Distance Field，由此可知MaxDist = 6，若设置Step = 2，Iter = 2，则后续过程如下图(2)-(4)所示。

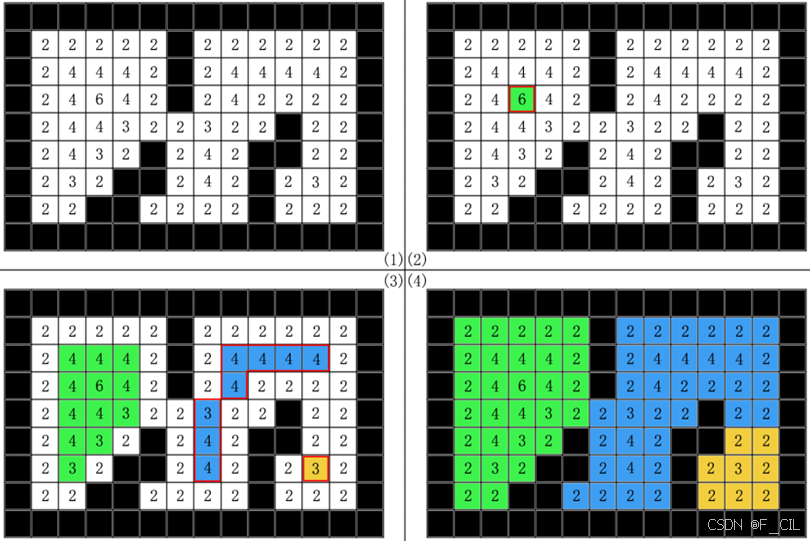
上图(2)为第一轮计算，此时WorkingInterval = (4, 6]，场上并没有水源，所以泛洪步骤跳过。在随后的寻找新水源环节中，找到一个距离为6的格子，将其标记为新的水源。
上图(3)为第二轮计算，此时WorkingInterval = (2, 4]，在泛洪步骤中，绿色的水源覆盖了其周围距离在限制范围内的格子，在寻找新水源环节中，找到了蓝色和黄色的两个新的水源。
上图(4)为第三轮计算，此时WorkingInterval = (0, 2]，在泛洪步骤中，三个水源填满了整个场景。故而，不再有新的水源。随后，在第五轮计算（未画出）中，WorkingInterval = (-2, 0]，结束算法。

区域轮廓生成

在完成区域划分后，我们将范围较大的Compact Height Field分割成了若干尺寸适当，形态简单的子区域。随后，要构建出每个区域的轮廓线，也即是多边形网格的初步形成。

上图所示为区域划分的效果图，而下面两幅图则分别表示上图对应的原始轮廓线（Raw Contours）效果和简化轮廓线（Simplified Contours）效果。

1. 原始轮廓线
本文使用Marching squares算法的思想去构建每个区域的原始轮廓线，这是一个常用于计算机图形学中的算法，其功能是根据矩阵网格点数据生成等值面。
该算法模拟了沿着区域边缘走一圈的流程，类似将一个机器人放置在一个边缘Span中（即该Span与周围4个Span所属的区域并不完全相同），并按照相应指令去移动，算法过程如下所示。

构建原始轮廓线
输入：Compact Height Field, Regions
输出：Raw Contours
   1. 如果面前的Span与当前Span同属于一个区域，就向前移动到面前的Span上，随后向左转；
   2. 如果面前的Span与当前Span不属于一个区域，就右转；
   3. 如果当前走到了与出发点相同的Span上，就结束。

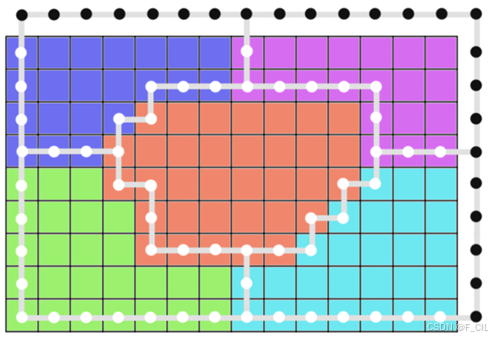
如下图所示为使用10张子图详细展示了原始轮廓线的生成步骤，图中 “黑色三角符号” 表示当前所在的Span，灰色线和白色点表示构建中的Raw Contour。其中，图(1)为区域划分的结果，图(2)-(3)与(6)-(7)描述了算法中步骤2的效果，图(4)-(5)与(8)描述了算法中步骤1的效果。图(9)为红色区域完成了轮廓线构建，图(10)为所有区域完成了轮廓线构建。

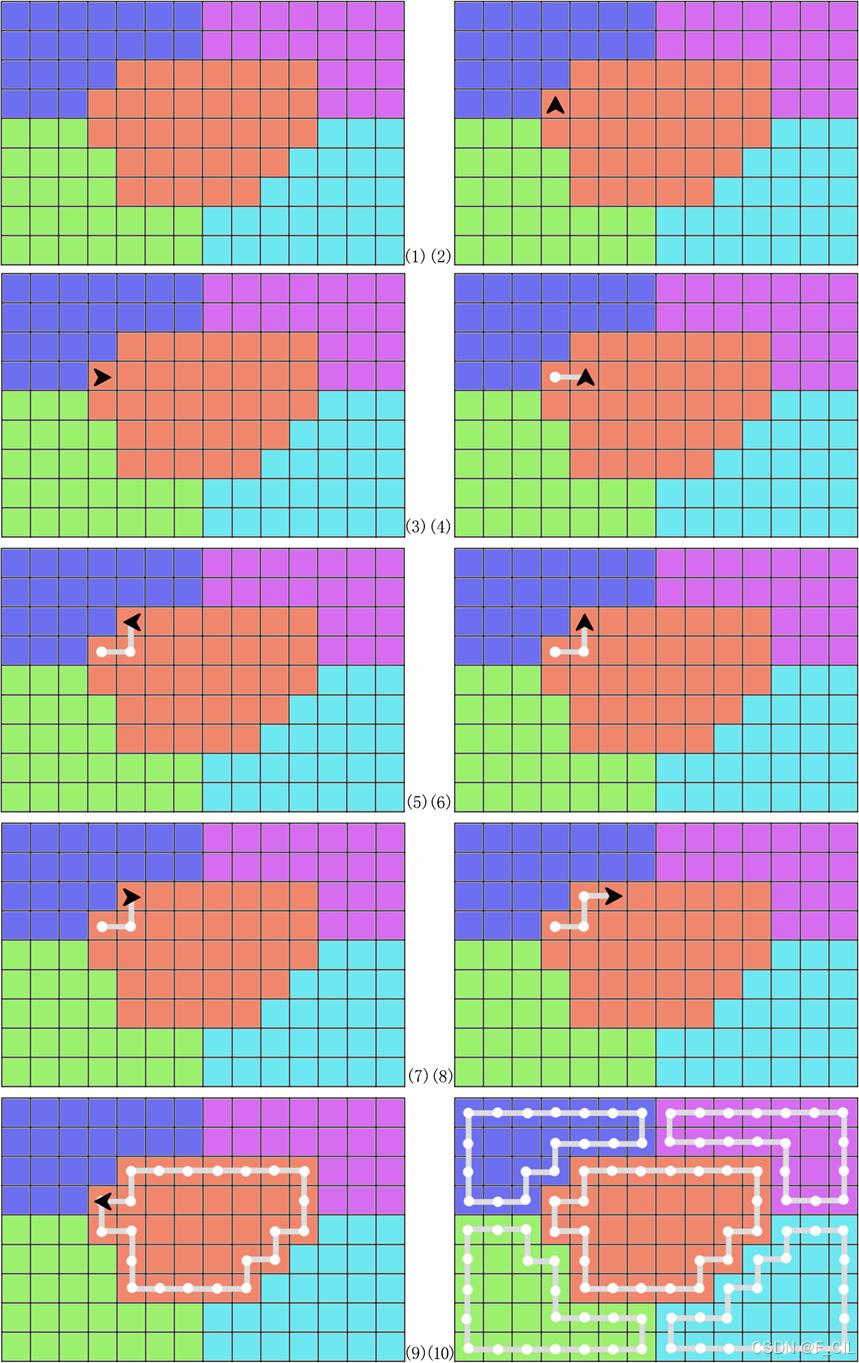
由图(10)不难发现，不同区域的轮廓线是完全独立的。这样，一方面极大地增加了轮廓线中点的数量，另一方面使得轮廓线之间的相邻关系难以建立。故而，可以优化构建轮廓线过程中取点的逻辑，具体方式如下：

- 若当前Span与左方Span区域不同，轮廓点取其前方Span坐标；
- 若当前Span与前方Span区域不同，轮廓点取其右前方Span坐标；
- 若当前Span与右方Span区域不同，轮廓点取其右方Span坐标；
- 若当前Span与后方Span区域不同，轮廓点取其自身坐标。

下图所示为使用优化后的取点逻辑构建的轮廓线。不难看出，相邻的区域会共用一部分点，这在让图中的点数总量大幅减少的同时，很容易建立起相邻轮廓线的连接关系。不过要注意的是图中黑色的点，这些超出了区域界限的点只会出现在前方和右方，在后续阶段需要特殊处理掉以防止最后生成的NavMesh包含了一些不想要的区域。

2. 简化轮廓线
经过优化的Raw Contours仍不能够直接用于生成凸多边形网格，首先它仍包含太多的点，其次它有很多锯齿状的边界。
为此，本文将使用Ramer-Douglas-Peucker（RDP）算法化简Raw Contours。RDP算法，又称Douglas Peucker算法或迭代终点拟合算法，其基本思想是在原点集中选择尽量少的点，并且最小化新点集组成的多边形与原多边形的差距。RDP算法的详细流程如下所示。

这里再补充一下，这种文字描述的算法流程也是毕设论文的要求，但是我其实写的比较烂，甚至可能存在错误，大家可以主要看图解，或者直接去项目里看代码。
Tips：整个算法部分的图解都是我拿 ps 一点点画出来的 QwQ

RDP算法
输入：Raw Contours, Deviation
输出：Simplified Contours
	1. 在Raw Contour中选择两个距离最远的点A和B添加进Simplified Contour中作为起始节点；
	2. 定义递归方法Fun(i, j): 在i -> j的所有点中找到距离线段ij最远的点k，若k距离ij的距离超过Deviation，则将k添加进Simplified Contour中，并调用Fun(i, k)和Fun(k, j)； 
	3. 调用Fun(A, B)化简A -> B区间；
	4. 调用Fun(B, A)化简B -> A区间；
	5. 结束。

RDP算法的具体效果下图所示。图中，灰色的点和线表示Raw Contour，红色的点和线表示当前的Simplified Contour，蓝色的点表示算法步骤2中选取的k点。不难看出，Raw Contour中包含了26个顶点，并且有一些锯齿状的边界，而经过化简后的Simplified Contour中仅有6个顶点，并且将一些锯齿装的边界用单条线段代替。

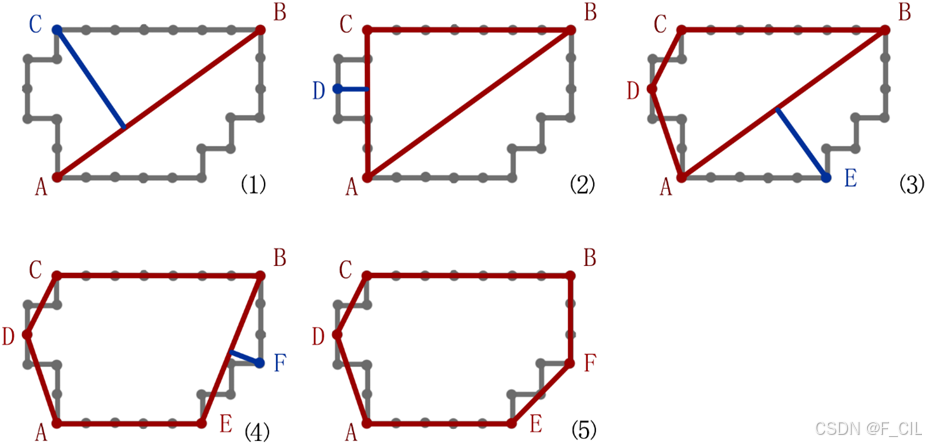
3. 合并孔洞

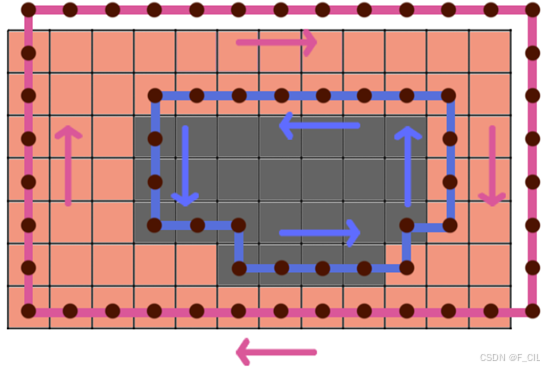
在一些复杂的场景中，可能会出现一些区域内有孔洞或区域内包含了其他区域的情况，如上所示，红色格子表示一个区域，灰色格子表示该区域内包含的一块障碍物。不难看出，此时红色区域的轮廓线有紫红色和蓝色两条。根据计算Raw Contours的算法，可以知道紫红色的轮廓线上的顶点是逆时针存储的，而蓝色轮廓线上的顶点是顺时针存储的。

经过简化后的轮廓线如下图所示，此时仅需计算每个多边形的有向面积。由于紫红色轮廓线区域顶点逆时针排布，因此有向面积大于0；而蓝色轮廓线区域顶点顺时针排布，所以有向面积小于0。于是，可以根据轮廓线的有向面积来判断一个轮廓线是不是孔洞的轮廓线。

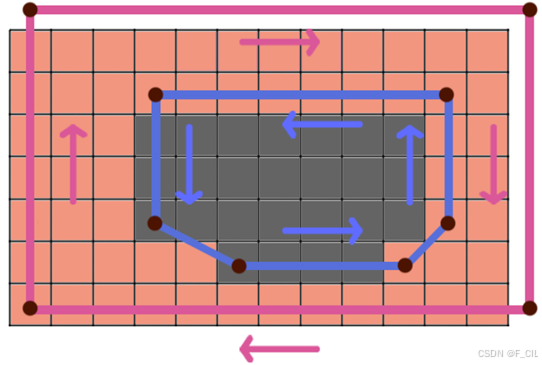
合并孔洞的效果如下图所示，将四边形FIHG合并为Hole，在其中选择一个顶点F，在外轮廓AEDCB上选择一个顶点A，由于AF外轮廓或Hole上的任意非A, F相邻边相交，因此可以连接AF，并将FIHG上的顶点反转顺序，实现将Hole与外轮廓合并成一个多边形。

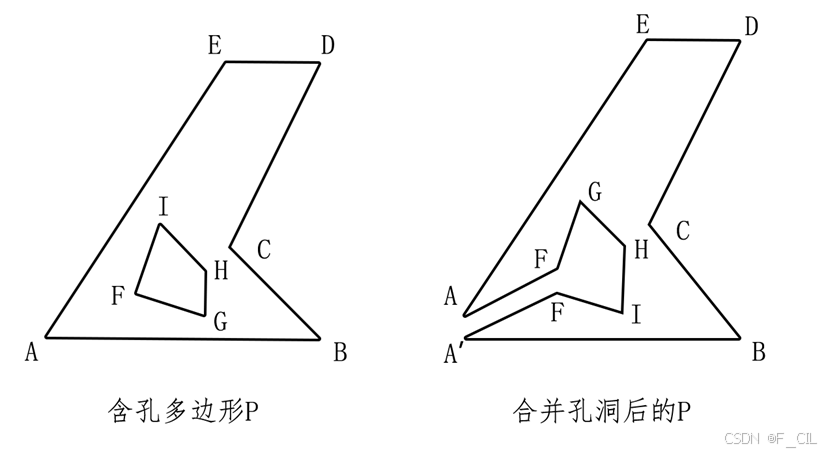
注解，关于孔洞的处理算法，@Mhypnos 用户提出了一些不同的观点，暂时贴在下面，我本来回复说会确认一下之后改进一下算法来着，但是一直忙（懒），所以我先把内容贴在这里，读者看到此处可以自行思考一下如何处理这种情况。
@Mhypons：
“关于有孔多边形，假设你的例子里，划分出的∠AFG，如果是凹点，那需要从F点出发找内部对角线，这个对角线和新增的AF的相交判断怎么处理，如果是往上，与AF是不相交，如果是往下，与AF又应该是相交的，这个就矛盾了。要如何处理呢”
“特判应该会有问题，特判要知道具体分割线，相当于手动分割了， 自动分割就失去了意义，对于实际项目，孔洞数量多的情况下不太现实。如果凹角是公共点，那新的内部对角线判断和其他边相交的时候，要忽略复制点连接的两条线。例如从F出发寻找的内部对角线，相交线判断要忽略IF和FA，因为线必须在∠AFG内，从A出发的线，相交线判断要忽略EA和AF，因为线必须在∠FAB”
原帖：多边形分割成若干凸多边形（NavMesh的初步形成） 的评论区

构建凸多边形网格

在为每个区域生成轮廓并简化后，可以得到了若干多边形的集合。在此节，要将所有的多边形转换为凸多边形，也即是NavMesh的雏形。对于大多数对地形精细度要求不高的游戏来说，完成这一步所得到的凸多边形网格集合（PolyMesh Field）就已经完全可以用于寻路了。
PolyMesh Field的效果如下图所示。图中，不同颜色的凸多边形表示他们从属于不同的区域。

将任意多边形分割成若干凸多边形的常见方法有很多，本文采用业界最常用的耳切法（Ear Clipping Algorithm）。耳切法是一种三角剖分算法，它可以将任意多边形切分成若干三角形；随后，再将这些三角形合并成凸多边形，就完成了将任意多边形转换成若干凸多边形的任务。耳切法的详细过程如下所示。

耳切法三角剖分
输入：Simplified Contours
输出：PolyMesh Field (Triangles形态)
	1. 枚举Simplified Contour中的全部顶点，检查以该顶点是不是凸点；
	2. 逐个枚举Simplified Contour中的凸点i，若此时只剩三个点则去5； 
	3. 记i的两个相邻点为a、b，取使得|ab|最小的i；将以a、i、b为顶点的三角形加入到Triangles集合中，并将其在Simplified Contour中删除；
	4. 检测切去顶点i后的a、b两点是否变成了凸点，返回2；
	5. 将最后三个点标记为一个三角形并添加到Triangles集合中，结束。

下图所示为用9张子图描述了耳切法三角剖分的过程。其中，图(1)为一凹多边形，图(9)为三角剖分的结果。图(2)-(8)中红点为当前多边形中的凸点，蓝点为要被切除的凸点，蓝边表示切边。易知对于任意n个顶点的多边形，会被切分成n-2个三角形。

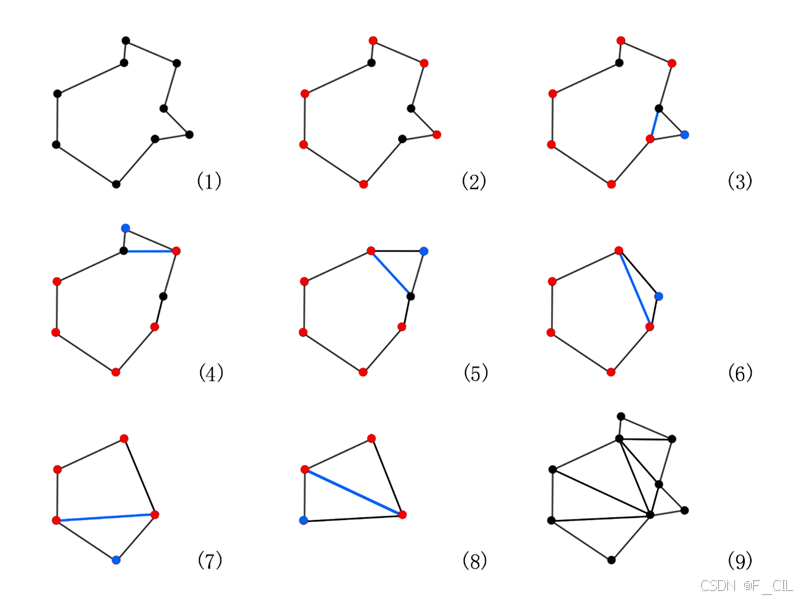
在利用耳切法对一个多边形切分后，可以得到若干三角面。由于三角形一定是凸多边形，因此理论上此时的Triangles集合就已经可以作为NavMesh用于寻路了。但显然此时多边形的数量较大，会使得寻路的效率降低。所以，需要尽可能多地将三角面合并成更大的凸多边形。合并过程如下所示。

三角形合并算法
输入：PolyMesh Field (Triangles形态)
输出：PolyMesh Field
	1. 枚举所有多边形，执行2判断两两是否可以合并，若可合并去3，若均不可合并则去4；
	2. 若两个多边形无共享边（不相邻）或共享边两侧形成的角为凹角，则不可合并，否则可以合并；
	3. 合并这两个多边形；
	4. 结束。

如下图所示为使用红色和蓝色表示两个相邻的多边形。在图(1)中，可以看到两个三角形公共边上方顶点在合并后对应的外角∠α为凹角，所以此时两个三角形不可以合并。而图(2)中，两个三角形公共边顶点合并后对应的角依然是凸角，也就意味着这两个三角形合并后是一个凸多边形，故而可以合并。对于两个凸多边形是否合并的判断依然可以利用此方法，例如图(3)中的两个凸多边形不可合并，而图(4)中的两个凸多边形可以合并。

如下图所示为上方展示耳切法算法过程图中多边形经过合并算法的结果。图(1)中相同颜色的三角形会被合并成一个大的凸多边形，图(2)为合并后的效果。

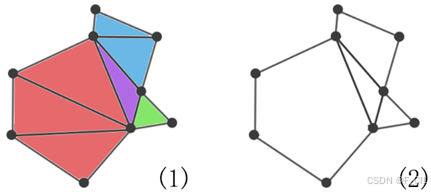
补充高度细节

对于一些地形丰富的场景，仅仅使用上一节中生成的PolyMesh Field可能会存在定位不精确的问题。如下图所示，由于Agent可以在整个场景中任意移动，此时生成的PolyMesh Field并没有很好地表达出场景在高度方向上的细节信息。

为PolyMesh Field补充高度细节之后的效果如下图所示，可以看到经过处理后的多边形网格可以比较精细地贴近实际地形。

不过，由于一方面在大部分游戏中Agent的移动并不仅依赖导航模块提供的路径点，而是以其作为基础移动方向，结合物理碰撞效果最终得到Agent最终的移动方向；另一方面，补充高度细节极大地增大了多边形的数量，会降低寻路的效率，因此本节的内容并非必不可少的操作。
补充高度细节的过程由两部分组成：边采样、面采样。
1. 边采样
边采样指的是在多边形的每条边上选取若干采样点，再使用RDP算法决定最后将使用哪些采样点分割原边。具体的流程如下所示。

边采样
输入：PolyMesh Field，Compact Height Field，SampleDistance
输出：PolyMesh Field (边采样后)
	1. 枚举PolyMesh Field的每个多边形，枚举结束则去6；
	2. 枚举多边形的每条边，枚举结束则去5；
	3. 在边上每隔SampleDistance放置一个采样点，并在Compact Height Field中找到采样点对应的实际高度；
	4. 使用RDP算法计算对于该边应当保留哪些采样点；
	5. 使用Triangulate Hull算法三角剖分被采样点修正后的多边形，返回1；
	6. 结束。

对于一条边采样的RDP算法过程如下图所示。

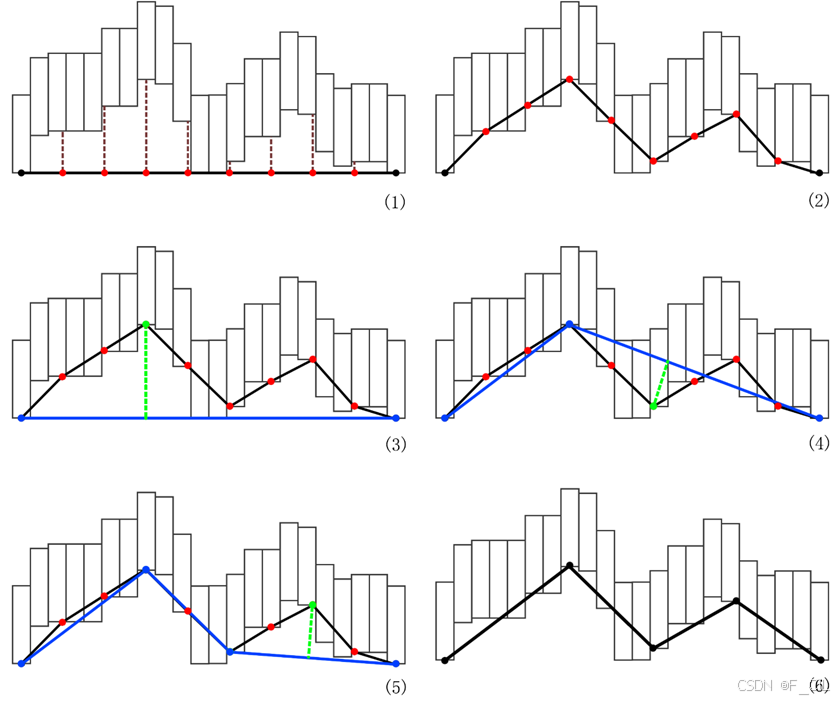
其中，图(1)中左右两个黑色的点以及他们的连线代表了多边形中的一条边，而上方错落的长方形条代表了Compact Height Field中的Span，下方中间8个红点为采样点，棕色的虚线将每个采样点指向了它们对应的真实高度，也即是Span的坐标。图(2)绘制了通过8个采样点将原始边转换成了一条折线，要对这个折线执行RDP算法简化。图(3)-(5)中蓝色的点表示当前Simplified集合中的点，蓝色的边表示由这些点连成的边，绿色的点表示与化简后的边距离最远，且距离超过Deviation的点，也就是将要被添加进Simplified点集中的点。图(6)为该边经过边采样后的最终结果。
对于一些面积较小的多边形，通常只需对其进行边采样即可。在边采样完成后，需要使用三角剖分算法将其转变成若干三角面。在上一节中，使用耳切法实现了将任意多边形三角剖分。不过在这一节中，面对的是凸多边形的三角剖分，所以可以采用效率更高的Triangulate Hull算法。该算法基于贪心思想，仅使用凸多边形边缘上的顶点，并尽可能减少剖分后三角形的总周长。算法的详细步骤如下所示。

Triangulate Hull算法
输入：Convex Polygons in PolyMesh Field
输出：Triangles
	1. 在凸多边形中枚举顶点A，计算以该顶点以及相邻两点（B、C）形成的三角形的周长，取周长最短的Triangle A；
	2. 将Triangle A切掉；
	3. 以B、C为新的三角形顶点，比较这两个三角形周长，取周长最小的那个三角形（假设为Triangle B）；
	4. 将Triangle B切掉；
	5. 若凸多边形中仅剩3个点，则最后三个点形成一个三角形，否则返回3；
	6. 结束。

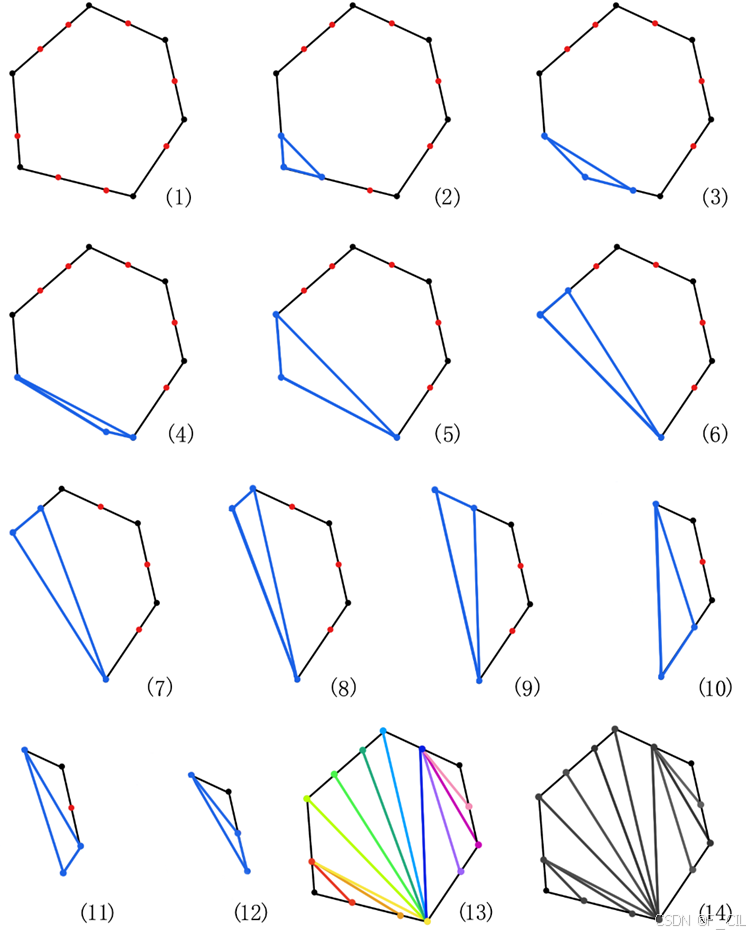
Triangulate Hull的效果如下图所示。其中，图(1)中黑色点表示PolyMesh Field中一个凸多边形自身的顶点，红色点表示边采样步骤中新增的点。图(2)-(12)为Triangulate每一步的效果，其中蓝色点和边标记出的三角形为算法步骤2或4中选择切下的三角面。图(13)-(14)为该凸多边形三角剖分的结果，在图(13)中不同颜色的边分别表示图(2)~(12)中每一步使用的切边。

2. 面采样
对于面积较大的凸多边形来说，仅进行边采样并不能让网格足够贴近原始地形。这时，需要在凸多边形内部播撒若干采样点，同样使用RDP算法思想决定每个采样点是否保留。并在最后使用Delaunay Hull算法处理凸多边形以及其内部的采样点，将其变成由若干三角形组成的面。具体流程如下所示。

面采样
输入：PolyMesh Field，Compact Height Field，SampleDistance，Deviation
输出：Triangle Mesh
   1. 枚举PolyMesh Field中的每个多边形，枚举结束则去6；
   2. 在多边形内部铺设边长为SampleDistance的网格，将网格顶点作为采样点，并在Compact Height Field中找到采样点对应的实际高度；
   3. 计算每个采样点距离多边形的距离；
   4. 按照距离从大到小枚举所有仍未被选中的采样点，如果距离大于Deviation则将该采样点选中，没有采样点可选则返回1；
   5. 使用Delaunay Hull三角剖分当前多边形，返回3；
   6. 结束。

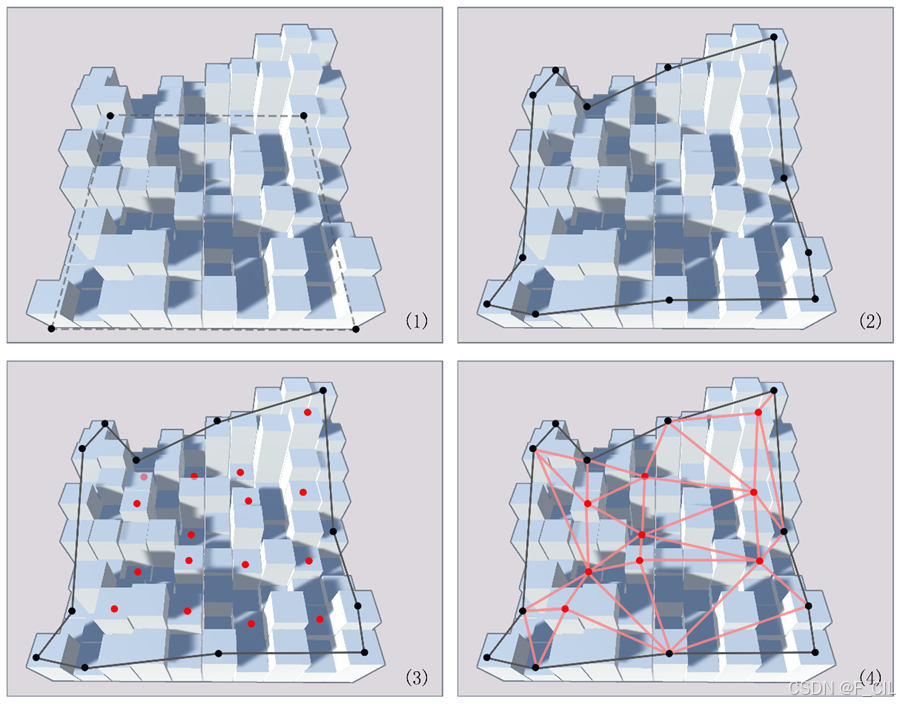
面采样算法的具体效果如下图所示。由于Compact Height Field不便于观察，故而使用Solid Height Field来演示。图中，错落的长方体表示Solid Span，即地形所占用的体素区间，根据Compact Span与Solid Span的关系易知Solid Span的Top即为Compact Span的Floor，也就是Agent可以移动的表面。图中的四个黑点与虚线边表示PolyMesh Field中的一个凸多边形；图(2)为边采样后的多边形，可以看到在原多边形的边上添加了很多顶点，用于拟合实际地形；图(3)中的红色点表示在多边形内部播撒的采样点；图(4)则为完成面采样算法后得到的Triangle Mesh，可以看到选择了一部分采样点，并将整个多边形三角剖分成了若干连接的三角面。与图(1)中的多边形相比，图(4)中的Triangle Mesh可以更好地拟合错落有致的地形变化。

在面采样算法步骤5中，使用Delaunay Hull算法计算三角剖分。该算法能够在O(nlogn)的时间复杂度下（n为顶点个数），将平面点集分割成若干三角形。其基本思想是先对点集进行径向排序，然后从中心点开始逐步构造一个不重叠的三角形网，保证每个三角形的外接圆内不包含其他点。这种剖分具有最优性质，即最大化最小角。Delaunay Hull算法的详细步骤如下所示。

Delaunay Hull
输入：多边形顶点，面采样点
输出：Triangles
	1. 对n个点进行径向排序，即按照它们到中心点的距离从小到大排列。
	2. 从中心点开始，依次取出三个点，构造一个三角形，并将其加入sweep-hull中。
	3. 继续取出下一个点，如果它在sweep-hull的外部，那么找出所有与它相交的三角形，并删除它们的公共边，然后将这个点与剩下的顶点连接，形成新的三角形，并加入sweep-hull中。
	4. 重复步骤3，直到所有的点都被处理完毕，此时得到一个不重叠的三角形网，即sweep-hull。
	5. 对sweep-hull中的每条边，检查它是否满足Delaunay条件，即它的两个相邻三角形的外接圆内不包含其他点。如果不满足，那么翻转这条边，即将它替换为它的对角线，并更新相邻三角形。
	6. 重复步骤5，直到所有的边都满足Delaunay条件，此时得到Delaunay三角剖分。

Delaunay Hull的效果如下图所示。图中，红色的点为被选中的面采样点，黑色点为多边形自身顶点。可以看到，经过Delaunay三角剖分获得的三角面集合具有空圆性质，即任意一个三角面的外接圆范围内都不包括其他点。

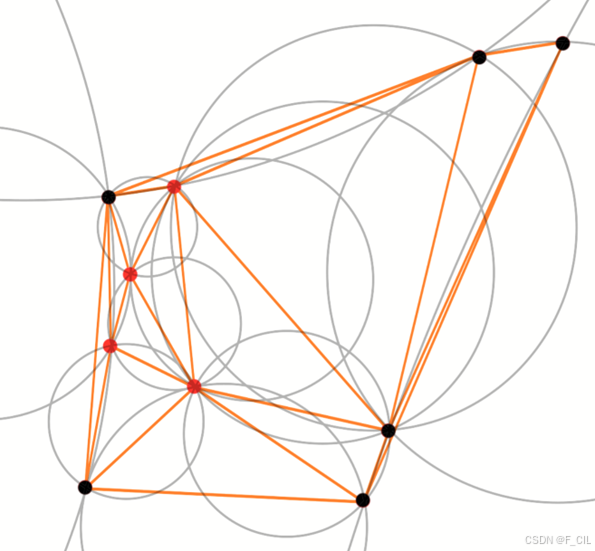
Tips：就这个图不是 Ps 画的，是用 Python 画的，2333

A*寻路算法

A*算法是一种用于寻找从一个节点到另一个节点的路径的搜索算法，它是一种启发式搜索算法，或者说是一种最佳优先搜索算法。A*算法在效率和准确性方面比其他工具更优秀，因此它在没有预处理图的情况下被广泛使用。
A*算法是对迪杰斯特拉算法的一种改进，它针对单一目标进行了优化。迪杰斯特拉算法可以找到起点到所有位置的路径，而A*算法可以找到起点到终点的最短路径。A*算法使用公式f(n) = h(n) + g(n)，其中h(n)为启发函数，表示n点与终点的估计距离，启发函数的优劣对A*算法的效率有很大的影响；g(n)为从起点到n点的实际距离。A*算法根据f(n)的大小选择下一个目标点，也即是优先考虑看起来更接近目标的路径点。A*算法的详细流程如下：

Tips：网上 A* 的教程多如牛毛了，其中不乏精良制作，大家如果对 A*算法不熟悉的话，建议移步他人博客学习，我这里写的就是一坨，请见谅。当然如果大家觉得网上其他人写的看不懂，也可以评论区 Push 我专门写一下寻路部分的文章，嘿嘿。

A*算法
输入：图G(n,edge)
输出：由G中点组成的路径
	1. 定义一个启发函数h(n)，用于估计任意节点n到目标节点的代价。
	2. 创建一个空的优先队列Q，用于存储待扩展的节点，按照f(n) = g(n) + h(n)的值从小到大排序，其中g(n)是从起点到节点n的实际代价。
	3. 将起点start加入Q，并设置g(start) = 0。
	4. 如果Q不为空，重复以下步骤：
		a. 从Q中弹出最小的f(n)对应的节点n。
		b. 如果n是终点dest，返回成功，并输出路径。
		c. 否则，对于n的每个邻接节点m：
			① 计算g(m) = g(n) + edge[n][i].val，其中i是m在edge[n]中的索引。
			② 如果m已经在Q中，且g(m)不小于之前的值，跳过这个邻接节点。
			③ 否则，更新g(m)和f(m)，并将m加入或更新在Q中。
	5. 如果Q为空，返回失败，没有找到路径。

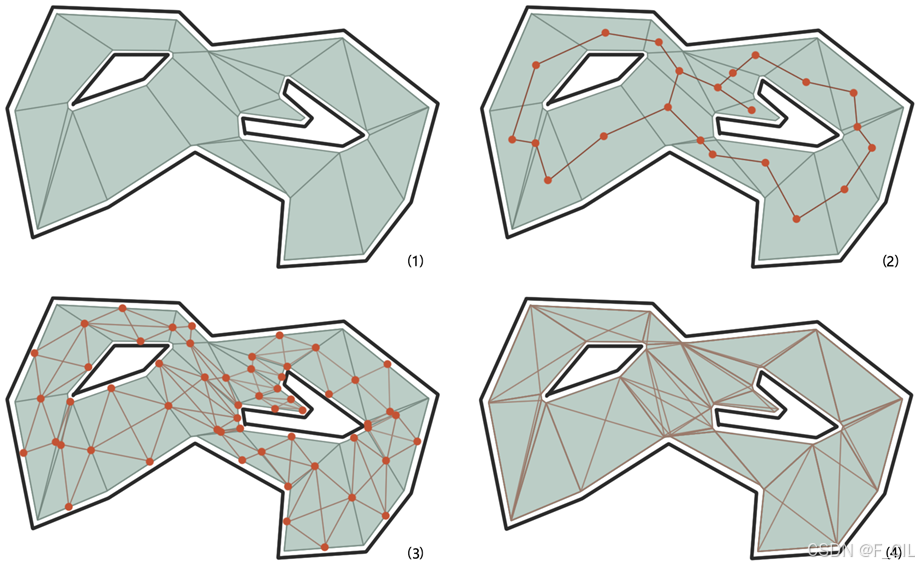
由于导航网格并非点，所以在执行A*算法寻路时，仍需要从导航网格中抽象出一些点，常见的方式有基于顶点、基于边中点、基于网格中心点三种方式。每种方式的效果如下图所示，图(1)中较粗的黑色线条代表障碍物，浅绿色面代表导航网格，深绿色细线画出了导航网格中的每个凸多边形。图(2)中红点表示每个凸多边形的中心点，棕色细线为相邻凸多边形中心点的连线。图(3)中红点表示凸多边形每条边的中心点，棕色细线为边中心点之间的连线。图(4)中棕色细线表示凸多边形顶点之间的连线，由于线条密集故而没有使用红点额外标记每个凸多边形的顶点。从图中不难发现，仅使用凸多边形中心点用于寻路，点和边的数量较小，算法执行效率高，但是路径比较生硬，并且得到的路径并非最短路。而使用边中点和顶点用于寻路能够得到更好的路径，但是由于点和边数量的增加，在执行效率上会差一些。其中使用顶点寻路会使Agent一直贴着障碍物边缘移动，而使用边中点寻路能够使Agent更多的横穿凸多边形移动，并且使用边中点寻路可以使用拉绳法优化路径，所以在本文中，使用边中点进行A*算法寻路。

拉绳法优化路径
仅使用边中点寻路得到的路径通常并不是最短路，并且会比较生硬，如下图所示，图中绿色点代表起点，蓝色点代表终点。浅蓝色线段表示通过边中点寻得的路径，不难发现这并不是最短路，且路线曲折生硬。实际上的最短路由紫色线绘出。

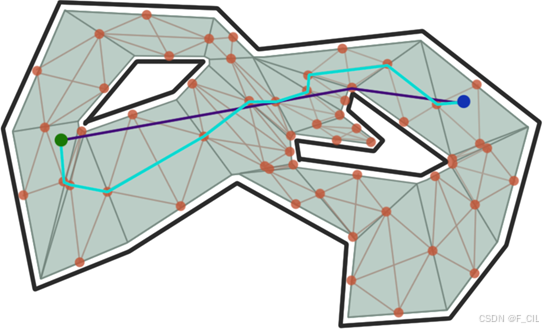
拉绳法/漏斗法（Funnel Algorithm）是一种平滑路径的方法，它可以消除A*寻路算法产生的多余的拐角点，使得路径更加直线化。拉绳法的基本思想是，从起点开始，沿着A*寻路的路径，枚举路径点所在边的两个端点（形状像一个漏斗），不断选择能让漏斗口变小的点，但当漏斗两边交叉时，说明找到了一个新的拐点。然后以该拐点为起点继续重复这个过程，直到到达终点。这样就可以得到一个更加平滑的路径。详细过程如下所示。

拉绳法
输入：路径点
输出：平滑后的路径点
	1. 将起点添加到平滑后的路径点集合中，并标记为第一个拐点Q，定义漏斗左侧点为L，右侧点为R；
	2. 从起点开始逐个枚举路径点P_i，枚举结束去7；
	3. 记P_i左侧顶点为A，右侧顶点为B；
	4. 记P_(i+1)左侧顶点为A'，右侧顶点为B'，若∠A' QB<∠AQB则令L移动到A'，若∠AQB'<∠AQB，则令R移动到B'，返回2继续迭代；
	5. 若R移动到了L左侧，则将L点标记为新的拐点Q，并添加进平滑后的路径点集合中，返回2继续迭代；
	6. 若L移动到了R的右侧，则将R点标记为新的拐点Q，并添加进平滑后的路径点集合中，返回2继续迭代；
	7. 结束

如果把原路径看作一根绳子，则用该算法平滑路径就好比将原绳子拉直了，所以该算法可以被叫做拉绳法。同理，在算法求解过程中，会不停的考虑路径点左右两侧端点之间的夹角，像一个漏斗一样，故而也常被称作漏斗法。
如下图所示，为整个拉绳法的详细运行流程，在图(1)中，绿色点表示起点，蓝色点表示终点，浅蓝色线表示依据边中点A*寻路求得的路径，紫色线表示经过拉绳法优化后的路径。图(2)-(5)对应算法3~4步，可以看到由紫色和深蓝色两个线段构成的漏斗夹角在不断变小。图(6)对应算法4、6步，蓝色虚线表示由于∠AQB’>∠AQB，所以蓝色线无法移动，紫色线移动后出现L到R右侧的情况，故而用红色三角形表示新增了一个拐点。图(7)-(14)为后续步骤，在这些图中使用红色线表示当前平滑后得到的路线。

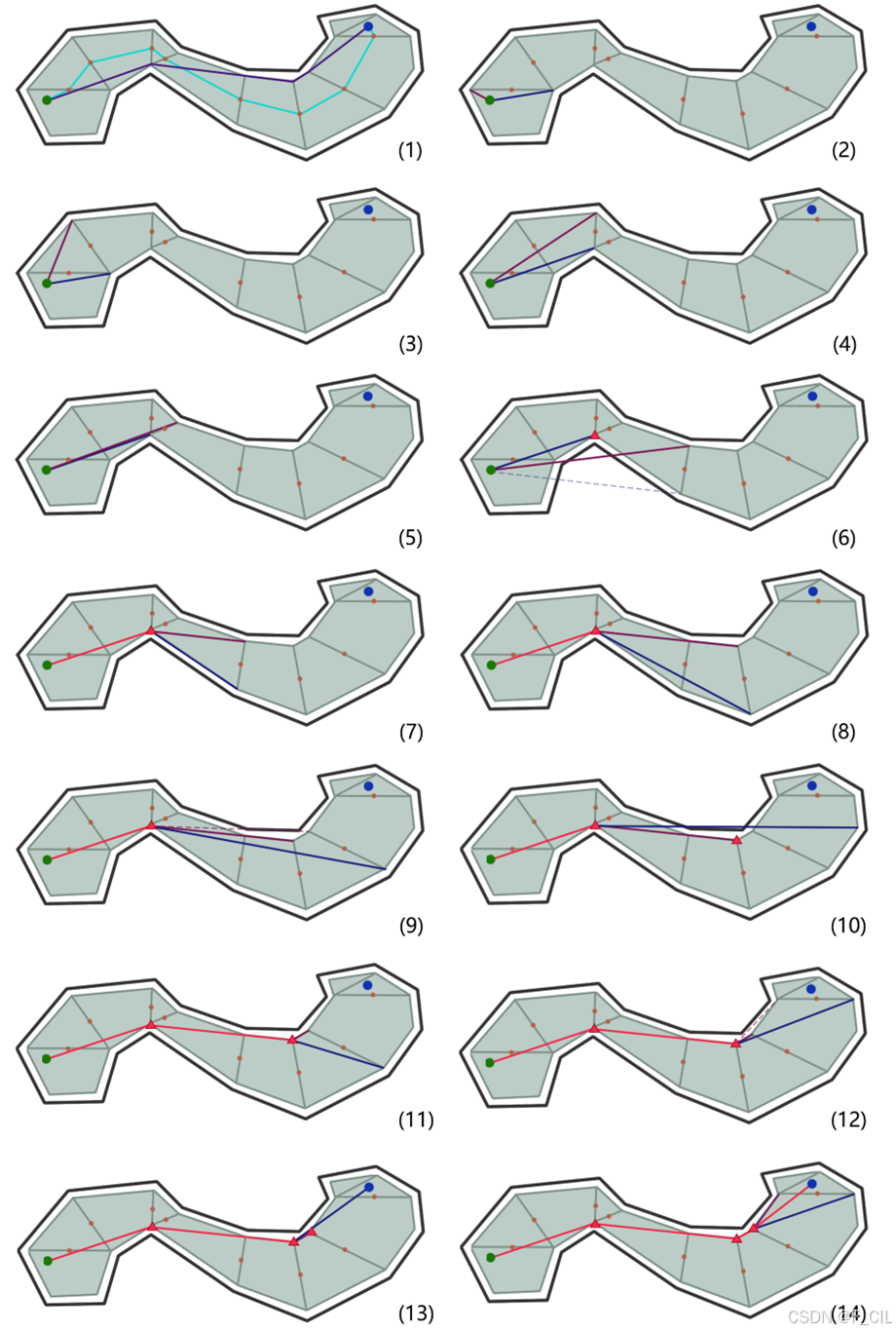
值得注意的是，使用边中点寻路 + 拉绳法优化路径仍然不能保证最终获得的路径就是最短路，尤其是在导航网格中凸多边形尺寸过大时。在本文中通过导航网格生成时限制凸多边形的大小的方式使得最终求得的路径与最短路的差距尽可能小。

ORCA避障算法

整个避障部分其实在毕设制作周期内没来及做，QwQ，但是嘛，论文上肯定还是得水一点的，这边就不展示了，写的一坨，大家想学习这个算法的话，可以在网上自行查阅相关资料。

以上部分就是整个导航网格生成相关算法的全部内容了，这里再贴一下该部分的 UML 类图：

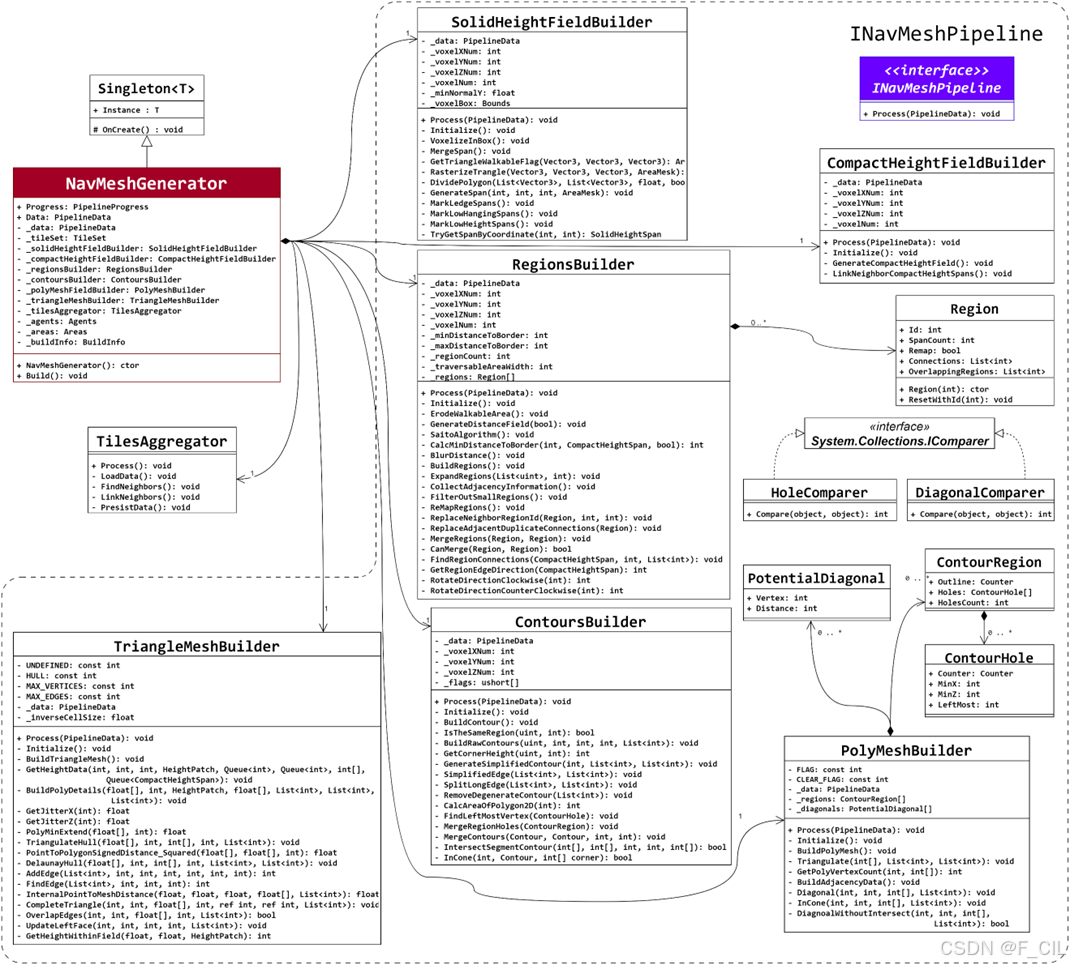
图片展示

导航网格生成程序实现流程图：

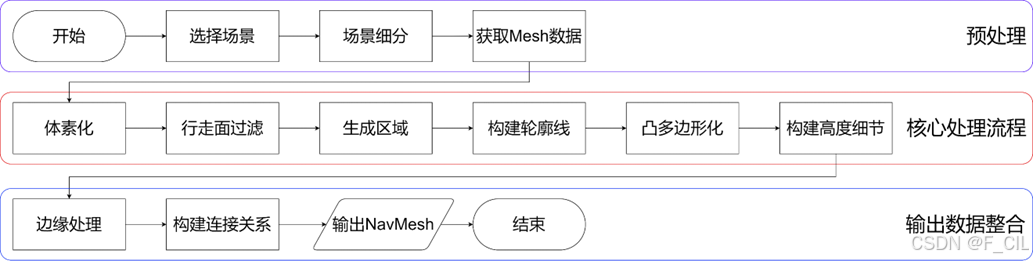
说来惭愧，把大场景切分成多个 Tile 我倒是写了，但是把多个 Tile 的 NavMesh 合成成一张大的 NavMesh 没写 QwQ

数据可视化模块运行效果

NavMesh生成时，会在被处理场景同一路径下建立后缀为“_Navigation”的文件夹，并在其中存放NavMesh数据。在完成NavMesh生成后，会自动将展示功能开启。用户也可以通过菜单栏按钮Navigation - Show Gizmos，在任何时候启动展示功能。

用户可以在Scene窗口右下角的Gizmos Type菜单中，选择要展示的内容。首先要选择要展示Agent，然后选择要展示的数据类型，最后选择要展示Tile。

网格数据可视化
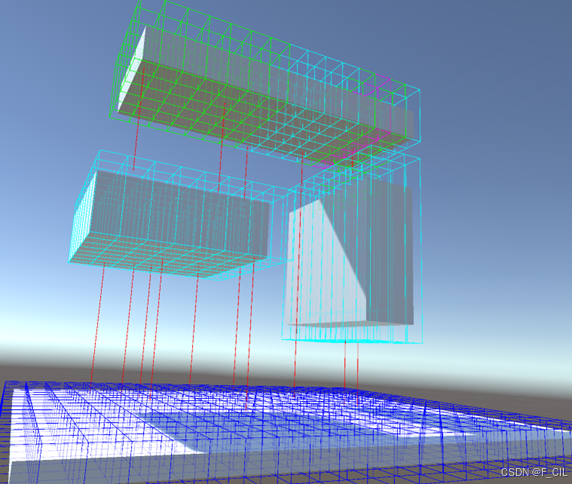
实行高度场（Solid Height Field）为体素化所得到的高度场数据，记录的是场景中被障碍物占据的区域，Solid Span从下向上串联起来。一个较复杂场景的Solid Height Field如下图所示，蓝色为最下层的Span，紫色为第二层Span，其他颜色表示更高层的Span。由于该游戏场景的地形是一小块一小块拼接而成的，所以部分地方存在相互覆盖的情况，导致理论上应该是被蓝色块覆盖的地面上也有一些紫色区域。这类细节问题会在后续流程中逐渐被过滤掉。

紧缩高度场（Compact Height Field）为对Solid Height Field过滤并反体素化后求得的Agent可行走的面，如下图所示，此时绿色块为Agent可行走的区域，红色块为Agent不可行走的区域。此时不难发现在上一步中地形块相互覆盖造成的影响已经不复存在。

距离场（Distance Field）为利用Saito算法处理Compact Height Field数据所得，记录的是每个Compact Span与边界的距离。如下图所示，图中颜色越红则说明距离边界越远，颜色越黑则说明距离边界越近。

区域（Region）为使用Watershed算法处理 Distance Field数据所得。它将场景划分成若干小的区域。如下两张图所示，分别表示复杂场景和简单场景经过区域划分后的效果，图中相邻的区域使用了不同的颜色去绘制。从图中不难看出划分的区域均符合章节2.4中提到的“形态简单”标准。

轮廓线（Contours）分为两部分，原始轮廓线（Raw Contours）和简化轮廓线（Simplified Contours）。Raw Contours为直接处理Regions数据，勾勒出每个Region的轮廓。Raw Contours的效果如下两张图所示，分别表示复杂场景和简单场景构建原始轮廓线后的效果，不难看出Raw Contours有着曲折的轮廓，这样能说明其中有着大量的顶点。

Simplified Contours为使用RDP算法简化处理Raw Contours数据所得，如下两张图图所示，分别表示复杂场景和简单场景简化轮廓线后的效果，Simplified Contours中每个顶点都使用不同颜色的小球绘制在场景中。不难发现它包含远少于Raw Contours的顶点以及更少的曲折。

凸多边形网格（Poly Mesh Field）即为将Simplified Contour所得的数据通过若干工序的处理，包括三角化、合并三角面建立凸多边形面、建立连接关系等，最终得到的凸多边形面的集合。我们在这个数据上利用A*算法为Agent提供寻路支持。如下两张图所示，不同颜色的多边形表示它们从属于不同的Region。

本工具支持多种尺寸的Agent，如下图所示为使用较大Radius的Agent生成的Poly Mesh Field。不难发现，一方面在上图中一些可以通行的区域已经变得不可通行，另一方面导航网格距离物体边缘的距离也更加大了。

高度细节（如Triangle Mesh）是对Poly Mesh Field中每个凸多边形进行采样后，形成的与游戏场景贴合精度更高的三角面网格。如下图所示，对于地形起伏细节丰富的场景，使用Poly Mesh Field往往在高度上无法较好的贴合游戏场景，这在大部分情况下并不会有什么问题，因为Agent的移动并不完全依赖导航网格。但是对于一些在高度上有特殊要求的游戏来说，可能需要更加精细的网格，如下第二张图所示，为Triangle Mesh的效果，不难发现，它用大量的三角面更精细的贴合了实际场景。

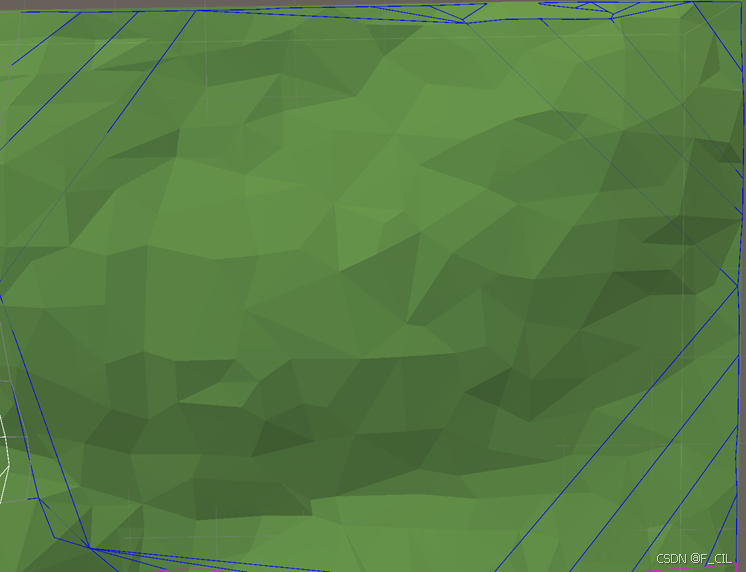
Tips: 就这个效果，我感觉其实不是特别对，我写的 TriangleMesh 的代码应该是有点 bug 的，主要不正确的点在于下方多了好多密集的小三角形

5.3.2测试寻路功能
在开启数据可视化功能后，会在场景中生成“NavMeshGizmos”物体，其包含两个立方体子物体，开发人员可以在场景中选择将它们移动到合适的位置上，点击开始寻路，即可得到如图5-24所示的效果。

到此就结束啦，感谢大家可以阅读到此处！
如有问题，希望可以友好交流，如果评论区施展不开，可以给我的邮箱发邮件：F_CIL@outlook.com