愤怒的导数：一点可导和邻域内可导能推出来什么？

愤怒的导数：一点可导和邻域内可导能推出来什么？

一、连续和可导的基本概念

01 连续的定义

设函数 $y=f(x)$ 在点 $x_0$ 的某一邻域内有定义，如果满足以下条件：
$$\underset{\Delta x\to 0}{\lim }\Delta y=\underset{\Delta x\to 0}{\lim }\left[f\left(x_0+\Delta x\right)-f\left(x_0\right)\right]=0或\underset{x\to x_0}{\lim }f(x)=f\left(x_0\right)$$
那么就称函数 $y=f(x)$ 在点 $x_0$ 连续；否则称 $f(x)$ 在点 $x_0$ 间断。

即函数在某点连续的充要条件是该点左极限右极限存在且相等并且等于该点函数值。

02 可导的定义

设函数 $y=f(x)$ 在点 $x_0$ 的某邻域内有定义，当自变量 $x$ 在 $x_0$ 处有增量 $\Delta x$ ( $x_0+\Delta x$ 点仍在该邻域内 )，

函数相应地有增量 $\Delta y=f\left(x_0+\Delta x\right)-f\left(x_0\right)$，则有：
$$f^{\prime }\left(x_0\right)\stackrel{def}{=}\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x}=\underset{x\to x_0}{\lim }\frac{f(x)-f\left(x_0\right)}{x-x_0}$$
如果极限存在，则称函数 $y=f(x)$ 在点 $x_0$ 处可导，此极限值称为函数 $y=f(x)$ 在点 $x_0$ 处的导数 ( 微商 ) 。

补充：二阶可导的定义

设函数 $y=f(x)$ 在点 $x_0$ 的某邻域 $U_{\delta }\left(x_0\right)$ 内有一阶导数 ( $f^{\prime }(x)$ 在点 $x_0$ 的某邻域内有定义 ) 。如果极限

$\underset{\Delta x\to 0}{\lim }\frac{f^{\prime }\left(x_0+\Delta x\right)-f^{\prime }\left(x_0\right)}{\Delta x}=\underset{x\to x_0}{\lim }\frac{f^{\prime }(x)-f^{\prime }\left(x_0\right)}{x-x_0}$ 存在，则称函数 $y=f(x)$ 在点 $x_0$ 处二阶可导，

即 $f^{\prime }(x)$ 在 $x_0$ 处一阶可导。此极限值称为函数 $y=f(x)$ 在点 $x_0$ 处的二阶导数，记为 $f^{\prime \prime }\left(x_0\right)$ 。

二、连续作为条件

01 某点连续

$$f(x)\text{ 在 }{x}_0\text{ 连续 }\Rightarrow \{\begin{array}{l}\text{ 1. }f(x)\text{ 在 }{x}_0\text{ 邻域内有定义 }✅\\ \text{ 2. }\underset{x\to x_0}{\lim }f(x)=f\left(x_0\right)✅\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }❌\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 可导 }❌\end{array}$$

02 某邻域内连续

$$f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }\Rightarrow \{\begin{array}{l}1.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 邻域内有定义 }✅\\ 2.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 邻域内处处连续 }✅\\ 3.f(x)\text{ 在 }{x}_0\text{ 可导 }❌\end{array}$$

03 某去心邻域内连续

$$f(x)\text{ 在 }{x}_0\text{ 去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内连续 }\Rightarrow \{\begin{array}{l}\text{ 1. }f(x)\text{ 在去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }✅\\ \text{ 2. }f(x)\text{ 在去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内处处连续 }✅\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 极限存在 }❌\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 可导 }❌\end{array}$$

三、可导作为条件

01 某点可导

$$f(x)\text{ 在 }{x}_0\text{ 可导 }\Rightarrow \{\begin{array}{l}\text{ 1. }{f}^{\prime }(x)\text{ 在 }{x}_0\text{ 有定义 }✅\\ \text{ 2. }{f}_{-}^{\prime }(x)=f_{+}^{\prime }(x)✅\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 连续 }✅\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }❌\\ \text{ 5. }f(x)\text{ 在 }{x}_0\text{ 邻域内可导 }❌\end{array}$$

02 某邻域内可导

$$f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内可导 }\Rightarrow \{\begin{array}{l}1.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }✅\\ \text{ 2. }f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内极限存在 }✅\\ \text{ 3. }f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内有定义 }✅\\ \text{ 4. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }❌\\ \text{ 5. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内极限存在 }❌\\ \text{ 6. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内有定义 }✅\end{array}$$

03 某去心邻域内可导

$$f(x)\text{ 在 }{x}_0\text{ 去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内可导 }\Rightarrow \{\begin{array}{l}\text{ 1. }{f}^{\prime }(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }✅\\ \text{ 2. }f(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内连续 }✅\\ \text{ 3. }f(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内极限存在 }✅\\ \text{ 4. }{f}^{\prime }(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }✅\\ \text{ 5. }f(x)\text{ 在 }{x}_0\text{ 有定义 }❌\\ \text{ 6. }f(x)\text{ 在 }{x}_0\text{ 连续 }❌\\ \text{ 7. }f(x)\text{ 在 }{x}_0\text{ 极限存在 }❌\\ \text{ 8. }f(x)\text{ 在 }{x}_0\text{ 有定义 }❌\end{array}$$

四、命题不成立的反例

• $f(x)\text{ 在 }{x}_0\text{ 连续 }\nRightarrow f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }$
  $$\begin{array}{rl}& f(x)=\{\begin{array}{l}x,\text{ 当 }x\text{ 为有理数; }\\ 0,\text{ 当 }x\text{ 为无理数. }\end{array}=x\cdot D(x),\\ & 其中D(x)为狄利克雷函数:D(x)=\{\begin{array}{l}1,x\text{ 为有理数; }\\ 0,x\text{ 为无理数. }\end{array}\\ & \underset{x\to 0}{\lim }f(x)=\underset{x\to 0}{\lim }[xD(x)]=0=f(0),从而f(x)在x=0处连续.\\ & 但如果在x_0\ne 0处,选择不同的路径:\\ & (1)x\to x_0时选择有理数路径,则\underset{x\to x_0}{\lim }f(x)=x_0,\\ & (2)x\to x_0时选择无理数路径,则\underset{x\to x_0}{\lim }f(x)=0.\\ & 所以\underset{x\to x_0}{\lim }f(x)不存在,从而f(x)在x_0\ne 0处不连续.\end{array}$$

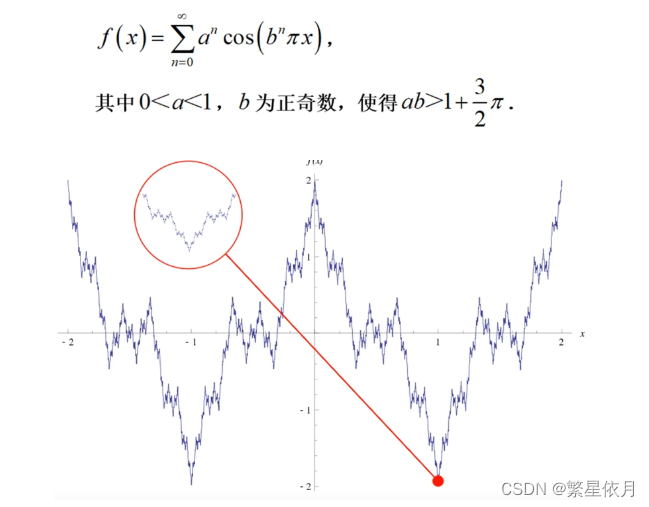
• $f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }\nRightarrow f(x)\text{ 在 }{x}_0\text{ 可导 }$

  处处连续但处处不可导：维尔斯特拉斯函数

  

• 可导是光滑的充分不必要条件

  处处光滑不一定处处可导

  

• $f(x)\text{ 在 }{x}_0\text{ 可导 }\nRightarrow f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }$

  一点可导推不出邻域内连续。
  $$\begin{array}{rl}& f(x)=\{\begin{array}{l}{x}^2,x\text{ 为有理数 }\\ 0,x\text{ 为无理数}\end{array}=x^2\cdot D(x)，\\ & 其中D(x)为狄利克雷函数:D(x)=\{\begin{array}{l}1,x\text{ 为有理数 }\\ 0,x\text{ 为无理数 }\end{array}\\ & f^{\prime }(0)=\underset{x\to 0}{\lim }\frac{f(x)-f(0)}{x-0}=\underset{x\to 0}{\lim }\frac{x^{2}D(x)}{x}=\underset{x\to 0}{\lim }[xD(x)]=0.\\ & \underset{x\to 0}{\lim }f(x)=\underset{x\to 0}{\lim }\left[x^{2}D(x)\right]=0=f(0)，从而f(x)在x=0连续。\\ & 但在其他点，均为间断点，不连续。\end{array}$$

• $f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内可导 }\nRightarrow f^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }$

  $f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内可导 }\nRightarrow f^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内极限存在 }$

  邻域内处处可导，但导函数不连续，极限不存在。
  $$\begin{array}{rl}& f(x)=\{\begin{array}{c}{x}^2\sin \frac{1}{x},x\ne 0\\ 0,x=0\end{array}，f(x)在R上处处可导，但f^{\prime }(x)不连续，有振荡间断点。\\ & f^{\prime }(0)=\underset{x\to 0}{\lim }\frac{f(x)-f(0)}{x-0}=\underset{x\to 0}{\lim }\frac{x^2\sin \frac{1}{x}}{x}=\underset{x\to 0}{\lim }x\sin \frac{1}{x}=0\\ & x\ne 0时，f^{\prime }(x)=2x\sin \frac{1}{x}-\cos \frac{1}{x}，所以f^{\prime }(x)=\{\begin{array}{l}2x\sin \frac{1}{x}-\cos \frac{1}{x},x\ne 0\\ 0,x=0\end{array}\\ & 但\underset{x\to 0}{\lim }{f}^{\prime }(x)=\underset{x\to 0}{\lim }\left(2x\sin \frac{1}{x}-\cos \frac{1}{x}\right)不存在，从而f^{\prime }(x)在x=0处不连续。\end{array}$$

五、概念判断练习

如果 $f(x)$ 在 $x_0$ 二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。❌

2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。❌

3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。✅

4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。❌

5. $f^{\prime }(x)$ 在 $x_0$ 可导。✅

6. $f^{\prime }(x)$ 在 $x_0$ 连续。✅

7. $f^{\prime }(x)$ 在 $x_0$ 有定义。✅

8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。✅

9. $f(x)$ 在 $x_0$ 可导。✅

10. $f(x)$ 在 $x_0$ 连续。✅

11. $f(x)$ 在 $x_0$ 有定义。✅

12. $\underset{x\to x_0}{\lim }f(x)$ 存在。✅

13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。❌

14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。❌

15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。❌

16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。❌

17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。❌

18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。❌

19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。✅

20. $\underset{x\to t}{\lim }{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。❌

21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。✅

22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。✅

23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。✅

24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。✅

如果 $f(x)$ 在 $x_0$ 的邻域 $U_{\delta }(x_0)$ 内二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。❌
2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。❌
3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。✅
4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。❌
5. $f^{\prime }(x)$ 在 $x_0$ 可导。✅
6. $f^{\prime }(x)$ 在 $x_0$ 连续。✅
7. $f^{\prime }(x)$ 在 $x_0$ 有定义。✅
8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。✅
9. $f(x)$ 在 $x_0$ 可导。✅
10. $f(x)$ 在 $x_0$ 连续。✅
11. $f(x)$ 在 $x_0$ 有定义。✅
12. $\underset{x\to x_0}{\lim }f(x)$ 存在。✅
13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。❌
14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。❌
15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。✅
16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。❌
17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。✅
18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。✅
19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。✅
20. ${\lim }_{x\to t}{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。✅
21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。✅
22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。✅
23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。✅
24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。✅

如果 $f(x)$ 在 $x_0$ 的去心邻域 $U_{\delta }(x_0)$ 内二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。❌

2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。❌

3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。❌

4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。❌

5. $f^{\prime }(x)$ 在 $x_0$ 可导。❌

6. $f^{\prime }(x)$ 在 $x_0$ 连续。❌

7. $f^{\prime }(x)$ 在 $x_0$ 有定义。❌

8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。❌

9. $f(x)$ 在 $x_0$ 可导。❌

10. $f(x)$ 在 $x_0$ 连续。❌

11. $f(x)$ 在 $x_0$ 有定义。❌

12. $\underset{x\to x_0}{\lim }f(x)$ 存在。❌

13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。❌

14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。❌

15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。✅

16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。❌

17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。✅

18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。✅

19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。✅

20. $\underset{x\to t}{\lim }{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。✅

21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。✅

22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。✅

23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。✅

24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。✅

如果 $f(x)$ 在 $x=x_0$ 处存在一阶连续导数，判断以下命题是否正确。

1. $f(x)$ 在 $x_0$ 处可导。✅
2. $f(x)$ 在 $x_0$ 的去心邻域内可导。✅
3. $f^{\prime }(x)$ 在 $x_0$ 处连续。✅
4. $f^{\prime }(x)$ 在 $x_0$ 的去心邻域内连续。

如果 $f(x)$ 在 $x=x_0$ 处存在二阶导数，判断以下命题是否正确。

1. $f(x)$ 在 $x_0$ 处可导。✅
2. $f(x)$ 在 $x_0$ 的去心邻域内可导。✅
3. $f^{\prime }(x)$ 在 $x_0$ 处连续。✅
4. $f^{\prime }(x)$ 在 $x_0$ 的去心邻域内连续。❌
5. $f(x)$ 在 $x_0$ 的去心邻域内存在二阶导数。❌

六、无答案练习纯享版

$f(x)$ 在某点连续，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 连续 }\Rightarrow \{\begin{array}{l}\text{ 1. }f(x)\text{ 在 }{x}_0\text{ 邻域内有定义 }\\ \text{ 2. }\underset{x\to x_0}{\lim }f(x)=f\left(x_0\right)\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 可导 }\end{array}$$

$f(x)$ 在某邻域内连续，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }\Rightarrow \{\begin{array}{l}1.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 邻域内有定义 }\\ 2.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 邻域内处处连续 }\\ 3.f(x)\text{ 在 }{x}_0\text{ 可导 }\end{array}$$

$f(x)$ 在某去心邻域内连续，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内连续 }\Rightarrow \{\begin{array}{l}\text{ 1. }f(x)\text{ 在去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }\\ \text{ 2. }f(x)\text{ 在去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内处处连续 }\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 极限存在 }\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 可导 }\end{array}$$

$f(x)$ 在某点可导，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 可导 }\Rightarrow \{\begin{array}{l}\text{ 1. }{f}^{\prime }(x)\text{ 在 }{x}_0\text{ 有定义 }\\ \text{ 2. }{f}_{-}^{\prime }(x)=f_{+}^{\prime }(x)\\ \text{ 3. }f(x)\text{ 在 }{x}_0\text{ 连续 }\\ \text{ 4. }f(x)\text{ 在 }{x}_0\text{ 邻域内连续 }\\ \text{ 5. }f(x)\text{ 在 }{x}_0\text{ 邻域内可导 }\end{array}$$

$f(x)$ 在某邻域内可导，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 某邻域 }{U}_{\delta }\left(x_0\right)\text{ 内可导 }\Rightarrow \{\begin{array}{l}1.f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }\\ \text{ 2. }f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内极限存在 }\\ \text{ 3. }f(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内有定义 }\\ \text{ 4. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内连续 }\\ \text{ 5. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内极限存在 }\\ \text{ 6. }{f}^{\prime }(x)\text{ 在 }{U}_{\delta }\left(x_0\right)\text{ 内有定义 }\end{array}$$

$f(x)$ 在某去心邻域内可导，判断以下命题是否正确。
$$f(x)\text{ 在 }{x}_0\text{ 去心邻域 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内可导 }\Rightarrow \{\begin{array}{l}\text{ 1. }{f}^{\prime }(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }\\ \text{ 2. }f(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内连续 }\\ \text{ 3. }f(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内极限存在 }\\ \text{ 4. }{f}^{\prime }(x)\text{ 在 }{\stackrel{\circ }{U}}_{\delta }\left(x_0\right)\text{ 内有定义 }\\ \text{ 5. }f(x)\text{ 在 }{x}_0\text{ 有定义 }\\ \text{ 6. }f(x)\text{ 在 }{x}_0\text{ 连续 }\\ \text{ 7. }f(x)\text{ 在 }{x}_0\text{ 极限存在 }\\ \text{ 8. }f(x)\text{ 在 }{x}_0\text{ 有定义 }\end{array}$$

如果 $f(x)$ 在 $x_0$ 二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。

2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。

3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。

4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。

5. $f^{\prime }(x)$ 在 $x_0$ 可导。

6. $f^{\prime }(x)$ 在 $x_0$ 连续。

7. $f^{\prime }(x)$ 在 $x_0$ 有定义。

8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。

9. $f(x)$ 在 $x_0$ 可导。

10. $f(x)$ 在 $x_0$ 连续。

11. $f(x)$ 在 $x_0$ 有定义。

12. $\underset{x\to x_0}{\lim }f(x)$ 存在。

13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。

16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。

17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。

20. ${\lim }_{x\to t}{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。

21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。

24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。

如果 $f(x)$ 在 $x_0$ 的邻域 $U_{\delta }(x_0)$ 内二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。
2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。
3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。
4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。
5. $f^{\prime }(x)$ 在 $x_0$ 可导。
6. $f^{\prime }(x)$ 在 $x_0$ 连续。
7. $f^{\prime }(x)$ 在 $x_0$ 有定义。
8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。
9. $f(x)$ 在 $x_0$ 可导。
10. $f(x)$ 在 $x_0$ 连续。
11. $f(x)$ 在 $x_0$ 有定义。
12. $\underset{x\to x_0}{\lim }f(x)$ 存在。
13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。
14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。
15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。
16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。
17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。
18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。
19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。
20. ${\lim }_{x\to t}{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。
21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。
22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。
23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。
24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。

如果 $f(x)$ 在 $x_0$ 的去心邻域 $U_{\delta }(x_0)$ 内二阶可导，判断以下命题是否正确。

1. $f^{\prime \prime }(x)$ 在 $x_0$ 可导。

2. $f^{\prime \prime }(x)$ 在 $x_0$ 连续。

3. $f^{\prime \prime }(x)$ 在 $x_0$ 有定义。

4. $\underset{x\to x_0}{\lim }{f}^{\prime \prime }(x)$ 存在。

5. $f^{\prime }(x)$ 在 $x_0$ 可导。

6. $f^{\prime }(x)$ 在 $x_0$ 连续。

7. $f^{\prime }(x)$ 在 $x_0$ 有定义。

8. $\underset{x\to x_0}{\lim }{f}^{\prime }(x)$ 存在。

9. $f(x)$ 在 $x_0$ 可导。

10. $f(x)$ 在 $x_0$ 连续。

11. $f(x)$ 在 $x_0$ 有定义。

12. $\underset{x\to x_0}{\lim }f(x)$ 存在。

13. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

14. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

15. $f^{\prime \prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。

16. $\underset{x\to t}{\lim }{f}^{\prime \prime }(x)$ 存在, $t\in U_{\delta }\left(x_0\right)$。

17. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

18. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

19. $f^{\prime }(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内有定义。

20. $\underset{x\to t}{\lim }{f}^{\prime }(x)$ 存在, $t\in U_s\left(x_0\right)$。

21. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内可导。

22. $f(x)$ 在 $x_0$ 邻域 $U_{\delta }\left(x_0\right)$ 内连续。

23. $f(x)$ 在 $x_0$ 邻域 $U_s\left(x_0\right)$ 内有定义。

24. $\underset{x\to t}{\lim }f(x)$ 存在，$t\in U_{\delta }(x)$ 。

如果 $f(x)$ 在 $x=x_0$ 处存在一阶连续导数，判断以下命题是否正确。

1. $f(x)$ 在 $x_0$ 处可导。
2. $f(x)$ 在 $x_0$ 的去心邻域内可导。
3. $f^{\prime }(x)$ 在 $x_0$ 处连续。
4. $f^{\prime }(x)$ 在 $x_0$ 的去心邻域内连续。

如果 $f(x)$ 在 $x=x_0$ 处存在二阶导数，判断以下命题是否正确。

1. $f(x)$ 在 $x_0$ 处可导。
2. $f(x)$ 在 $x_0$ 的去心邻域内可导。
3. $f^{\prime }(x)$ 在 $x_0$ 处连续。
4. $f^{\prime }(x)$ 在 $x_0$ 的去心邻域内连续。
5. $f(x)$ 在 $x_0$ 的去心邻域内存在二阶导数。

七、附图

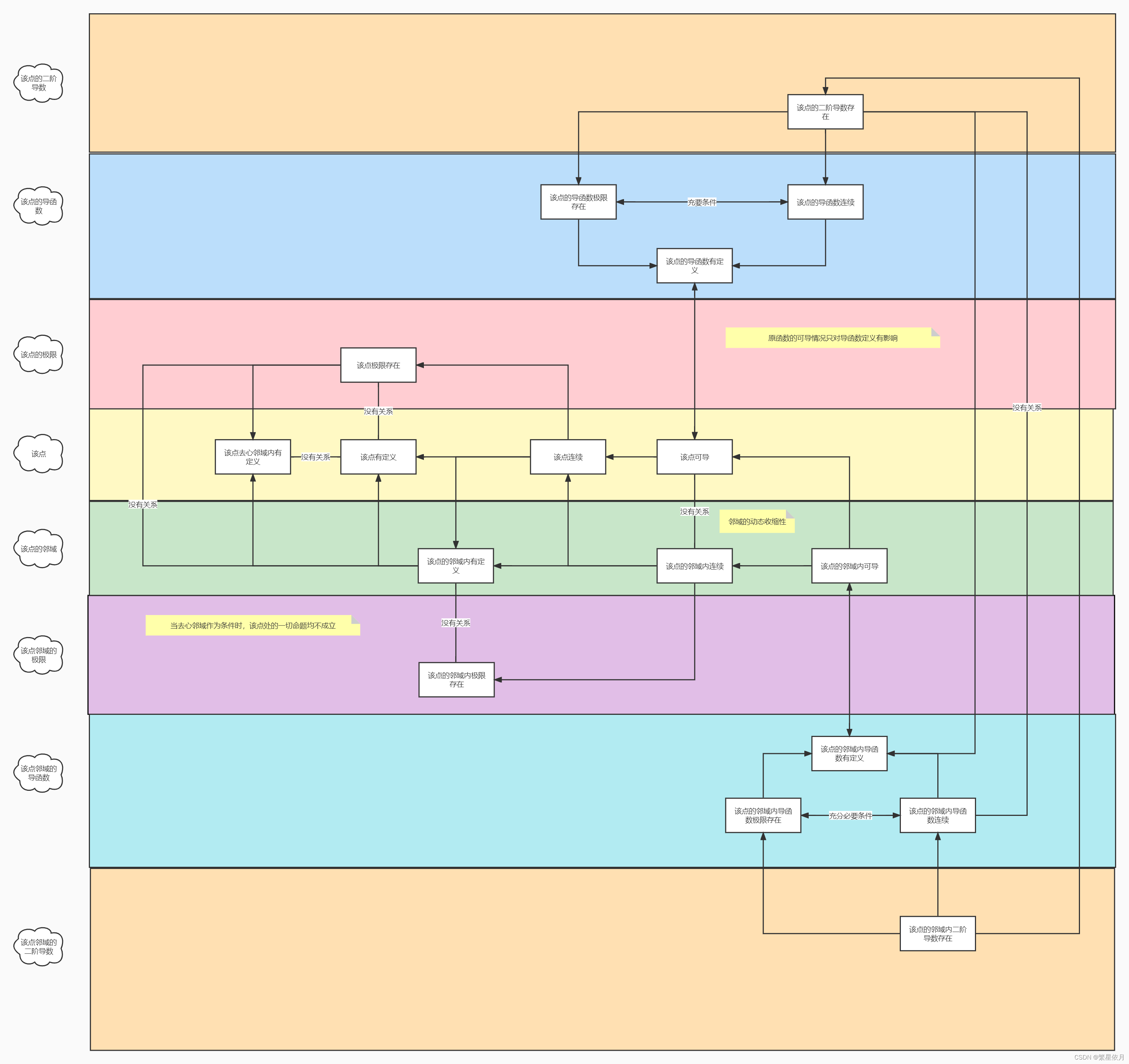
最后

😊为防止河蟹，链接已经通过“与熊论道/熊曰加密”加密处理，将下面的文字复制到“与熊论道/熊曰加密”页面的第二个输入框，点击“领悟熊所言的真谛”即可查看链接啦：
😊熊曰：呋食食擊嗷嘍冬嗚家吃呱山萌萌笨有哞魚既魚性蜜覺呆食哮性洞哮山噗眠嗥嚄萌洞擊嗄襲呱物人你
😊如果嫌麻烦的话请私信咨询博主，谢谢！
😊PS：繁星依月/惟欢/一舟均为博主的马甲，本篇作品完全原创，再次感谢！