高等数学笔记：中值定理【王下七武海】_武忠祥介值定理-优快云博客

本文链接：https://blog.youkuaiyun.com/Ding_Yifan/article/details/124363046

本文详细阐述了微积分中的几个核心中值定理，包括介值定理、零点定理、罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理。这些定理不仅揭示了函数性质的内在联系，还在求解方程、证明不等式和理解函数行为等方面有着广泛应用。同时，介绍了积分中值定理的第一和第二形式，展示了它们在确定函数平均值和判断单调性上的作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

繁星数学随想录·笔记卷

摘录卷

中值定理【王下七武海】

一、介值定理

表述01
- 若 $\in C[a, b], M, m(M>m)$ 分别是 $f (x)$ 在 $[a, b]$ 的最大值和最小值, 则 $∀μ∈(m,M),∃ξ∈(a,b)\forall \mu \in(m, M), \exists \xi \in(a, b)$ 使得 $f(ξ)=μf(\xi)=\mu$
表述02（武忠祥）
- 设 $f (x)$ 在闭区间 $[a, b]$ 上连续，且 $\neq f(b)$ ，则对于任意介于 $f (a)$ 与 $f (b)$ 之间的数 $C$ ，至少存在一点 $ξ∈(a,b)\xi \in (a,b)$ ，使 $f(ξ)=Cf(\xi)=C$

二、零点定理

表述01
- 若 $\in C[a, b], f(a) f(b)<0$ , 则 $∃ξ∈(a,b)\exists \xi \in(a, b)$ , 使得 $f(ξ)=0f(\xi)=0$
表述02（武忠祥）
- 设 $f (x)$ 在闭区间 $[a, b]$ 上连续，且 $f (a) \cdot f (b) < 0$ ，则至少存在一点 $ξ∈(a,b)\xi\in(a,b)$ ，使 $f(ξ)=0f(\xi)=0$

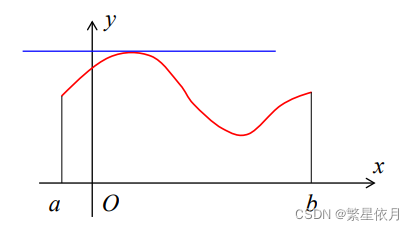
三、罗尔定理

罗尔定理
- 若 $f (x)$ 满足：
  (1) $f(x)∈C[a,b]f(x)\in C[a,b]$ ——区间上连续
  (2) $f(x)∈D[a,b]f(x)\in D[a,b]$ ——区间内可导
  (3) $f (a) = f (b)$ ——端点函数值相等
  则至少存在一点 $ξ∈(a,b)\xi \in (a,b)$ ，使 $f’(ξ)=0f^{’}(\xi)=0$
几何解释

四、拉格朗日中值定理

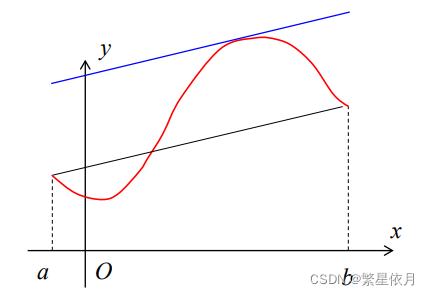
拉格朗日中值定理
- 若 $f (x)$ 满足：
  
  (1) $f(x)∈C[a,b]f(x)\in C[a,b]$ ——区间上连续
  
  (2) $f(x)∈D(a,b)f(x)\in D(a,b)$ ——区间内可导
  
  则至少存在一点 $ξ∈(a,b)\xi \in (a,b)$ ，使 $f’(ξ)=f(b)−f(a)b−af^{’}(\xi)=\frac{f(b)-f(a)}{b-a}$ 或 $f′(ξ)(b−a)=f(b)−f(a)f'(\xi)(b-a)=f(b)-f(a)$
几何解释
定理的另一种形式
- 函数的有限增量公式
- $θ∈(0,1)\exists \, \theta \in(0,1)$ ， $f(x+Δx)−f(x)=f′(x+θΔx)Δxf(x+\Delta x)-f(x)=f^{\prime}(x+\theta \Delta x) \Delta x$
推论
- (1) $(x∈I)f^{\prime}(x) \equiv 0 \, (x \in I) \Rightarrow f(x) \equiv c \, (x \in I)$
- (2) $(x∈I)f^{\prime}(x) \equiv k \, (x \in I) \Rightarrow f(x)=kx+b \, (x \in I)$
- (3) 导数极限定理：函数在 $U(x_0)$ 上连续，在 $U∘(x0)\stackrel{\circ}{U}(x_0)$ 内可导，且 $lim⁡x→x0f′(x0)\lim \limits_{x \rightarrow x_0}f'(x_0)$ 存在，则 $f (x)$ 在点 $x_0$ 处可导，且 $f′(x0)=lim⁡x→x0f(x0)f'(x_0)=\lim \limits_{x \rightarrow x_0}f(x_0)$
说明
- 拉格朗日中值定理是罗尔定理的推广。
- 定理可证方程开区间内有根。
- 定理可证不等式（不等式中出现函数增量）。

五、柯西中值定理

柯西中值定理
- 若 $f (x)$ 满足：
  
  (1) $f(x)∈C[a,b]f(x)\in C[a,b]$ ——区间上连续
  
  (2) $f(x)∈D[a,b]f(x)\in D[a,b]$ ——区间内可导，且 $\neq 0$
  
  则至少存在一点 $ξ∈(a,b)\xi \in (a,b)$ ，使 $f′(ξ)g′(ξ)=f(b)−f(a)g(b)−g(a)\frac{f^{\prime}(\xi)}{g^{\prime}(\xi)}=\frac{f(b)-f(a)}{g(b)-g(a)}$ .
柯西中值定理是拉格朗日中值定理的推广，当 $g (x) = x$ 时，形式同拉格朗日中值定理。
定理可证方程有根（出现两个函数增量）。

六、泰勒中值定理

01 一点附近的泰勒公式

一点附近的泰勒公式
- $f (x)$ 在 $x_{0}$ 附近定义, 且在 $x_{0}$ 有 $n$ 阶导数，则
  
  $f(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2!(x−x0)2+⋯+f(n)(x0)n!(x−x0)n+o((x−x0)n)f(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\cdots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+o\left(\left(x-x_{0}\right)^{n}\right)$
  
  $o((x−x0)n)o\left(\left(x-x_{0}\right)^{n}\right)$ ——皮亚诺余项
注意：条件相当弱，只要在 $x_0$ 一点有 $n$ 阶导数即可

02 区间 $(a, b)$ 上的泰勒公式

区间 $(a, b)$ 上的泰勒公式
- $f (x)$ 在 $(a, b)$ 有 $n + 1$ 阶导数, $x0∈(a,b)x_{0} \in(a, b)$ , 则在 $(a, b)$ 成立，则
  
  $=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\cdots +\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+R_{n}(x)$
  
  其中， $Rn(x)=f(n+1)(ξ)(n+1)!(x−x0)n+1R_{n}(x)=\frac{f^{(n+1)}(\xi)}{(n+1) !}\left(x-x_{0}\right)^{n+1}$ ， $ξ\xi$ 在 $x, x_{0}$ 之间

03 麦克劳林公式

$f(x)=f(0)+f′(0)x+f′′(0)2!x2+⋯+f(n)(0)n!xn+Rn(x)f(x)=f(0)+f^{\prime}(0) x+\frac{f^{\prime \prime}(0)}{2 !} x^{2}+\cdots+\frac{f^{(n)}(0)}{n !} x^{n}+R_{n}(x)$ ，

$Rn(x)=f(n+1)(θx)(n+1)!xn+1(θ∈(0,1))R_{n}(x)=\frac{f^{(n+1)}(\theta x)}{(n+1) !} x^{n+1} \quad(\theta \in(0,1))$ 或 $o(xn)o\left(x^{n}\right)$