基于Matlab的BP神经网络电力系统短期负荷预测研究

摘要：随着电力系统规模的不断扩大和用电负荷的日益波动，准确的短期负荷预测对电网的安全稳定运行及经济调度具有重要意义。传统的时间序列和回归分析方法在处理非线性、强随机性的负荷数据时往往存在精度不足的问题。

作者：Bob(原创)

项目概述

本研究基于 MATLAB，利用 BP 神经网络实现对电力系统短期负荷的日负荷曲线预测。所使用的数据为 2018 年实际电力负荷的逐日 96 点（15 分钟间隔）历史记录，按日期存储于 Excel 文件中。论文首先通过自编函数从指定目录逐日读取负荷数据，提取当日 96 个采样点及对应的最大值、最小值，并采用线性归一化方法将数据映射到 [0,1] 区间。随后，以连续数日的归一化负荷曲线作为神经网络输入，以下一日对应时刻的负荷曲线作为预测目标，构建输入维度为多日负荷、输出维度为 1 日 96 点负荷的前馈 BP 网络。网络采用两层隐含层结构，分别使用 tansig 和 logsig 激活函数，并通过共轭梯度法（traincgf）进行训练。

训练完成后，将神经网络预测输出反归一化，以恢复为实际负荷值，并绘制与真实负荷的对比曲线。实验结果表明，该 BP 神经网络能够在一定程度上反映负荷的日内变化趋势，预测曲线与真实曲线在多数时段保持接近，但在尖峰或谷底时段的拟合精度受到一定影响。总体而言，基于 MATLAB 实现的该 BP 神经网络模型能够完成短期日负荷曲线的预测任务，适用于基础级的负荷预测研究或教学示例。

系统设计

本系统通过 MATLAB 编程实现数据读取、归一化处理、BP 神经网络训练与负荷预测的完整流程。

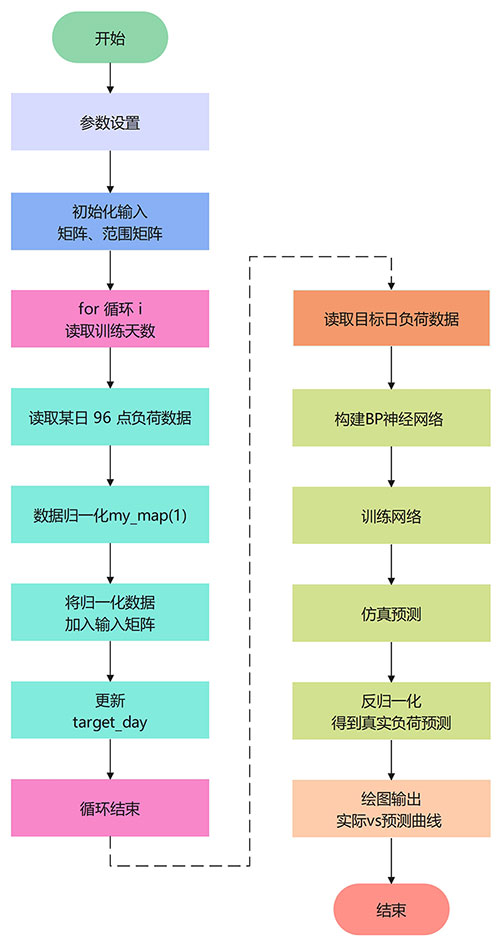
图1 系统整体流程图

硬件配置

该系统硬件配置如上，如果您的电脑配置低于下述规格，运行速度可能会与本系统的存在差异，请注意。

表1 惠普(HP)暗影精灵10台式整机配置(系统硬件配置)

软件环境

对本实验所需的各类软件及工具的基本信息进行了清晰汇总。

表2 系统软件配置(真实运行环境)

运行展示

运行main.m

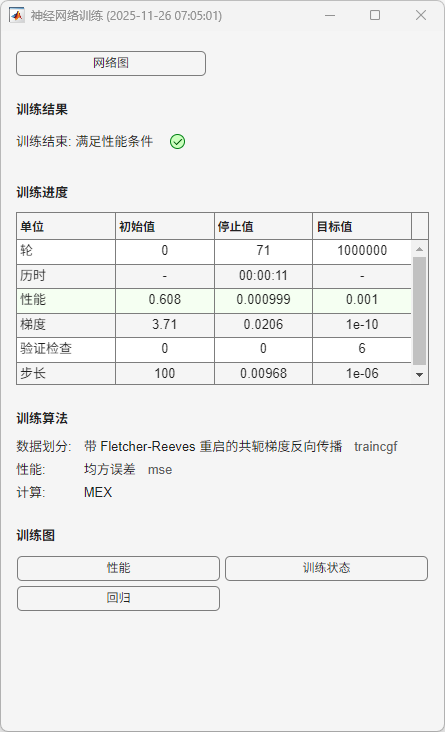
图2 BP 神经网络训练界面及性能达到目标时的状态

该图显示了 BP 神经网络在 MATLAB 神经网络工具箱中的训练过程信息。训练算法为 Fletcher–Reeves 共轭梯度法（traincgf），损失函数为均方误差（MSE）。训练在第 71 轮达到性能目标并自动停止，说明模型已满足设定的误差要求。

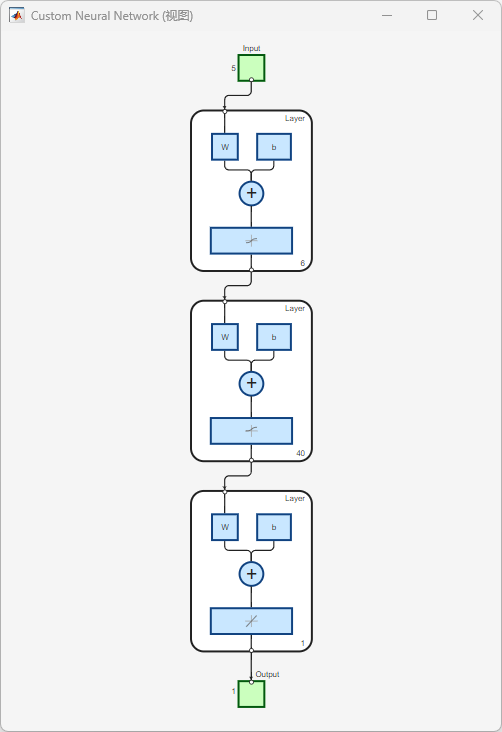
图3 BP 神经网络结构示意图

该图展示了本研究采用的 BP 神经网络模型结构。输入层包含 5 个节点，对应连续 5 天的负荷特征；网络包含两个隐含层，分别为 6 个和 40 个神经元；输出层包含 1 个节点，用于预测目标日相同时间点的负荷值。各层之间采用前馈连接方式。

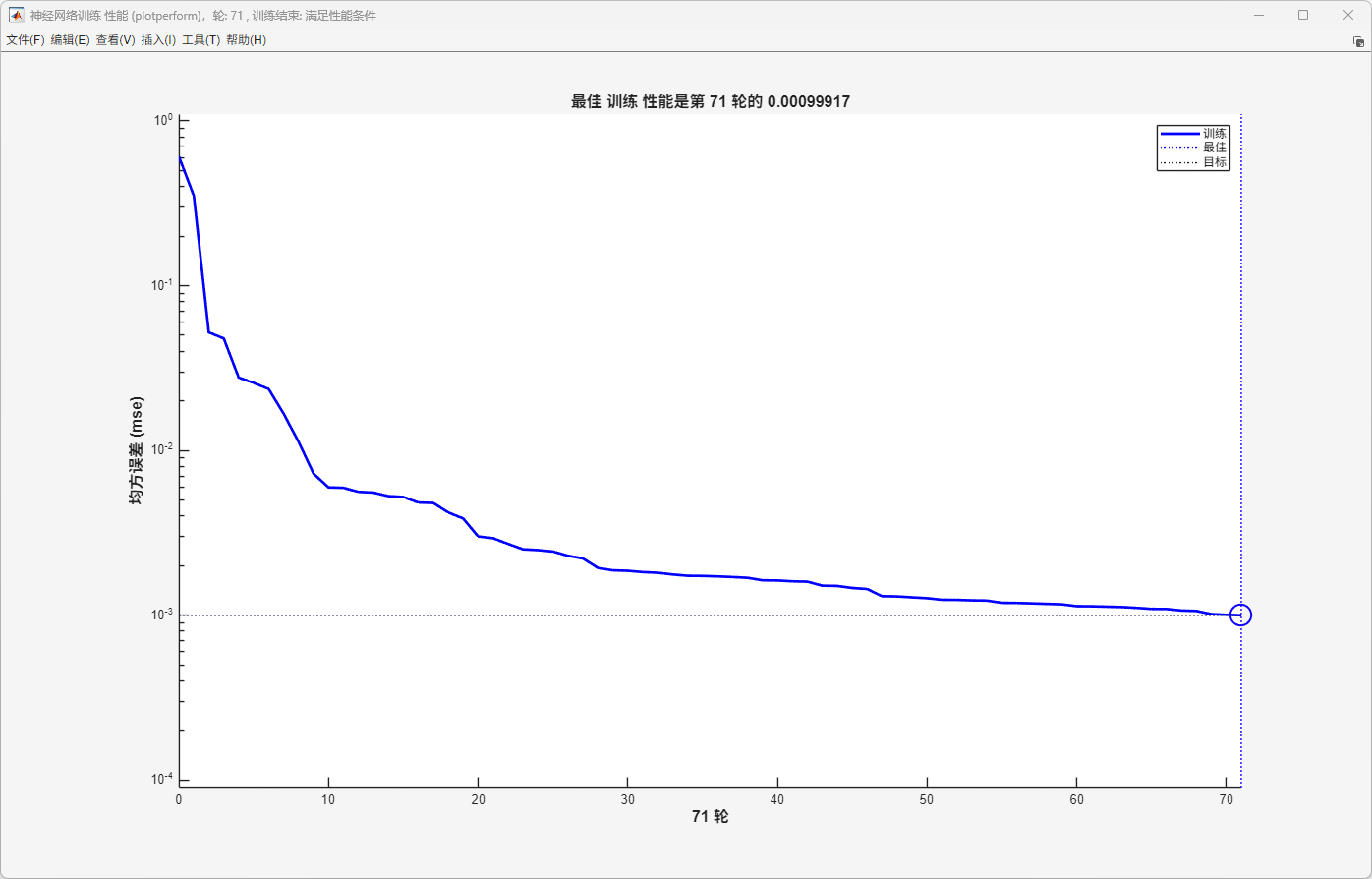
图4 BP 神经网络训练性能曲线（MSE 随训练轮次收敛情况）

该图给出了 BP 神经网络训练过程中均方误差（MSE）随训练轮次的变化情况。随着训练进行，MSE 持续下降并最终收敛至约 0.000999，达到设定的目标误差 0.001。曲线呈明显下降趋势，说明模型学习效果良好。

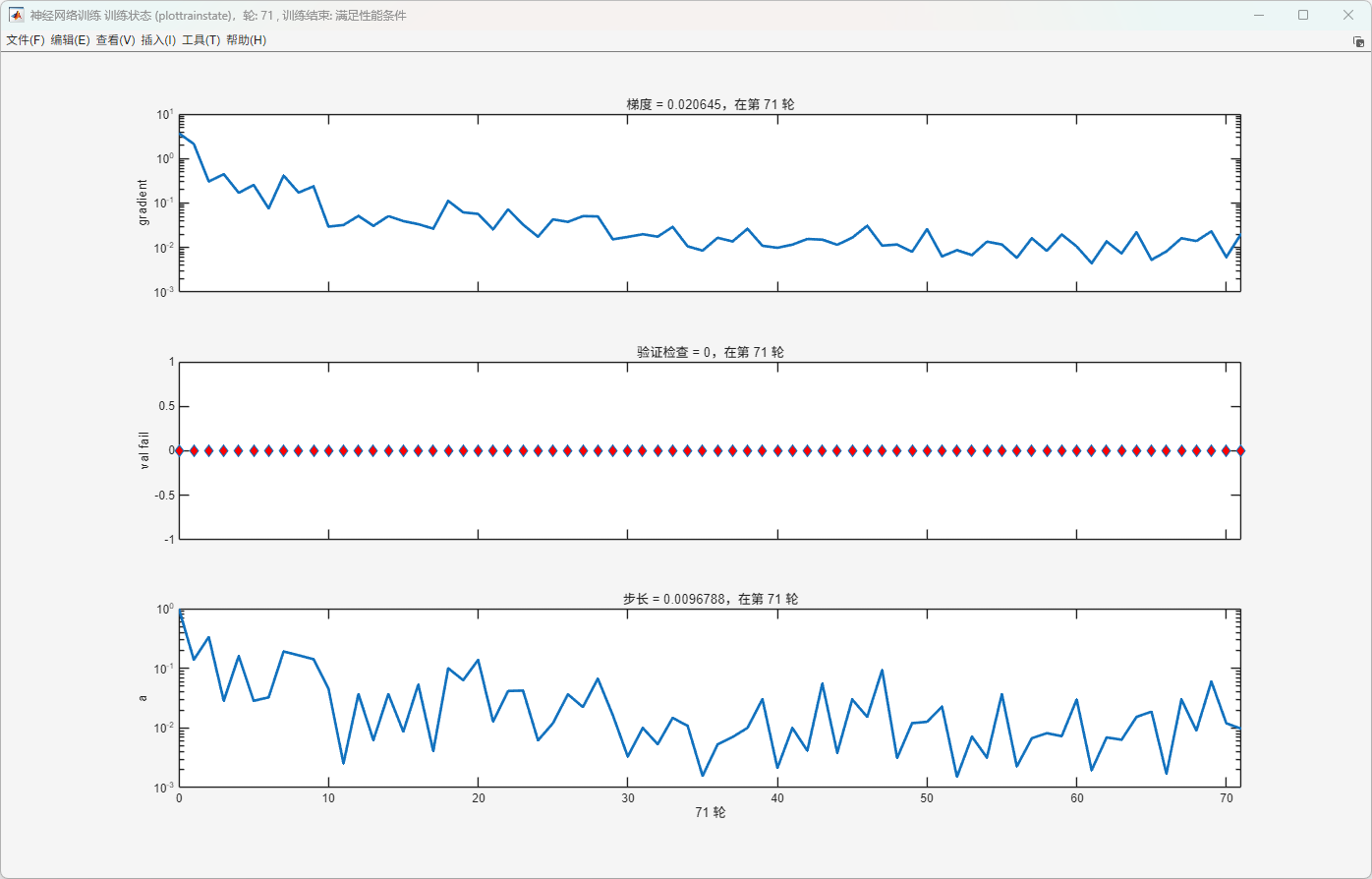
图5 BP 神经网络训练状态曲线（梯度、验证检查与步长）

图中分别显示了训练过程中的梯度、验证检查次数和步长变化情况。梯度整体呈下降趋势，表明网络参数逐步收敛；验证检查次数保持为 0，说明未触发提前停止条件；步长随优化过程动态变化，符合共轭梯度法的特性。
 

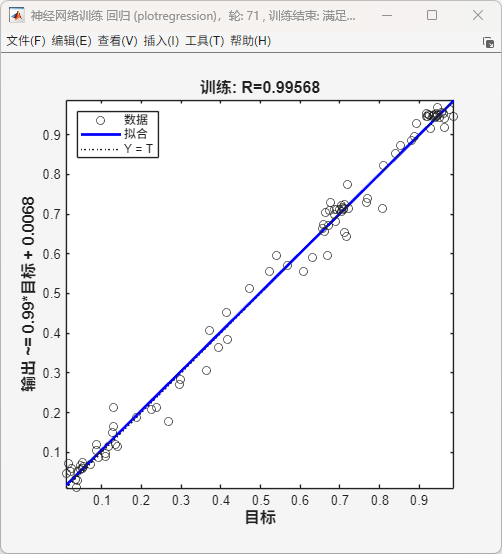
该图展示了网络输出与目标值之间的回归关系。散点为实际训练样本，蓝色直线为拟合线。拟合斜率接近 1 且相关系数 R=0.99568，表明网络输出与真实目标值具有良好一致性，预测精度较高。

图6 BP 神经网络训练回归图（拟合度 R = 0.99568）

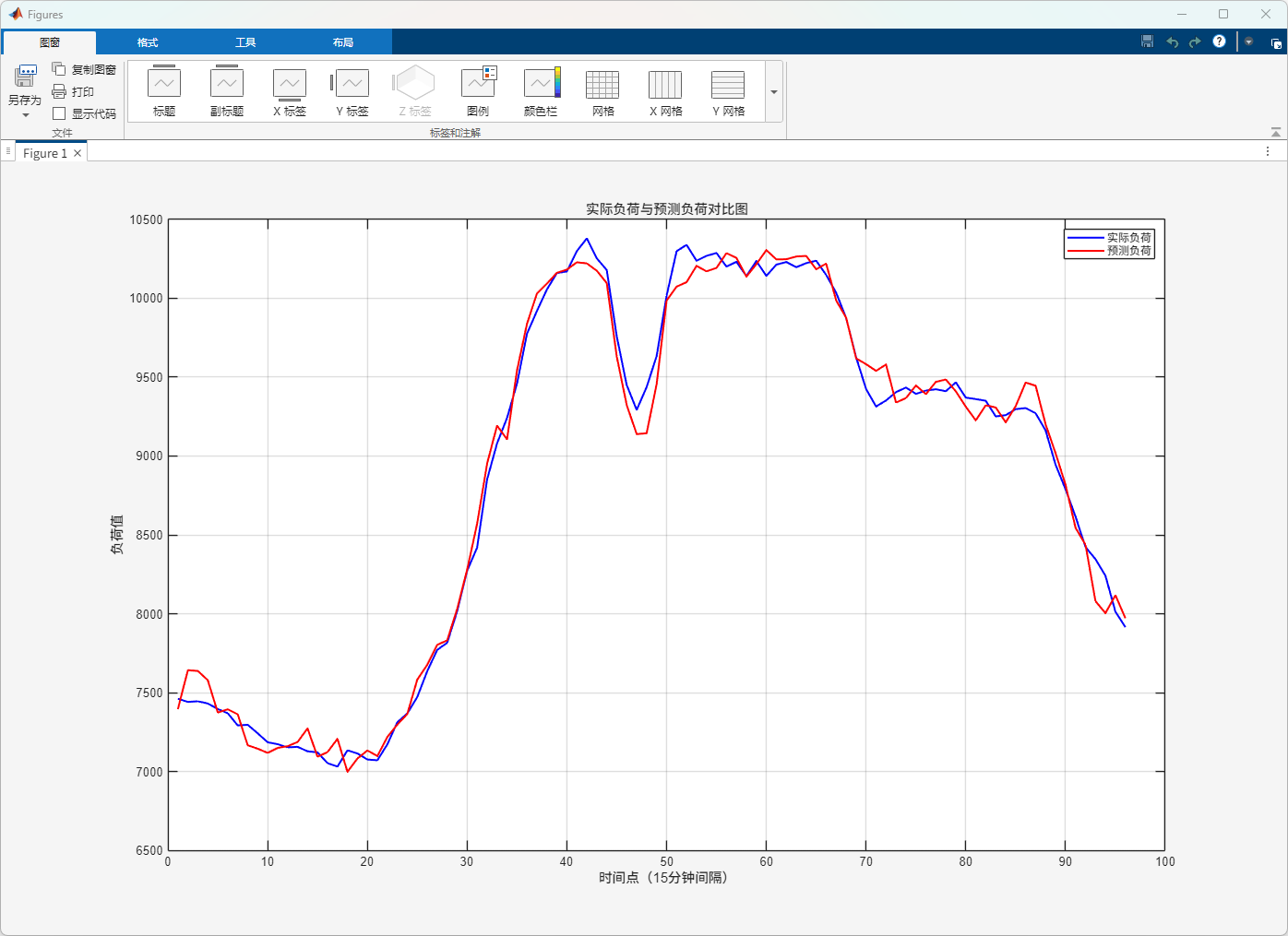
图7 实际负荷与预测负荷对比图

该图对比了 BP 神经网络预测负荷与实际负荷曲线。总体来看，预测曲线较好地跟随了实际负荷的变化趋势，在早晚波动、峰值与谷值附近能够保持较高的拟合度。局部误差主要出现在峰值附近，属于短期负荷预测中的常见现象。