Matlab综合实例：方程组的求解

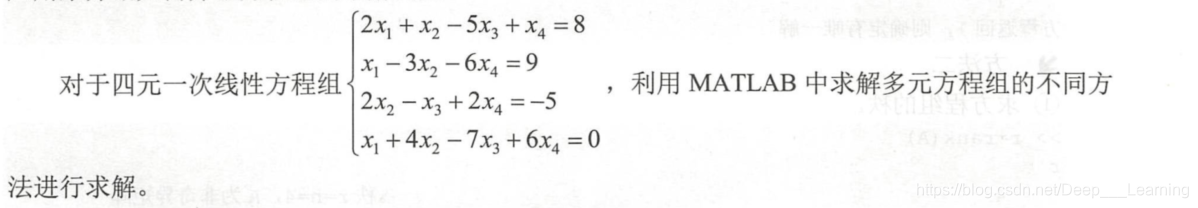
0x01 利用矩阵的逆

1、创建方程组的系数矩阵

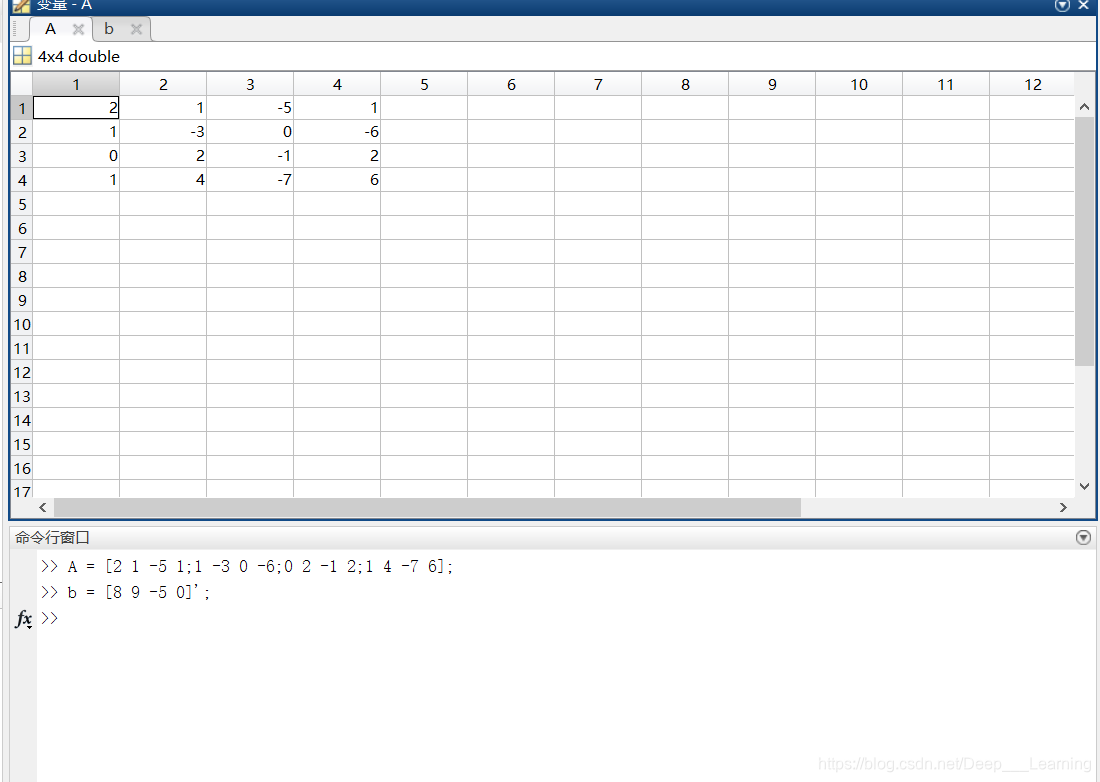
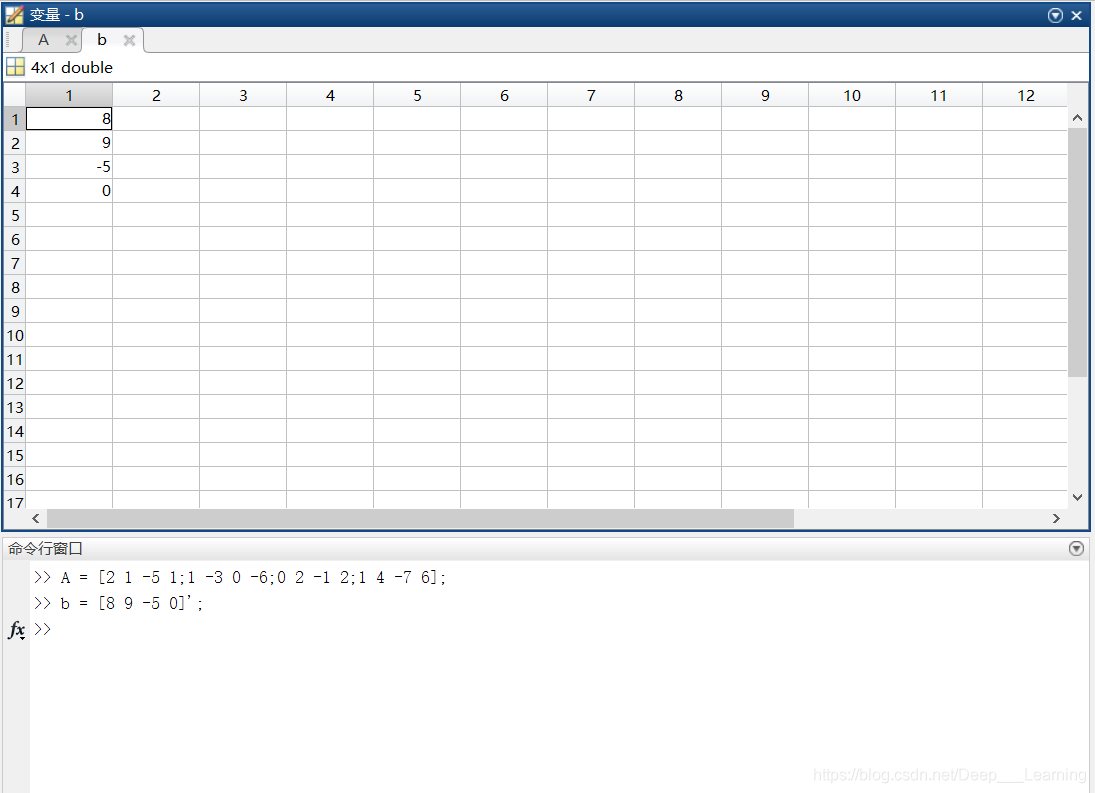
2、判断方程组是否存在解

function y=isexist(A, b)
[m, n] = size(A);
[mb, ~] = size(b);
if m~=mb
    error('输入错误!');
end
r = rank(A);
s = rank([A, b]);
if r==s && r==n
    y=1;
elseif r==s && r < n
    y=Inf;
else
    y=0;
end

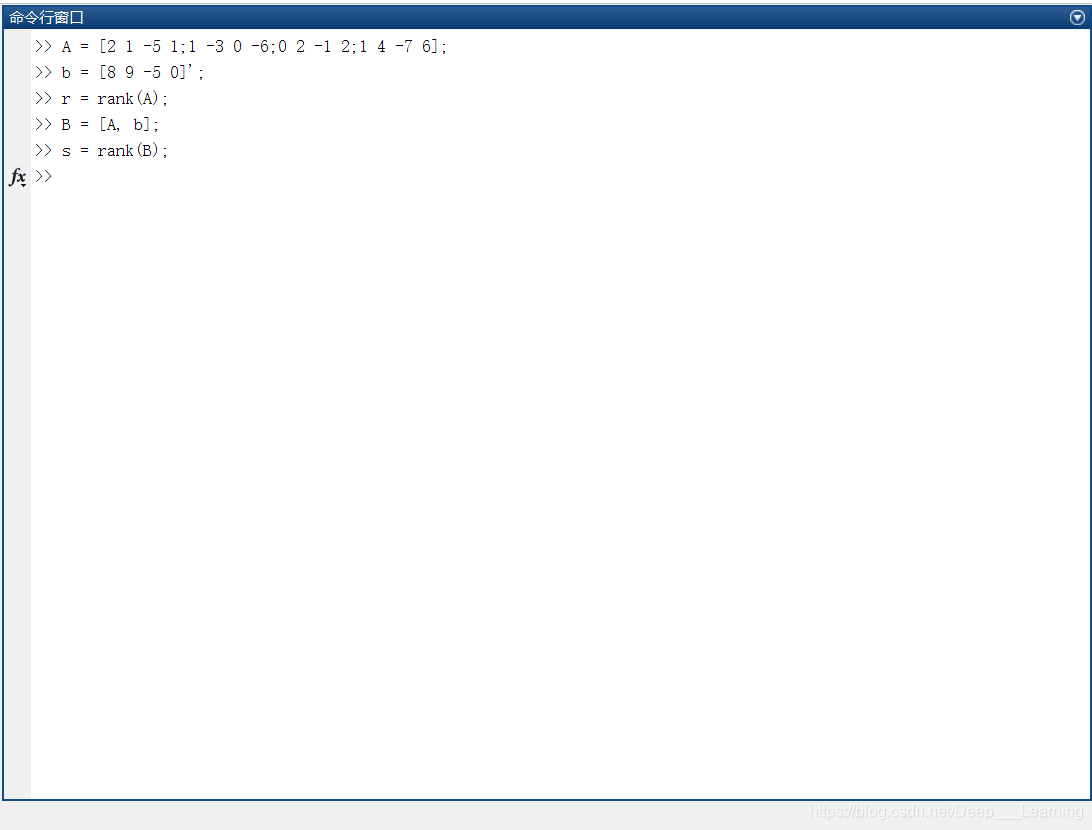
r=s=n=4，该方程组存在唯一的解

3、利用矩阵的逆求解

>> x0 = pinv(A)*b

x0 =

    3.0000
   -4.0000
   -1.0000
    1.0000

>> b0 = A*x0

b0 =

    8.0000
    9.0000
   -5.0000
   -0.0000

0x02 利用矩阵的分解

利用矩阵的分解来求解线性方程组，是工程计算中最常用的技术。

LU分解法

LU分解法是先将系数矩阵A进行LU分解，得到LU=PA，然后解Ly=Pb，最后再解Ux=y得到原方程组的解。

function x = solvebyLU