SLAM后端

1. VSLAM 模块划分与模块功能

VSLAM 是利用多视图几何理论，根据相机拍摄的图像信息对相机进行定位并同时构建周围环境地图。按照相机的分类，有单目、双目、 RGBD、鱼眼、全景等。同时，VSLAM 主要包括视觉里程计（visual odometry， VO）、后端优化、回环检测、建图。
VSLAM 主要包括视觉里程计（visual odometry， VO）、后端优化、回环检测、建图。 其中 VO 研究图像帧间变换关系完成实时的位姿跟踪， 对输入的图像进行处理，计算姿态变化， 得到相机间的运动关系；但是随着时间的累计，误差会累积，这是由于仅仅估计两个图像间的运动造成的，后端主要是使用优化方法，减小整个框架误差（包括相机位姿和空间地图点）。回环检测，又称闭环检测，主要是利用图像间的相似性来判断是否到达过先前的位置，以此来消除累计误差，得到全局一致性轨迹和地图。建图，根据估计的轨迹，建立与任务要求对应的地图。

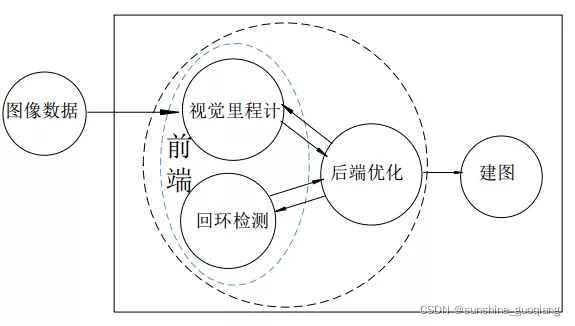
VSLAM 前端为视觉里程计和回环检测，相当于是对图像数据进行关联；
后端是对前端输出的结果进行优化，利用滤波或非线性优化理论，得到最优的位姿估计和全局一致性地图。

现在比较通常的惯例是把 VSLAM 分为前端和后端。前端为视觉里程计和回环检测，相当于是对图像数据进行关联；后端是对前端输出的结果进行优化，利用滤波或非线性优化理论，得到最优的位姿估计和全局一致性地图。

前端的视觉里程计可以给出一个增量式的地图，但由于不可避免的误差累计，这个地图在长时间内是不准确的。而SLAM致力于构建一个长生命周期的可靠的解决方案，因此只有前端是远远不够的。当地图增长到一定程度后，累计误差会使后来的数据越来越不准确。这时我们需要把所有地图数据放到一起做一次完整的优化，从而降低各部分的误差。

2. 后端优化方案

后端优化有很多种方案，过去采用以扩展卡尔曼滤波（Extended Kalman Filter，EKF）为主的滤波器方案，现在大多都采用非线性优化方案。EKF由于假设了马尔可夫性质，只利用前一状态来估计当前状态的值，这有点像视觉里程计中只考虑相邻两帧的关系一样，很难做到全局的优化。而现在常用的非线性优化方法，则是把所有数据都考虑进来，放在一起优化，虽然会增大计算量，但效果好得多。

BA来做非线性优化，但只是优化相邻两张图片间的位姿和路标点。而现在，对于后端优化来说，我们需要优化整个地图的全部位姿和全部路标点，数据量比之前大了不知多少倍。

虽然理论上来说，数据量大并不影响BA方法。但唯一的障碍是数据量大会导致计算时间急剧增大。因为在用梯度下降法求解时，每一轮迭代至少要解一个线性方程组，这就等同于求一个矩阵的逆。矩阵求逆的时间复杂度是O(n3)，于是巨大的数据量导致这个矩阵维度极高，从而使求解用时大的离谱。这也就解释了为什么EKF曾经是后端优化的主流，因为它计算量小呀。

那为什么非线性优化又后来居上了呢？

21世纪以来，人们逐渐意识到如果矩阵具有一定形式的稀疏性，可以加速求逆的过程。而SLAM后端的非线性优化恰恰可以利用这一性质！

SLAM的相机位姿和路标点其实具有非常特殊的结构，并非随机产生。相机位姿和路标点之间是多对多的关系，一个相机位姿可以观测到多个路标点，一个路标点也可以被多个相机位姿观测到。由于相机的大范围运动，局部区域的路标点只会被局部的几个相机位姿观测到，而其它大部分相机位姿都观测不到这些点，这是产生稀疏性的根源。当我们构建了非线性优化的代价函数后，需要求代价函数对所有优化变量的偏导数，稀疏性意味着这些偏导数大部分为0，只有小部分不为0，这些不为0的项对应着相机位姿与其能够观测到的路标点的组合。Schur消元法利用矩阵的稀疏性求逆，是BA中求解增量方程的常用手段。

3. 建图

地图的具体形式主要有路标地图、拓扑地图、度量地图和混合地图。

路标地图，由一堆路标点组成，在早期的基于 EKF 的SLAM 中比较常见。

拓扑地图强调地图元素之间的连通关系，由节点和边组成，只考虑节点间的连通性， 而对精确的位置要求不高，去掉了大量地图的细节，是一种比较紧凑的地图表达方式。

度量地图分为栅格地图和几何地图。栅格地图将整个环境分为若干个大小相同的栅格，每个栅格代表环境的一部分。二维栅格地图在以激光雷达为传感器的扫地机器人里十分常见，它只需用 0-1 表示某个点是否有障碍，对导航很有用，而且精度也比较高， 但是它比较占存储空间，尤其是三维栅格地图，它需要把所有的空间点都存起来。
几何地图通过收集对环境的感知信息，从中提取几何特征（如点、线、面）描述环境， 多见于早期的 SLAM 算法中。

混合地图通常采用分层结构将多种地图组合， 如拓扑地图和度量地图组成的混合地图， 上层的拓扑地图实现粗略的全局路径规划，底层的度量地图实现精确的定位和路径的优化。

在 VSLAM 中广泛应用的是度量地图, 它精确地表示地图中物体的位置关系， 可按稀疏和稠密划分。**特征点法得到稀疏点云地图，直接法得到半稠密或稠密地图。**针对稠密的度量地图， 当查询某个空间位置时，地图能够给出该位置是否可以通过的信息。

VSLAM 中建图的基本原理是通过三角测量或深度估计，将 2D 图像中的信息转换为空间 3D 路标点。在 VSLAM 中建图过程和位姿估计过程是同时完成的。

深度估计在建图模块中占据非常重要的地位， 通常在VSLAM 系统中都有专门的线程对其进行处理。 SVO 采用高斯加上均匀分布的方法估计三维空间点的深度信息，并不断更新，直到其收敛。在 LSDSLAM 中，针对关键帧，通过之前关键帧的点投影初始化当前帧的深度估计；针对非关键帧，通过卡尔曼滤波不断地利用观测值对深度进行修正。

https://www.jianshu.com/p/e4a45ccd128f
https://www.cnblogs.com/bokeyuan-dlam/articles/12667025.html
https://github.com/gaoxiang12/slambook/tree/master/ch10/g2o_custombundle