李群与李代数

通过李群——李代数间的转换关系，我们希望把位姿估计变成无约束的优化问题，简化求解方式。

1. conclusion

李代数的引出：

李代数对应李群的正切空间，它描述了李群局部的导数。
结论0：李代数求导

结论1：李代数求导

对于某个时刻的R(t)（李群空间），存在一个三维向量φ=（φ1，φ2，φ3）（李代数空间），用来描述R在t时刻的局部的导数。

在这里插入图片描述

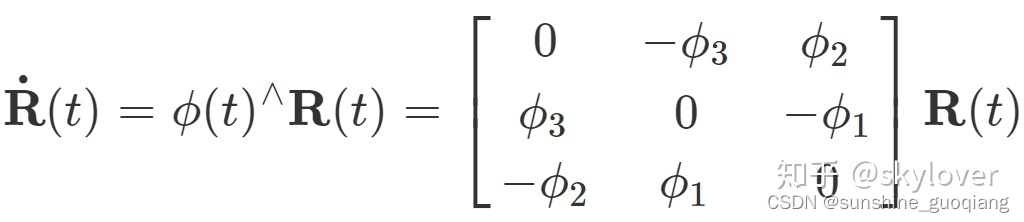
结论2：
R在原点附近的一阶泰勒展开，我们看到这个向量φ=（φ1，φ2，φ3）反应了R的导数性质，故称它在SO(3)上的原点 φ0 附近的正切空间上。这个φ正是李群大SO(3)对应的李代数小so(3)。

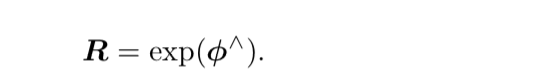
李群空间的任意一个旋转矩阵R都可以用李代数空间的一个向量的反对称矩阵指数来近似。

2. relationship

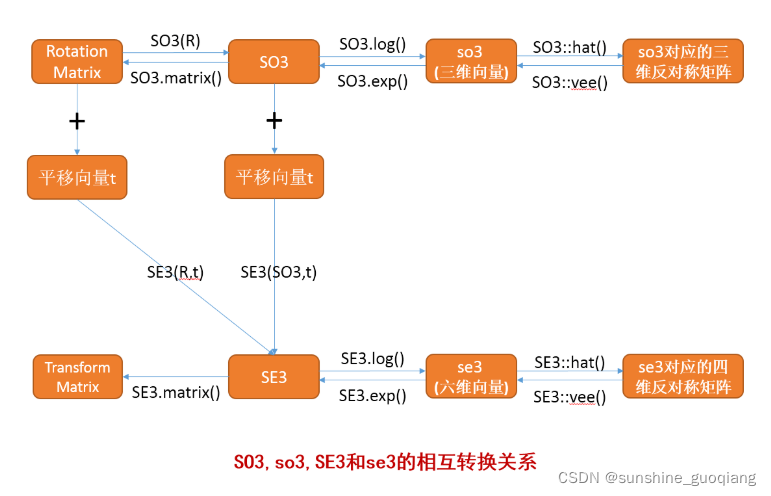
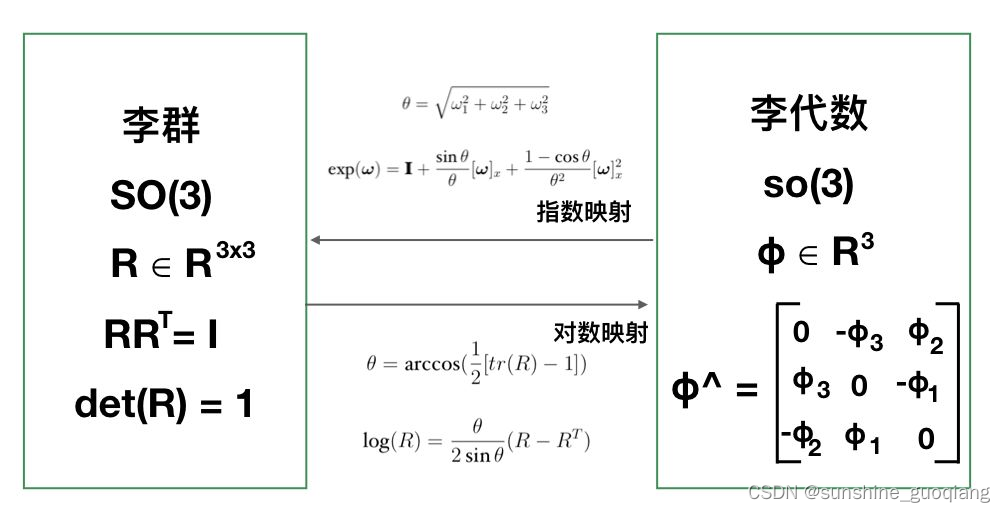
3. SO(3)与so(3)的相互转换

用旋转矩阵表示的话就是李群空间，也是我们熟悉的表示方法。而用向量的反对称矩阵表示的话就是李代数空间，这两个空间建立了联系。

如何计算指数映射呢？进过推导如下：

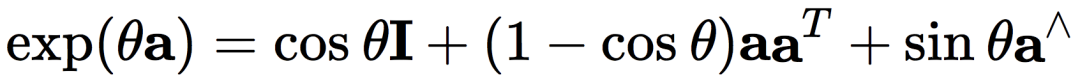
其中：三维向量 φ = θa，a是一个长度为1的方向向量。

这个式子和罗德里格斯公式如出一辙！而罗德里格斯公式是表示从旋转向量到旋转矩阵的转换过程

旋转向量就是这里的李代数，李代数是对加法封闭的

小so(3)的李代数空间就是由旋转向量组成的的空间，其物体意义就是旋转向量。而前面结论二中的指数映射关系就是罗德里格斯公式，他们在数学上本质是一样的

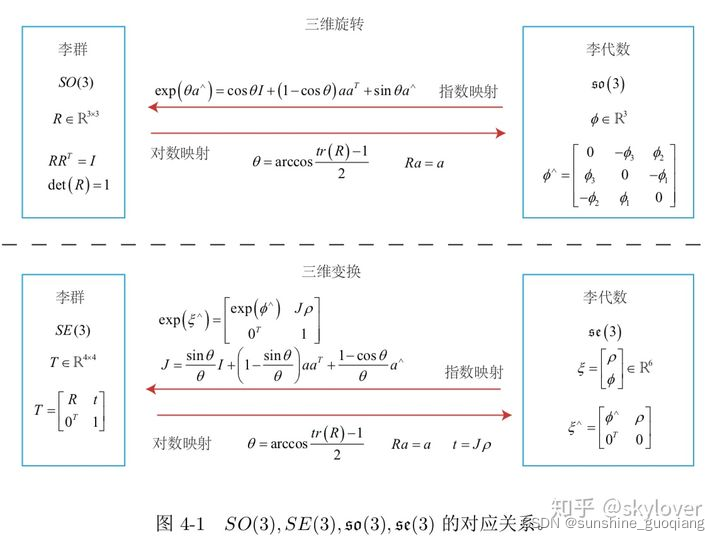
好了，再考虑如下的 ：

比如你拿着相机一边移动一边拍，假设某个时刻相机的位姿是T，它观察到一个在世界坐标系中的一个空间点p，并在相机上产生了一个观测数据z，那么

z = Tp + noise

noise是观测噪声。那么观测误差就是

e = z - Tp

我们的目的就是使得误差最小

假设我们总共有N个这样的三维点p和观测值z，那么我们的目标就是寻找一个最佳的位姿T，使得整体误差最小化，也就是

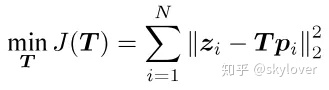
我们先来看看变换矩阵T，我们知道T所在的SE(3)空间，对加法计算并不封闭，也就是说任意两个变换矩阵相加后并不是一个变换矩阵，这主要是因为旋转矩阵对加法是不封闭造成的，它是有约束的。

我们经常会构建与位姿有关的函数，然后讨论该函数关于 位姿的导数，以调整当前的估计值。然而，SO(3), SE(3) 上并没有良好定义的加法，它们 只是群。如果我们把 T 当成一个普通矩阵来处理优化，那就必须对它加以约束。而从李代数角度来说，由于李代数由向量组成，具有良好的加法运算。
李代数就是解决这个问题的。我们把大写SE(3)空间的T映射为一种叫做李代数的东西，映射后的李代数我们叫做小se(3)好了。它是由向量组成的，我们知道向量是对加法封闭的。这样我们就可以通过对李代数求导来间接的对变换矩阵求导了。

李代数是由向量组成的，向量对加法运算是封闭的。

李代数求导分两种：一种是用李代数表示位姿，然后根据李代数加法来对李代数求导，结果中有复杂的雅克比公式，不是很方便。一般都用第二种，就是对李群进行左乘或者右乘微小的扰动，然后对该扰动求导，如下：

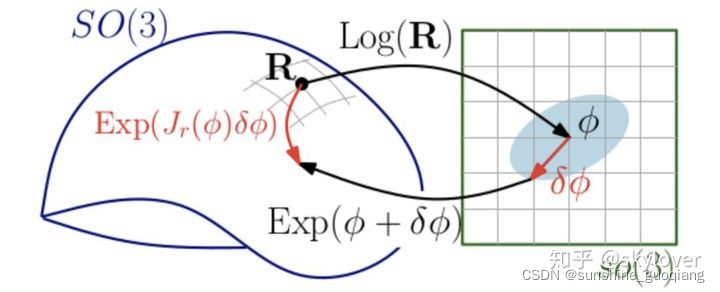
c++中关乎李代数的是Sophus库

https://www.icxbk.com/article/detail/1313.html
https://zhuanlan.zhihu.com/p/87802961
https://zhuanlan.zhihu.com/p/75366449