191025-主席树

最新推荐文章于 2020-07-27 21:18:18 发布

原创最新推荐文章于 2020-07-27 21:18:18 发布 · 201 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#主席树

数据结构专栏收录该内容

23 篇文章

订阅专栏

191025-主席树

定义

在讲主席树之前，先讲讲权值线段树：
何为权值线段树呢？
权值线段树定义
接下来再讲主席树：
**主席树的本质就是一棵棵权值线段树，或者说是一个权值线段树的前缀和。**或许有点难理解，来看下面一个问题。

问题引入（传送门）

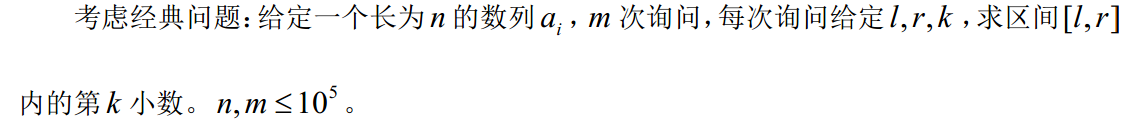
求解

1，首先面对求第k小数，我们就可以考虑二分答案，详解如下；
step1
2，一种方法是每次将询问区间排序，然后二分求解，但由于有多次询问，时间复杂度必爆。因此我们考虑维护主席树，详解如下：
step2
3，我们分别查询第r棵权值线段树的 $[1, a n s]$ 这个区间内数的个数 $c n t 1$ ，以及第l-1棵权值线段树的 $[1, a n s]$ 这个区间内数的个数 $c n t 2$ ，则 $c n t 1 - c n t 2$ 就是我们所求的答案.分析如下：
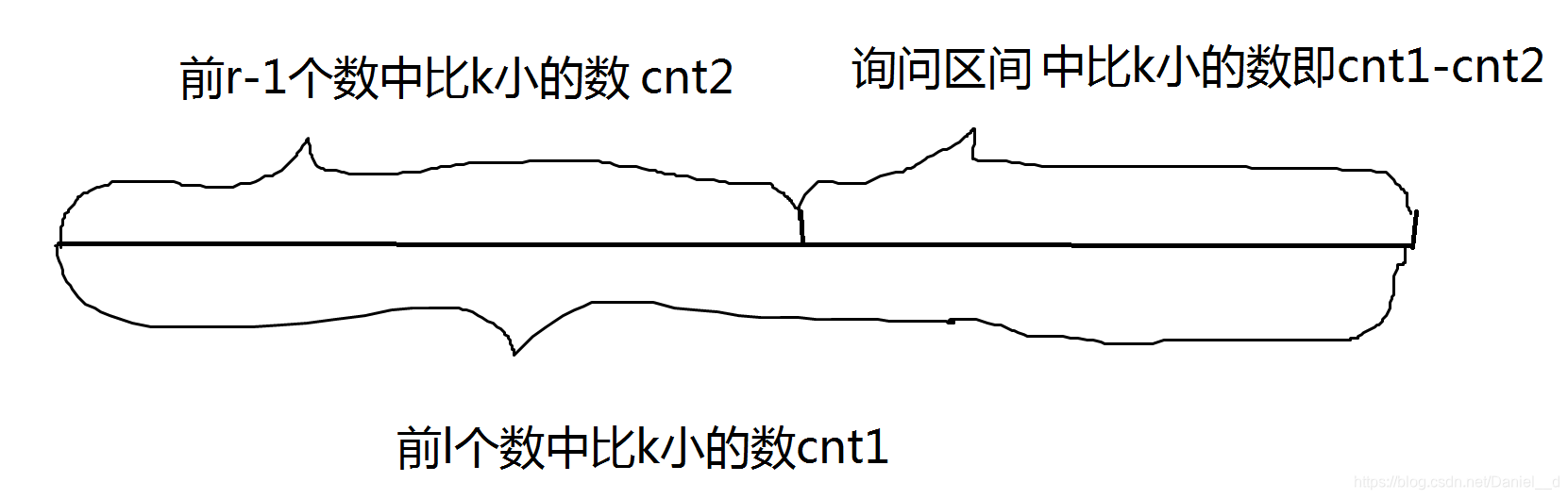
step3
4，进一步我们考虑继续优化二分，详解如下：
step4
5，那么如何优化空间复杂度呢？
step5
step5

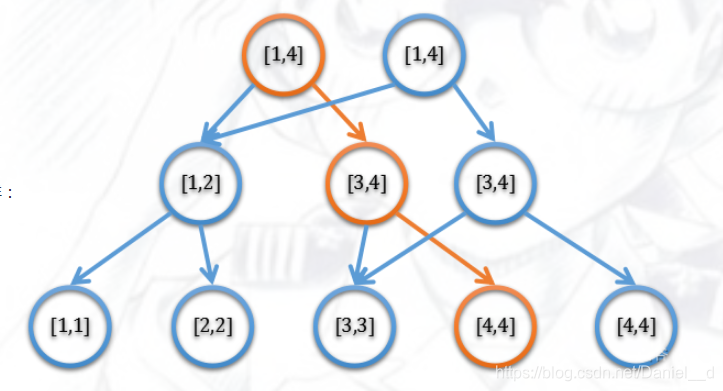
那么这样一个问题也就解决了（其时间复杂度即 $（ n + m ） l o g n$ ）
总而言之，像这样的，类似于做一个以位置（下标）区间为序的，权值线段树的前缀和的数据结构，我们称其为主席树。因此主席树的本质就是一棵棵权值线段树，或者说是一个权值线段树的前缀和。

代码1

#include<bits/stdc++.h>
#define M 200009
using namespace std;
int a[M],b[M],c[M],d[M],k,n,m,root[M];
struct node
{
	int l,r,sum;
}tree[M*32];
int build(int l,int r)
{
	k++;
	int no=k;
	int mid=(l+r)/2;
	if(l<r)//判断合法性 
	{
		tree[no].l=build(l,mid);
		tree[no].r=build(mid+1,r);
	}
	return no;//不能直接return k; 
}
int add(int p,int l,int r,int num)
{
	k++;
	int no=k;
	tree[no]=tree[p];
	tree[no].sum++;
	int mid=(l+r)>>1;
	if(l<r)
	{
		if(num<=mid) 
			tree[no].l=add(tree[p].l,l,mid,num);
		else 
			tree[no].r=add(tree[p].r,mid+1,r,num);
	}	
	return no;
}
int query(int lx,int ly,int l,int r,int num)
{
	if(l==r)
		return l;
	int temp=tree[tree[ly].l].sum-tree[tree[lx].l].sum;
	int mid=(l+r)>>1;
	if(num<=temp)//注意num<=temp,可以手动推理一下 
		return query(tree[lx].l,tree[ly].l,l,mid,num);
	else
		return query(tree[lx].r,tree[ly].r,mid+1,r,num-temp);//注意num-temp 
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		b[i]=a[i];
		c[i]=a[i];
	}
	sort(b+1,b+n+1);
	for(int i=1;i<=n;i++)//离散化处理 
	{
		a[i]=lower_bound(b+1,b+n+1,c[i])-b;
		d[a[i]]=c[i];
	}
	root[0]=build(1,n);//建立一棵空树 
	for(int i=1;i<=n;i++)
		root[i]=add(root[i-1],1,n,a[i]);
	for(int i=1;i<=m;i++)
	{
		int tx,ty,kk;
		scanf("%d%d%d",&tx,&ty,&kk);
		printf("%d\n",d[query(root[tx-1],root[ty],1,n,kk)]);
	}
	return 0;
}

代码2（yyr）

#include<bits/stdc++.h>
#define M 200009
using namespace std;
int n,m,len,cnt,a[M],b[M],rt[M];
struct tree
{
	int l,r,sum;
}tr[M*32];
int query(int x,int y,int l,int r,int k)
{
	if(l==r)
		return l;
	int mid=(l+r)>>1;
	if(tr[tr[x].l].sum-tr[tr[y].l].sum>=k)
		return query(tr[x].l,tr[y].l,l,mid,k);
	else
		return query(tr[x].r,tr[y].r,mid+1,r,k-tr[tr[x].l].sum+tr[tr[y].l].sum);
}
void build(int y,int &x,int l,int r,int val)
{
	x=++cnt;
	tr[x]=tr[y];
	++tr[x].sum;
	if(l==r)
		return;
	int mid=(l+r)>>1;
	if(val<=mid)
		build(tr[y].l,tr[x].l,l,mid,val);
	else
		build(tr[y].r,tr[x].r,mid+1,r,val);
	return;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		b[i]=a[i];
	}
	sort(b+1,b+n+1);
	len=unique(b+1,b+n+1)-b-1;
	for(int i=1;i<=n;i++)
	{
		a[i]=lower_bound(b+1,b+len+1,a[i])-b;
		build(rt[i-1],rt[i],1,len,a[i]);
	}
	for(int i=1;i<=m;i++)
	{
		int l,r,k;
		scanf("%d%d%d",&l,&r,&k);
		printf("%d\n",b[query(rt[r],rt[l-1],1,len,k)]);
	}
	return 0;
}