扫描线算法详解-优快云博客

191104-扫描线

例题引入：P5490

解析

题目要求我们求诸多的矩形的面积并，于是我们考虑求面积的方法，对于一个不规则的图形我们很难直接用公式来计算，于是我们考虑将原图形分割成诸多规则的图形，如下图：

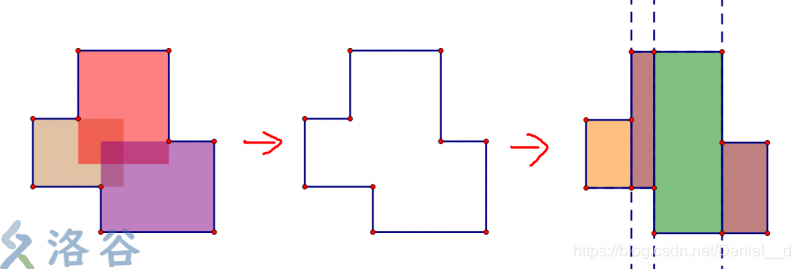
那么我们考虑如何计算每一块的面积呢，我们考虑假想一条线，从这个图形扫过，每经过一个拐点，便计算一次刚刚扫描过的规则图形的面积，然后再累加起来，如下图：
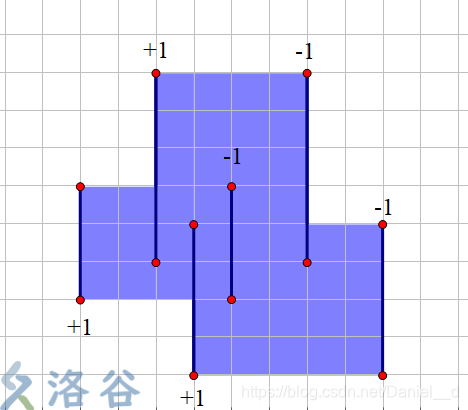
于是我们便可以将一个矩形划分成两条线，记为2个四元组 $(x 1, y 1, y 2, 1)$ 和 $(x 2, y 1, y 2, - 1)$ 然后用线段树来维护，如下图：
在这里插入图片描述

模板

#include<bits/stdc++.h>
#define int long long
#define M 200006
using namespace std;
int n,m,c[M],ans,len,val[M],x_1,x_2,y_1,y_2,maxn=(1<<31);
struct qrx{
	int yh,yl,x,z;
}e[M*2];
struct dq{
	int l,r,cnt,len;
}tr[10*M];//数组要开大点 
bool comp(qrx a,qrx b){
	if(a.x!=b.x) return a.x<b.x;
	return a.z>b.z;//如果有重边，必须将矩形的入边放在出边之前
}
void pushup(int k){
	if(tr[k].l==maxn&&tr[k].r==maxn) return;//保证不达上下最大端点
	if(tr[k].cnt) tr[k].len=val[tr[k].r+1]-val[tr[k].l];//注意是tr[k].r+1//如果该区间已经被覆盖，那么它的len即为该区间长度
	else tr[k].len=tr[k<<1].len+tr[k<<1|1].len;//反之等于其左右子节点的被覆盖的长度之和
}
void build(int k,int l,int r){
	tr[k].l=l;
	tr[k].r=r;
	if(l==r) return;
	int mid=(l+r)>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
}
void add(int k,int l,int r,int num){
	if(l<=tr[k].l&&tr[k].r<=r){
		tr[k].cnt+=num;
		pushup(k);
		return;
	}
	int mid=(tr[k].l+tr[k].r)>>1;
	if(l<=mid) add(k<<1,l,r,num);
	if(r>mid) add(k<<1|1,l,r,num);
	pushup(k);
}
signed main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
		scanf("%lld%lld%lld%lld",&x_1,&y_1,&x_2,&y_2);
		e[++m].x=x_1;
		e[m].yh=y_2;
		e[m].yl=y_1;
		e[m].z=1;
		c[m]=y_1;
		e[++m].x=x_2;
		e[m].yh=y_2;
		e[m].yl=y_1;
		e[m].z=-1;
		c[m]=y_2;
	}
	sort(c+1,c+m+1);
	len=unique(c+1,c+m+1)-c-1;
	for(int i=1;i<=m;i++){
		int pos1=lower_bound(c+1,c+len+1,e[i].yh)-c;
		int pos2=lower_bound(c+1,c+len+1,e[i].yl)-c;//对y左边离散化
		val[pos1]=e[i].yh;
		val[pos2]=e[i].yl;
		maxn=max(pos1,maxn);
		e[i].yh=pos1;
		e[i].yl=pos2;
	}
	sort(e+1,e+m+1,comp);//按x坐标的大小升序排序
	build(1,1,m);
	for(int i=1;i<=m;i++){
		add(1,e[i].yl,e[i].yh-1,e[i].z);//区间覆盖(注意是e[i].yh-1)
		ans+=(tr[1].len*(e[i+1].x-e[i].x));
	}
	printf("%lld",ans);
	return 0;
}

例题

T1 Stars in Your Window

解析

该题有一个非常巧妙的转化，首先因为矩形大小固定，因此矩形可以由它的任意一个顶点确定，我们便考虑它的右上角顶点，因此对于一颗星星 $(x, y)$ ,能圈住这颗星星的矩形右上角的坐标的范围也是一个矩形，如下图所示：

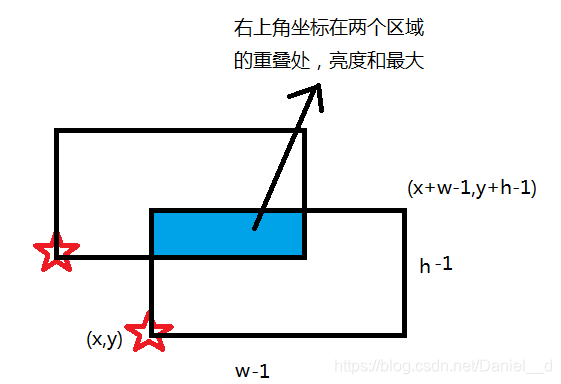
因此问题转化为了：平面上有若干个区域，每个区域内都带有一个权值，求在哪坐标上重叠的区域权值和最大，因此扫描线扫一遍，维护一个最大值即可；

但是该题还有一个坑点，就是边框所覆盖的星星不算，因此我们需要考虑如何处理边界条件，因为，所有坐标都是整数，所以，我们不妨将所有星星都向左，向下平移 $0.5$ 个单位，然后不妨再假设圈住星星的矩形顶点的坐标都为整数，于是上图的左上角为 $(x, y)$ ,右上角为 $(x + w - 1, y + h - 1)$

题解

#include  <cmath>
#include  <cstdio>
#include  <climits>
#include  <cstring>
#include  <cstdlib>
#include  <iostream>
#include  <algorithm>
#define int long long
#define M 200006 
using namespace std;
int n,ans,len,w,h,c[M];
struct qrx{
	int x,yl,yh,w;
}e[M*2];
struct dq{
	int l,r,maxn,add;
}tr[10*M];
bool comp(qrx a,qrx b){
	if(a.x!=b.x) return a.x<b.x;
	return a.w>b.w;
}
void pushdown(int k){
	if(tr[k].l==tr[k].r) return;
	tr[k<<1].add+=tr[k].add;
	tr[k<<1|1].add+=tr[k].add;
	tr[k<<1].maxn+=tr[k].add;
	tr[k<<1|1].maxn+=tr[k].add;
	tr[k].add=0;
}
void build(int k,int l,int r){
	tr[k].l=l;
	tr[k].r=r;
	if(l==r) return;
	int mid=(l+r)>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
}
void add(int k,int l,int r,int val){
	if(tr[k].l>=l&&tr[k].r<=r){
		tr[k].add+=val;
		tr[k].maxn+=val;
		return;
	}
	pushdown(k);
	int mid=(tr[k].l+tr[k].r)>>1;
	if(l<=mid) add(k<<1,l,r,val);
	if(r>mid) add(k<<1|1,l,r,val);
	tr[k].maxn=max(tr[k<<1].maxn,tr[k<<1|1].maxn);
}
void clear(){
	memset(e,0,sizeof(e));
	memset(tr,0,sizeof(tr));
	ans=0;
}
signed main(){
	int x,y,z;
	while(scanf("%lld%lld%lld",&n,&w,&h)!=EOF){
		clear();
		for(int i=1;i<=n;i++){
			scanf("%lld%lld%lld",&x,&y,&z);
			e[i]=(qrx){x,y,y+h-1,z};
			e[i+n]=(qrx){x+w-1,y,y+h-1,-z};
			c[i]=y;
			c[i+n]=y+h-1;
		}
		sort(c+1,c+n*2+1);
		len=unique(c+1,c+2*n+1)-c-1;
		for(int i=1;i<=n*2;i++){
			e[i].yl=lower_bound(c+1,c+len+1,e[i].yl)-c;
			e[i].yh=lower_bound(c+1,c+len+1,e[i].yh)-c;
		}
		build(1,1,len);
		sort(e+1,e+2*n+1,comp);
		for(int i=1;i<=2*n;i++){
			add(1,e[i].yl,e[i].yh,e[i].w);
			ans=max(ans,tr[1].maxn);
		}
		printf("%lld\n",ans);
	}
	return 0;
}

T2 窗口的星星

同上，两题基本相同

T3 覆盖的面积

解析

简化题意：其实就是求n个矩形的矩形交，因此其余操作都不变，只是在pushup的时候，要多维护一个len2值，即被覆盖了两次以上的长度，同时，在求矩形并的时候，不用下推，就是说如果1-10区域被覆盖一次，表示1-5 和6-10的节点中表示覆盖的值仍然是0，而这次，必须要把1-10覆盖的区域下推，保证1-10其左子树右子树及以下所有树节点都必须更新。

题解

#include<bits/stdc++.h>
#define M 10006
using namespace std;
double val[M],c[M*2],ans;
int t,n,len;
struct qrx{
	double x,yl,yh;
	int w;
}e[M*2];
struct dq{
	int l,r,cnt;
	double len1,len2;
}tr[M*10];
bool comp(qrx a,qrx b){
	if(a.x!=b.x) return a.x<b.x;
	return a.w>b.w;
}
void pushup(int k){
	if(tr[k].cnt){
		tr[k].len1=val[tr[k].r+1]-val[tr[k].l];
		tr[k].len2=tr[k<<1].len2+tr[k<<1|1].len2;
		if(tr[k].cnt>1) tr[k].len2=tr[k].len1;
	}
	else if(tr[k].l==tr[k].r) tr[k].len1=tr[k].len2=0;
	else{
		tr[k].len1=tr[k<<1].len1+tr[k<<1|1].len1;
		tr[k].len2=tr[k<<1].len2+tr[k<<1|1].len2;
	}
}
void build(int k,int l,int r){
	tr[k].l=l;
	tr[k].r=r;
	if(l==r) return;
	int mid=(l+r)>>1;
	build(k<<1,l,mid);
	build(k<<1|1,mid+1,r);
}
void add(int k,int l,int r,int v){
	if(tr[k].l>=l&&tr[k].r<=r){
		tr[k].cnt+=v;
		pushup(k);
		if(tr[k].l==tr[k].r) return;
	}
	int mid=(tr[k].l+tr[k].r)>>1;
	if(l<=mid) add(k<<1,l,r,v);
	if(r>mid) add(k<<1|1,l,r,v);
	pushup(k);
}
void clear(){
	memset(tr,0,sizeof(tr));
	memset(e,0,sizeof(e));
	ans=0; 
} 
int main(){
	double x_1,x_2,y_1,y_2;
	scanf("%d",&t);
	while(t--){
		clear();
		scanf("%d",&n);
		for(int i=1;i<=n;i++){
			scanf("%lf%lf%lf%lf",&x_1,&y_1,&x_2,&y_2);
			e[i].x=x_1;e[i].yl=y_1;e[i].yh=y_2;e[i].w=1;
			e[i+n].x=x_2;e[i+n].yl=y_1;e[i+n].yh=y_2;e[n+i].w=-1;
			c[i]=y_1;
			c[i+n]=y_2;
		}
		sort(c+1,c+2*n+1);
		len=unique(c+1,c+2*n+1)-c-1;
		for(int i=1;i<=n*2;i++){
			int pos1=lower_bound(c+1,c+len+1,e[i].yh)-c;
			int pos2=lower_bound(c+1,c+len+1,e[i].yl)-c;
			val[pos1]=e[i].yh;
			val[pos2]=e[i].yl;
			e[i].yh=pos1;
			e[i].yl=pos2;
		}
		build(1,1,len);
		sort(e+1,e+2*n+1,comp);
		for(int i=1;i<=2*n;i++){
			add(1,(int)e[i].yl,(int)e[i].yh-1,e[i].w);
			ans+=(tr[1].len2*(e[i+1].x-e[i].x));
		}
		printf("%.2lf\n",ans); 
	}
	return 0;
}

T4 Picture

#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
const int manx=5010;
struct Edge
{
    int x1,x2;
    int y;
    int f;
    void change()
    {
        if(x1>x2)
            swap(x1,x2);
        return ;
    }
};
struct node
{
    int f;//有多少条不想交的线段
    int ha;//是否被整体覆盖，不下传
    int len;//总共长度
    int fl,fr;//左右端点是否被覆盖，在合并时会用到
    int l,r;//实际左右端点
};
int te,tx,k;
Edge line[manx<<1];
int base[manx<<1];
int datx[manx<<1];
node t[manx<<5];
void add(int a,int b,int c,int d)
{
    if(b>d) swap(b,d);
    int x1=min(a,c),x2=max(a,c);
    line[++te].x1=x1;
    line[te].x2=x2;//x1，x2为左右端点，y为横坐标
    line[te].y=b;
    line[te].f=1;//这里是精髓，下边是一个矩阵的开始，上边是一个矩阵的结束，如此处理，我们到时候就可以直接传进更新扫描线的函数里，就不用判断了
    line[++te].x1=x1;
    line[te].x2=x2;
    line[te].y=d;
    line[te].f=-1;
}
bool compare(const Edge &a,const Edge &b)
{
    return a.y==b.y ? a.f > b.f : a.y < b.y;
}
void make_base()
{
    int now=0x7fffffff;
    for(int i=1;i<=tx;i++)
        if(now!=datx[i])
        {
            now=datx[i];
            base[++k]=now;
        }//简简单单的去重
    return ;
}
void build(int root,int l,int r)
{
    t[root].f=0;t[root].len=0;
    t[root].fl=t[root].fr=0;
    t[root].l=base[l];t[root].r=base[r+1];//因为是存的是节点之间的间隙，而且离散化了，所以说在处理左右的时候一定要小心，至于为什么r要+1，因为我是第i个点后的间隙的标号为i
    if(l==r)    return ;//剩下的就很普通了
    int mid=(l+r)>>1;
    build(root<<1,l,mid);
    build(root<<1|1,mid+1,r);
    return ;
}
int check(int val)
{
    int l=1,r=k;
    int mid;
    while(l<r)
    {
        mid=(l+r)>>1;
        if(base[mid]<val)   l=mid+1;
        else    r=mid;
    }
    return l;
}
void push_up(int root,int l,int r)
{
    if(t[root].ha)//如果这个节点被整体覆盖，ha永远也不会变成负数。为什么，可以自己小小的思考一下
    {
        t[root].len=t[root].r-t[root].l;//计算长度
        t[root].fl=t[root].fr=1;//左右端点都被覆盖
        t[root].f=1;//其中有一条线段
        return ;
    }//此处永远不会出现l==r的情况
    else//一般情况
    {
        t[root].len=t[root<<1].len+t[root<<1|1].len;//合并
        t[root].fl=t[root<<1].fl;//大区间的左端点
        t[root].fr=t[root<<1|1].fr;//大区间的右端点
        t[root].f=t[root<<1].f+t[root<<1|1].f-(t[root<<1].fr&t[root<<1|1].fl);//如果左儿子的右端点和右儿子的左端点都被覆盖，那条数就要减1
        return ;
    }
}
void updata(int root,int l,int r,int al,int ar,int k)
{
    if(l>ar||r<al)  return ;
    if(l>=al&&r<=ar)
    {
        t[root].ha+=k;//蛤呸，ha为被整体覆盖的次数，有可能被多次覆盖
        push_up(root,l,r);//更新
        return ;
    }
    int mid=(l+r)>>1;
    updata(root<<1,l,mid,al,ar,k);
    updata(root<<1|1,mid+1,r,al,ar,k);
    push_up(root,l,r);//合并，这里没有push_down
}
int main()
{
    int n;
    scanf("%d",&n);
    int a,b,c,d;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d%d",&a,&b,&c,&d);
        add(a,b,c,d);//保存边，我们这里只需要存与我们扫描线平行的边，然后我是自下而上的。所以我存的是上下边，然后请仔细看add函数   -》add
        datx[++tx]=a,datx[++tx]=c;//用于离散化的数组，当然数据小的话可以不离散化
    }
    sort(line+1,line+1+te,compare);//排序，有重边一定要下边先被处理
    sort(datx+1,datx+1+tx);//离散化
    make_base();//真离散化
    build(1,1,k-1);//建树，注意k为离散化后的坐标个数，这里要建立k-1个叶子节点，线段树中存的是相邻两个坐标之间的间隙
    int ans=0; //周长
    int last=0;//用于记录两次扫描的被覆盖的长度的变量
    for(int i=1;i<=te;i++)
    {
        int pos1=check(line[i].x1),pos2=check(line[i].x2);//二分查找离散化后的位置
        printf("%d %d\n",pos1,pos2);
		printf("%d %d\n",line[i].x1,line[i].x2);
        updata(1,1,k-1,pos1,pos2-1,line[i].f);//更新，这里就体现出我们标记上下边的好处了
        int pas=t[1].len;//最近一次扫描的长度
        ans+=abs(last-pas);//处理平行边
        ans+=t[1].f*2*(line[i+1].y-line[i].y);//处理垂直边，一定要与后一个待扫描线之间的距离
        last=pas; //迭代
        printf("%d\n",last);
    }
    printf("%d",ans);
}