Coding Practice，48天强训（8）

最新推荐文章于 2025-12-01 22:20:41 发布

原创最新推荐文章于 2025-12-01 22:20:41 发布 · 407 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构 #动态规划

Topic 1：求最小公倍数

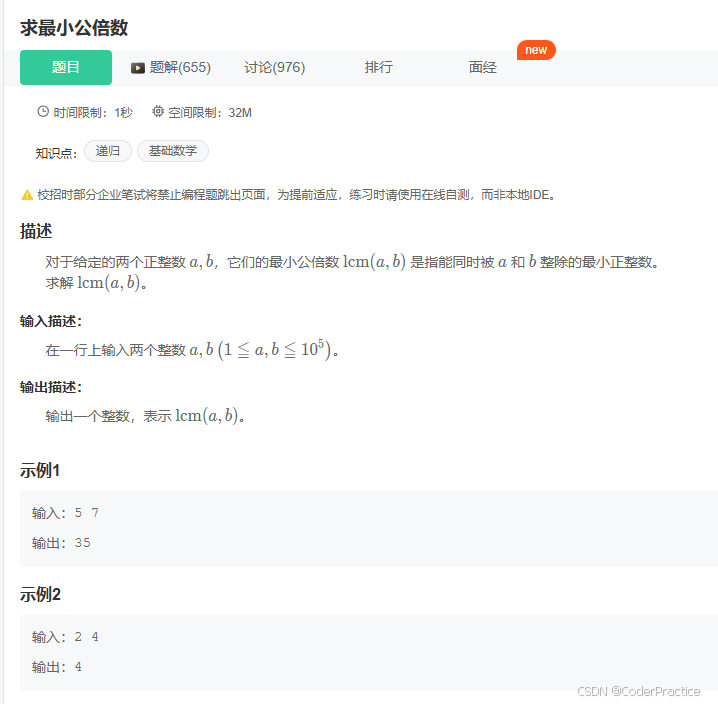
两百多天前用C做过这个题目，结果今天去看自己写的代码感觉全忘了，惭愧惭愧，重新用C++写一遍，顺便复习一下辗转相除法，数学很重要啊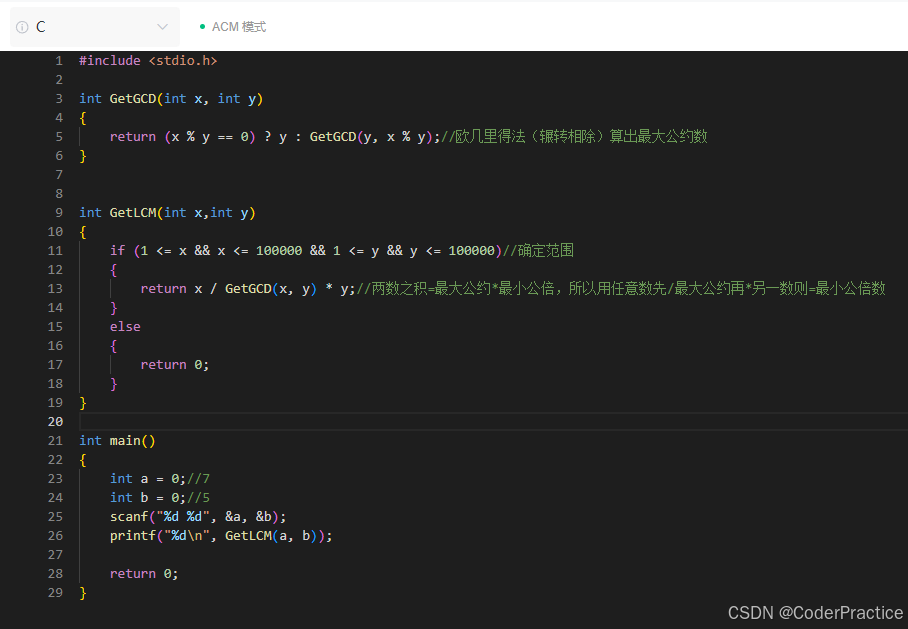

最大公约/因数(GCD-Greatest Common Divisor)——两个或多个整数共有约数中最大的一个

最小公倍数(LCM-Least Common Multiple)——两个或多个整数的最小的共同倍数

演算过程可以看欧几里得演算法(辗转相除法)_哔哩哔哩_bilibili，个人认为最简单易懂的一个演算了

#include <iostream>
using namespace std;


int gcd(int a, int b)
{
    return (a % b == 0) ? b : gcd(b, a % b);
}

int main() 
{
    int a,b;
    cin >> a >> b;
    if(a >= 1 && a <= 100000 && b >= 1 && b <= 100000) 
    {
        // 公式：两数之积 = gcd * lcm  所以   lcm = 两数之积/gcd
        cout << a*b/gcd(a,b) << endl;
    }
    return 0;
}

暂时理解不了没有关系，这种比较经典的算法，体量也小，可以先背下来，大概有个是如何运行的映像，知道是拿被除数和模之后的对象不断递归除下去就行了，之后反复复习、慢慢来理解。

Topic 2：数组中的最长连续子序列

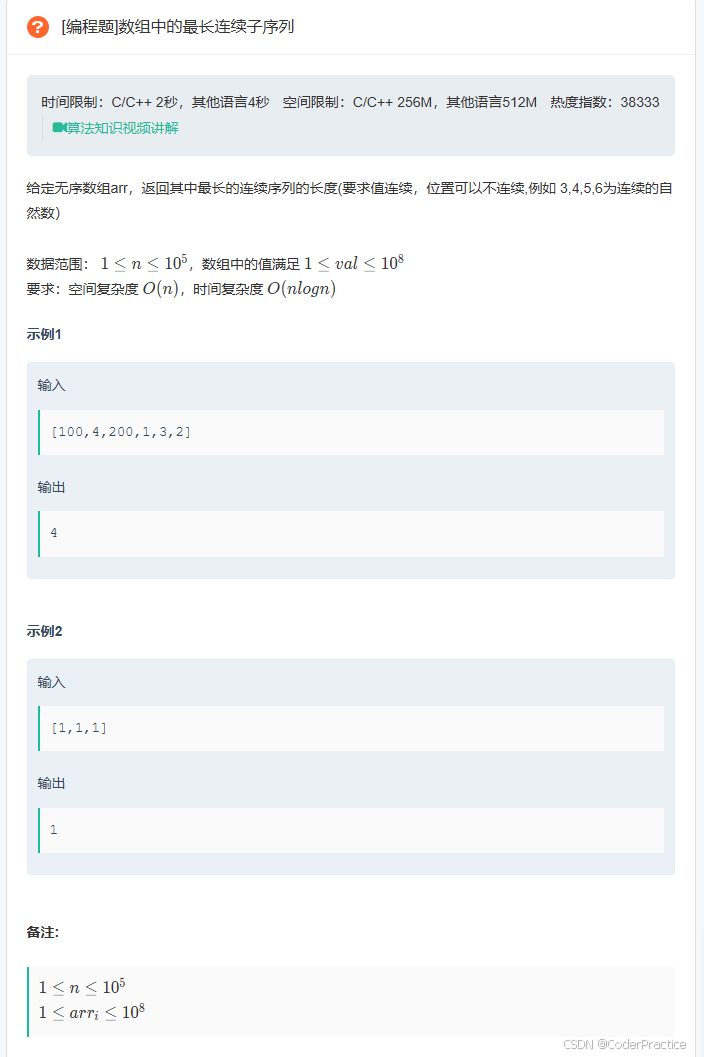
和昨天的找到字符串种最长的数字串很像，筛选条件变了一下而已,然后审题要注意，是在无序数组里任意捞元素组合，看错了题目在那儿卡了半天没通过

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * max increasing subsequence
     * @param arr int整型vector the array
     * @return int整型
     */
    int MLS(vector<int>& arr) 
    {
        if(arr.empty()) return 0;
        
        sort(arr.begin(), arr.end());
        int maxlen = 1;  // 至少有一个元素
        int curlen = 1;
        
        for(int i = 1; i < arr.size(); ++i) 
        {
            // 跳过重复元素
            if(arr[i] == arr[i-1]) continue;
            
            // 满足连续递增
            if(arr[i] == arr[i-1] + 1) 
            {
                curlen++;
                maxlen = max(maxlen, curlen);
            } 
            else 
            {
                curlen = 1;  // 重置当前长度
            }
        }
        return maxlen;
    }
};

Topic 3：字母收集

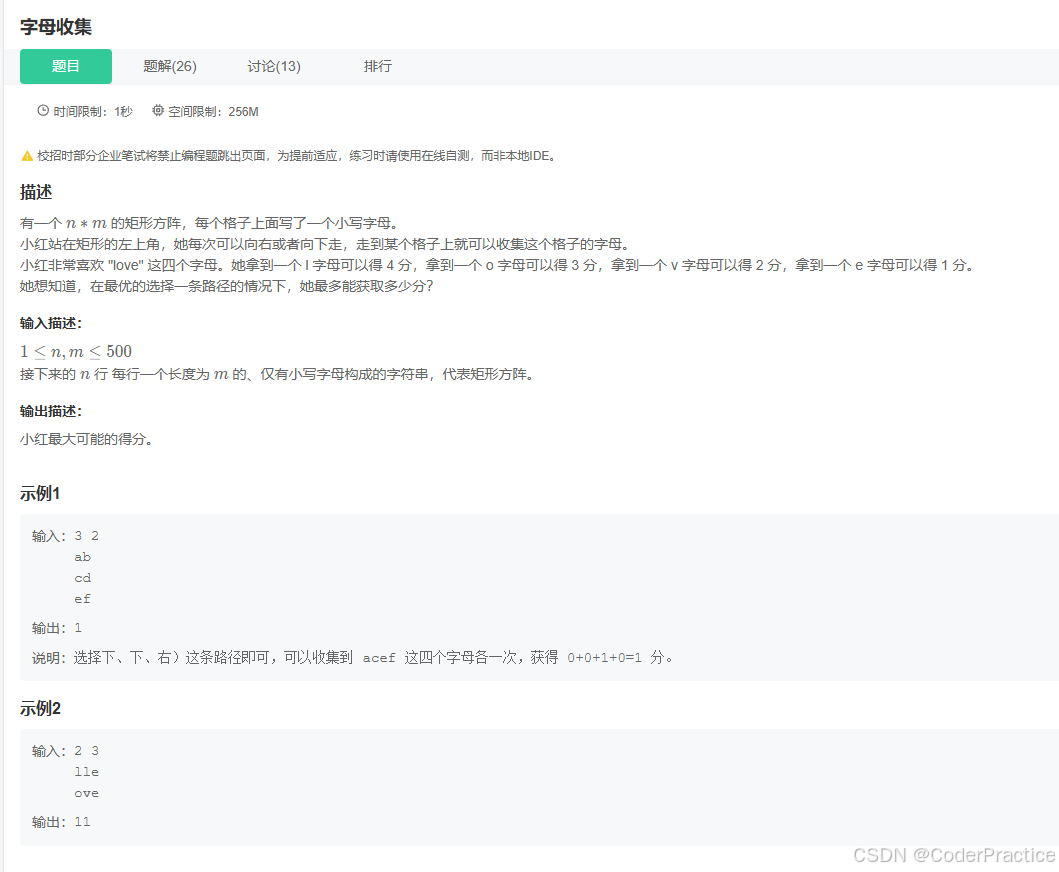
经典的动态规划问题，路径类DP问题，最大化收集路面上散落的星星，这种路径问题一般都是根据矩阵中某一个终点来计算路径，返回的是个路径信息，本题主要是求最大分数，那就更简单了，已知我们从左上角出发，每次只能下or右，也就意味着没有回头路，那么无论怎么走，最终的终点肯定是右下，它的分数也必然是最高的。那么假设图中所有的黄点都是字母e，可以的得1分，这样方便举例，那么我们可以模拟遍历分数累加的过程

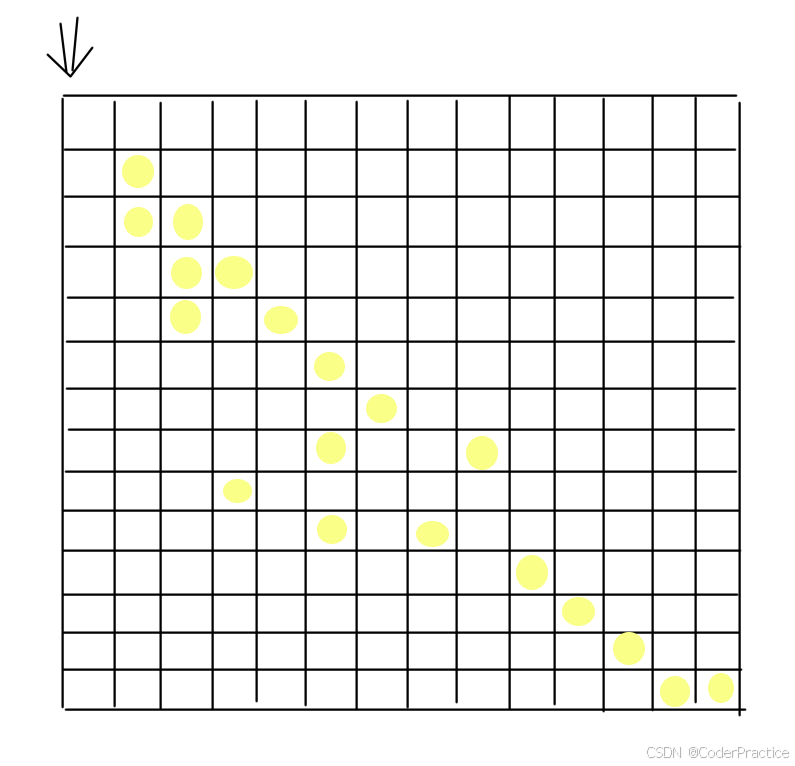
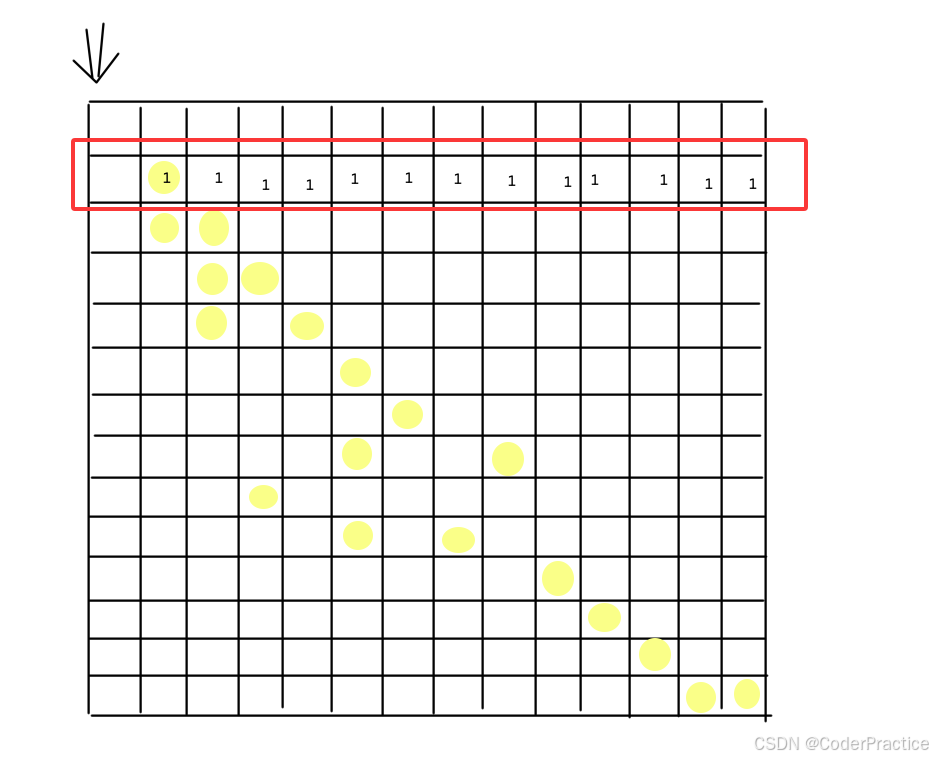
第一排遍历完填进去的最大分数就是这么个情况，因为当前格子所能获得的最大分数来源无非就是上一格的分数or左一格的分数和本格分数相加，第一排只有起点有个一分，所以如果从左到右一横条走完，也就最多1分，继续往下画一画

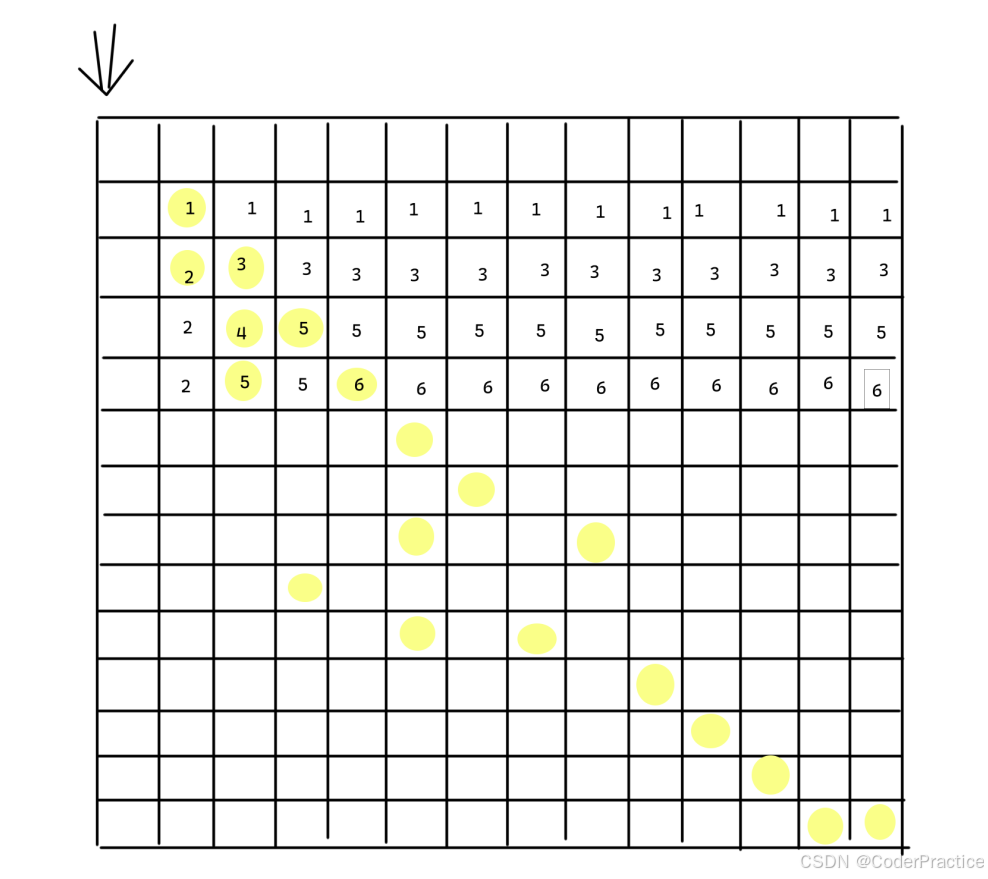
多填两行，大概遍历就是这么个事儿，根据 max(左 or 上) + 自个儿的分 = 当前格最大分，这样一路往下填，把格子填满，最后右下那个最大的分数就是答案了。

#include <iostream>
using namespace std;

int main()
{
    const int N = 510;//1≤n,m≤500
    char grid[N][N];
    int dp[N][N];
    int m, n;
    cin >> m >> n;

    for(int i = 1; i <= m; ++i)
    {
        for(int j = 1; j <= n; ++j)
        {
            cin >> grid[i][j];
        }
    }

    for(int i = 1; i <= m; i++)
    {
        for(int j = 1; j <= n; j++)
        {
            int t = 0;
            if(grid[i][j] == 'l') t = 4;
            else if(grid[i][j] == 'o') t = 3;
            else if(grid[i][j] == 'v') t = 2;
            else if(grid[i][j] == 'e') t = 1;
            dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + t;
        }
    }
    
    cout << dp[m][n] << endl;
    return 0;
}

代码记得要复习。