Coding Practice，48天强训（7）

原创已于 2025-03-26 16:15:41 修改 · 388 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #开发语言

于 2025-03-26 12:19:16 首次发布

这几天没注意看邮箱，强训前天就恢复了，虽然没这两天题目没参加，还是翻出来好好做一做，保持博客不断更

Topic 1：字符串中找出连续最长的数字串

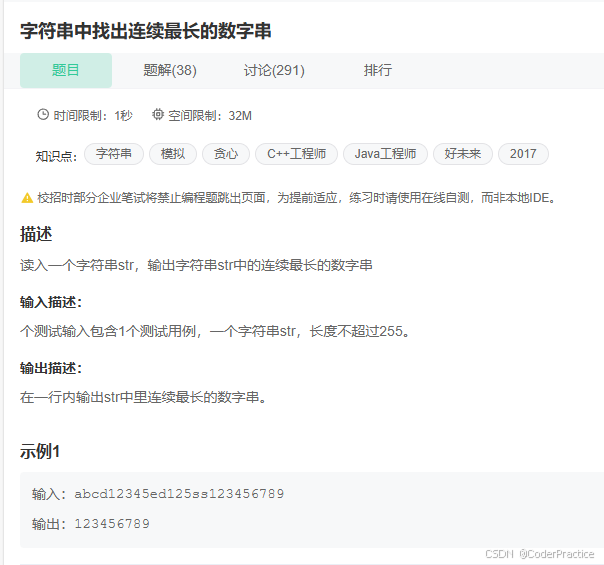
关键在于如何对数字字符串进行区分，可以考虑采用isdigit()，如果忘了就用ASCII码来区分，然后要对每个分段字符串的头部做标记，方便最后返回；

#include <iostream>
using namespace std;

int main() 
{
    string str;
    cin >> str;
    int curpos = 0, curlen = 0, maxpos = 0, maxlen = 0;
    //当前遍历的位置头下标，当前长度，最大字符串起始头下标，最大长度
    for(int i = 0; i < str.size(); ++i)
    {
        if(str[i] >= '0' && str[i] <= '9')//如果忘了isdigit(str[i])函数就用笨办法判断是否是数字
        {
            if(curlen == 0)// 不断找数字串，如果curlen为0，代表是第一次找到数字串或者是前一个数字串已经统计完毕了
            {
                curpos = i; // 从这里开始计现在遍历的数字串的头下标
            }
            ++curlen;// 更新现在所遍历数字串的长度
        }
        else// 如果没有数字了，代表遇到字符了，这一串数字串的计数就截止了
        {
            if(curlen > maxlen)// 如果当前计数的长度大于之前所计的最大长度
            {
                maxlen = curlen;// 更新最大长度
                maxpos = curpos;// 更新最大数字串的头下标
            }
            curlen = 0;// 让统计长度归零，到下一个数字串出现重新计数
        }
    }

    if(curlen > maxlen)// 如果最后是以数字结尾，跳出for循环，curlen中仍有计数，需要最后判断一次
    {
        maxlen = curlen;// 更新最大长度
        maxpos = curpos;// 更新最大数字串的头下标
    }

    // 如果忘了substr()就用笨办法，循环打印也是可以的，要灵活
    //cout << str.substr(maxpos, maxlen) << endl;
    // substr()用于从字符串中提取子字符串。根据给定的起始位置和长度，返回原字符串中从该位置开始指定长度的子字符串
    for(int i = maxpos; i < maxpos + maxlen; ++i)
    {
        cout << str[i];
    }

    return 0;
}

整体还是很简单的，四个参数控制就能实现了，复习一下isdigit() 和substr() 函数，同时要注意审题，第一遍看的时候看成了选出最长的字符串，还在那儿想半天考虑要把字符和数字串分开去计数。

Topic 2：岛屿数量 BFS/DFS

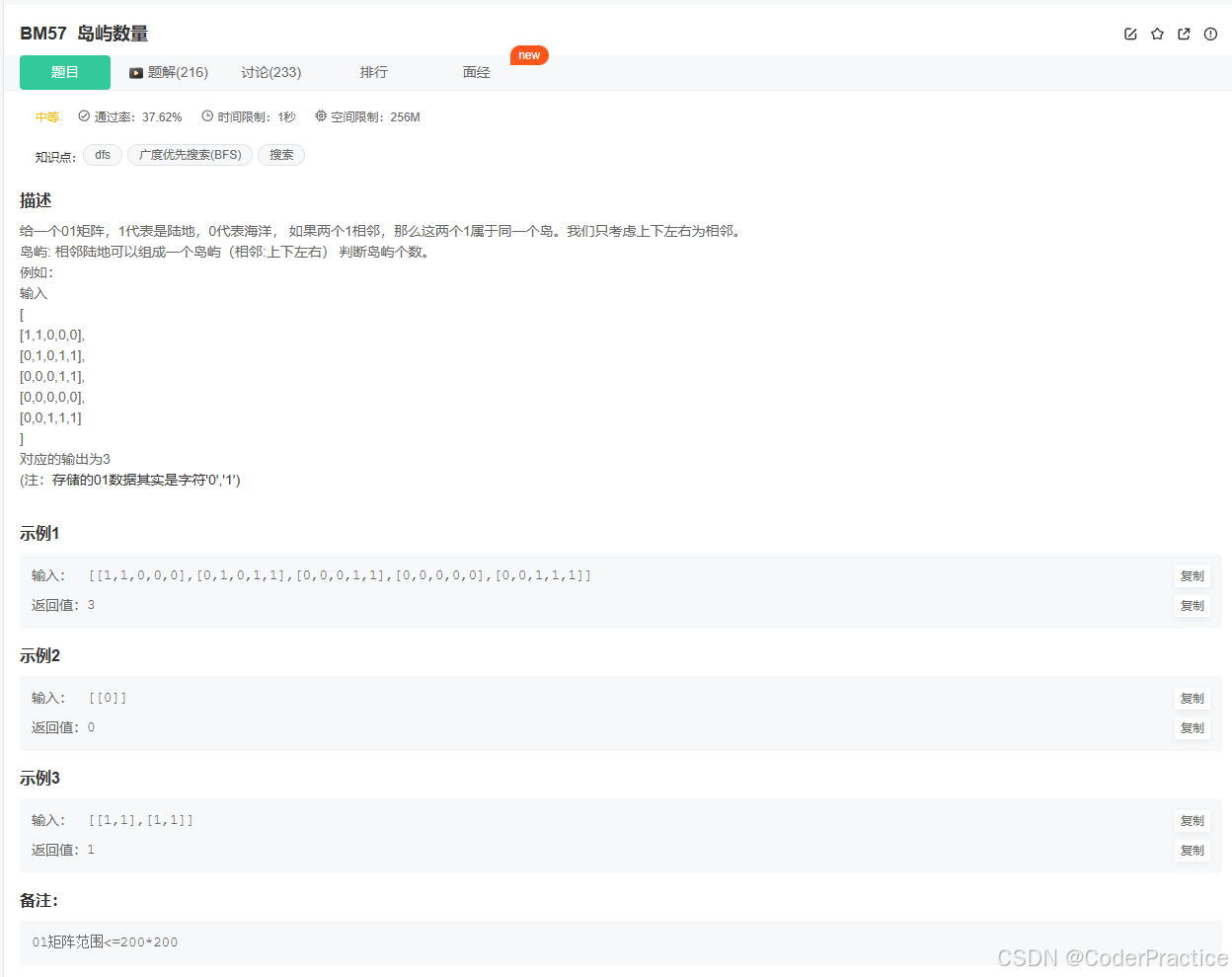
无比经典的一个搜索题目，属于是不会不是算法人级别，用BFS来解，主要注意几个要点

遍历矩阵元素进队列、操控方向的映射容器、负责表示是否遍历的bool容器

#include <queue>
#include <type_traits>
class Solution 
{
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 判断岛屿数量
     * @param grid char字符型vector<vector<>> 
     * @return int整型
     */

     vector<pair<int, int>> dir = {{0,1},{0,-1},{-1,0},{1,0}};// 用于四方向搜索，上下左右

    int solve(vector<vector<char>>& grid) 
    {
        if (grid.empty() || grid[0].empty()) return 0;// 健壮性
        int res = 0;// 岛屿数量
        int row = grid.size();
        int col = grid[0].size();
        vector<vector<bool>> vis(row, vector<bool>(col, false)); // 用来表示是否搜索过了

        for(int i = 0; i < row; ++i)
        {
            for(int j = 0; j < col; ++j)
            {
                if(grid[i][j] == '1' && vis[i][j] == false)// 发现岛屿并且没有探索过
                {
                    ++res;// ++岛屿数量
                    queue<pair<int, int>> que;// BFS遍历用的队列
                    que.push({i,j});// 另一种写法que.push(make_pair(3, 4));
                    vis[i][j] = true;// 将此区域标记为探索过

                    while (!que.empty())// BFS的核心就在于通过队列中的数据判断此次区域的搜索是否完全覆盖最广范围，若队列已无元素，代表已穷尽最广搜索范围 
                    {
                        auto cur = que.front();// 记录队头数据
                        que.pop();// 用完了可以出队了
                        int x = cur.first;// 取出x y
                        int y = cur.second;
                        for(const auto& d : dir)// 四向搜索，把最大广度范围内的所有‘1’都归到自身这个岛屿里
                        {
                            int nx = x + d.first;
                            int ny = y + d.second;
                            // 横纵轴不能越界，要是‘1’才算作岛屿一部分，还不能之前被搜索过
                            if(nx >= 0 && nx < row && ny >= 0 && ny < col && grid[nx][ny] == '1' && vis[nx][ny] == false )
                            {
                                que.push({nx, ny});// 所有都满足条件则算作一部分，入队，有后续依据此继续四向搜索的资格
                                vis[nx][ny] = true;// 标记当前‘1’为已搜索
                            }
                        }
                    }
                }
            }
        }
        return res;
    }
};

最近比较忙，就只写一个BFS的解法，之后有时间把DFS方法补上。

Topic 3：拼三角

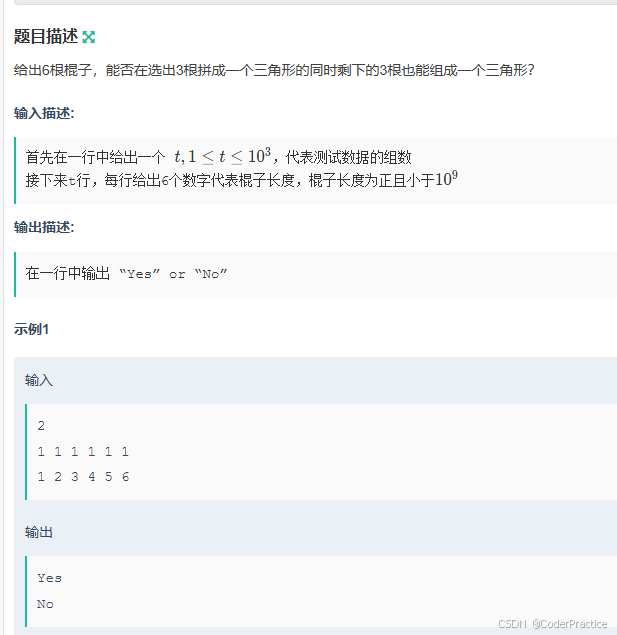
初看感觉是个小贪心，首先确定极值条件，三角形的构成条件是三角不等式——任意两边之和>第三边，所以首先6根中取3根，要找到其中差值最小的那个组合，数据量比较小，可以考虑直接暴力

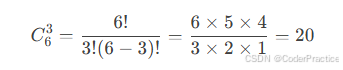
根据组合公式求出6选3有20种组合，再排除一些重复的，比如选择abc--def和def--abc实际上是一组，所以再/2,总共有10种组合，这是枚举的方式，三层for循环即可

// 检查三个数是否能组成三角形
bool isTriangle(int a, int b, int c) {
    if (a + b > c && a + c > b && b + c > a) {
        return true;
    }
    return false;
}

// 检查六根棍子是否能分成两组三角形
bool canSplitIntoTwoTriangles(vector<int>& sticks) {
    // 枚举所有 C(6,3) = 20 种组合
    for (int i = 0; i < 6; ++i) {
        for (int j = i + 1; j < 6; ++j) {
            for (int k = j + 1; k < 6; ++k) {
                // 选中的三根
                int a = sticks[i], b = sticks[j], c = sticks[k];
                // 剩下的三根
                vector<int> remaining;
                for (int m = 0; m < 6; ++m) {
                    if (m != i && m != j && m != k) {
                        remaining.push_back(sticks[m]);
                    }
                }
                int x = remaining[0], y = remaining[1], z = remaining[2];
                // 检查两组是否能组成三角形
                if (isTriangle(a, b, c) && isTriangle(x, y, z)) {
                    return true;
                }
            }
        }
    }
    return false;
}

其次还能使用DFS，这里先不写了，最后还有更好的一种更好的方法，是数学方面的优化

将长度由小到大排序，原本如果是无序序列，需要判断(a + b > c && a + c > b && b + c > a)，因为不知道abc谁大，所以都要算；现在排序后，假设由小到大是a、b、c；只用判断a + b > c即可，因为c排序后本来比a、b都大，所以从c+a or c+b都大于另一边；

然后枚举所有情况可以分析出，当012-345不能组成三角形时，后续列下的情况都无法组成，比如0号边+1号边<2号边，那么0号边+1号边在升序情况下绝对也小于3号边，因此，最终所需判断的只有四种情况——012-345 023-145 034-125 045-123

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 检查三根已排序木棍是否能构成三角形
bool isTriangle(int a, int b, int c) {
    return a + b > c;  // 只需检查最小两边和是否大于最大边
}

int main() {
    int t;
    cin >> t;
    
    while (t--) 
    {
        vector<int> sticks(6);  // 存储6根木棍长度
        // 输入木棍长度（使用常规for循环）
        for (int i = 0; i < 6; i++) 
        {
            cin >> sticks[i];
        }
        sort(sticks.begin(), sticks.end());  // 升序排序

        // 检查四种分组方式
        bool possible = false;
        
        // 情况1：前3根 vs 后3根 [0,1,2]和[3,4,5]
        if (isTriangle(sticks[0], sticks[1], sticks[2]) && 
            isTriangle(sticks[3], sticks[4], sticks[5])) 
        {
            possible = true;
        }
        
        // 情况2：[0,2,3]和[1,4,5]
        else if (isTriangle(sticks[0], sticks[2], sticks[3]) && 
                isTriangle(sticks[1], sticks[4], sticks[5])) 
        {
            possible = true;
        }
        
        // 情况3：[0,3,4]和[1,2,5]
        else if (isTriangle(sticks[0], sticks[3], sticks[4]) && 
                isTriangle(sticks[1], sticks[2], sticks[5])) 
        {
            possible = true;
        }
        
        // 情况4：[0,4,5]和[1,2,3]
        else if (isTriangle(sticks[0], sticks[4], sticks[5]) && 
                isTriangle(sticks[1], sticks[2], sticks[3])) 
        {
            possible = true;
        }
        
        cout << (possible ? "Yes" : "No") << endl;
    }
    return 0;
}

后续自己还要复习，学了Lambda表达式之后要再回来写一遍，更简洁更优雅，先把AI写的贴上

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    int t; cin >> t;  // 输入测试用例数量
    while (t--) {
        vector<int> s(6);  // 存储6根木棍长度
        for (int& x : s) cin >> x;  // 输入木棍长度
        sort(s.begin(), s.end());  // 排序后更容易验证三角形条件

        // 四种分组方式（索引组合）：
        // 1. 前3根 vs 后3根 [0,1,2]~[3,4,5]
        // 2. [0,2,3]~[1,4,5]
        // 3. [0,3,4]~[1,2,5]
        // 4. [0,4,5]~[1,2,3]
        auto check = [&](int a, int b, int c) {
            return s[a]+s[b] > s[c];  // 只需检查最小两边和>最大边（因已排序）
        };

        // 检查任意分组是否同时满足两个三角形
        bool ok = 
            (check(0,1,2) && check(3,4,5)) ||  // 分组1
            (check(0,2,3) && check(1,4,5)) ||  // 分组2
            (check(0,3,4) && check(1,2,5)) ||  // 分组3
            (check(0,4,5) && check(1,2,3));    // 分组4

        cout << (ok ? "Yes" : "No") << endl;
    }
}