洛谷P1003 [NOIP2011 提高组]铺地毯题解

暴力模拟，时间复杂度只有 O(n)

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有n张地毯，编号从1到n。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

整体思路

先将地毯的位置都存储下来。地毯是从低到高叠放的，要知道最上面的地毯编号，逆序依次枚举就行了。

蒟个栗子

样例输入：
3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

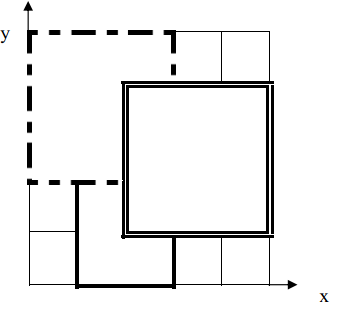
拿样例来说，共3张地毯，坐标分别是：

[ ( 1 , 0 ) , ( 3 , 3 ) ] , [ ( 0 , 2 ) , ( 3 , 5 ) ] 和 [ ( 2 , 1 ) , ( 5 , 4 ) ]。

逆序枚举，先检查第3张地毯，点 ( 2 , 2 ) 在 [ ( 2 , 1 ) , ( 5 , 4 ) ] 上，所以直接输出3。

代码实现看这里

#include<iostream>
using namespace std;
int a[10005]<