题目描述:
有一根长度为 n 个单位的木棍,棍上从 0 到 n 标记了若干位置。例如,长度为 6 的棍子可以标记如下:
给你一个整数数组 cuts ,其中 cuts[i] 表示你需要将棍子切开的位置。
你可以按顺序完成切割,也可以根据需要更改切割的顺序。
每次切割的成本都是当前要切割的棍子的长度,切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍(这两根木棍的长度和就是切割前木棍的长度)。请参阅第一个示例以获得更直观的解释。
返回切棍子的 最小总成本 。
示例 1:
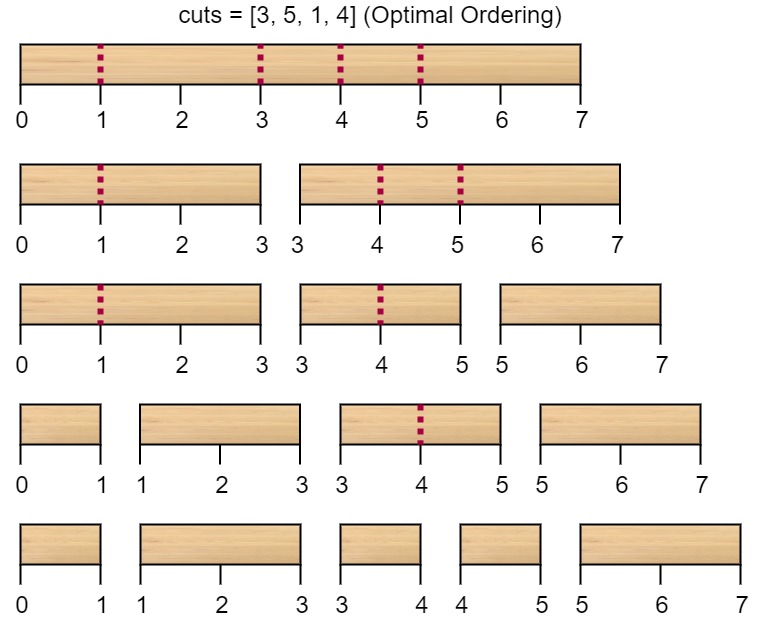
输入:n = 7, cuts = [1,3,4,5] 输出:16 解释:按 [1, 3, 4, 5] 的顺序切割的情况如下所示:
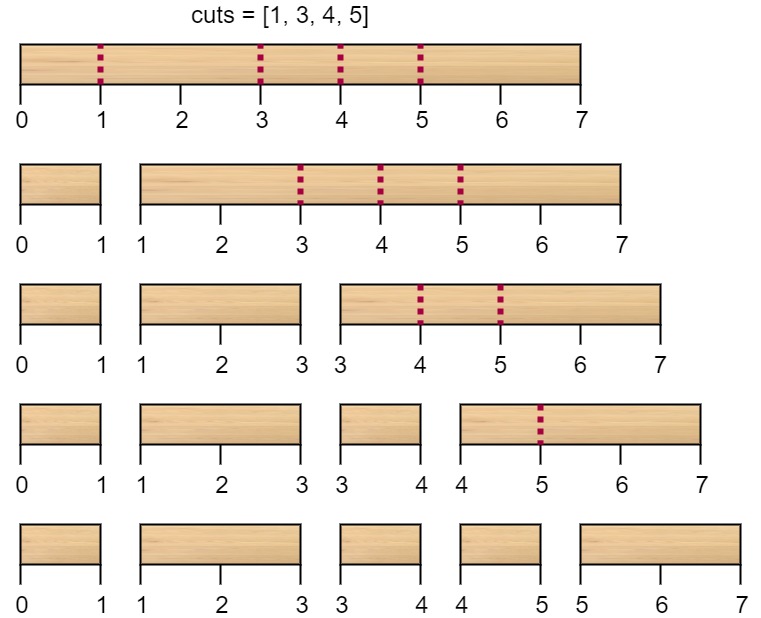
第一次切割长度为 7 的棍子,成本为 7 。第二次切割长度为 6 的棍子(即第一次切割得到的第二根棍子),第三次切割为长度 4 的棍子,最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。 而将切割顺序重新排列为 [3, 5, 1, 4] 后,总成本 = 16(如示例图中 7 + 4 + 3 + 2 = 16)。
示例 2:
输入:n = 9, cuts = [5,6,1,4,2] 输出:22 解释:如果按给定的顺序切割,则总成本为 25 。总成本 <= 25 的切割顺序很多,例如,[4, 6, 5, 2, 1] 的总成本 = 22,是所有可能方案中成本最小的。
提示:
2 <= n <= 10^61 <= cuts.length <= min(n - 1, 100)1 <= cuts[i] <= n - 1cuts数组中的所有整数都 互不相同
解题思路
1、首先,我们需要对给定的切割点数组进行排序,并在其两端添加0和n作为新的切割点。
2、使用一个二维动态规划数组dp来存储子问题的解。dp[i][j]表示在当前待切割的木棍的左端点为cuts[i],右端点为cuts[j]时,将木棍全部切开的最小总成本。
3、初始化dp数组,对于相邻的两个点,切割成本为0。
4、使用三层循环来填充dp数组。外层循环遍历所有可能的区间长度,从大到小;中层循环遍历所有可能的左端点;内层循环遍历所有可能的分割点,并更新dp[i][j]的值。
5、最终返回dp[0][m+1],即整个木棍从0到n被完全切割的最小成本。
class Solution {
public:
int minCost(int n, vector<int>& cuts) {
int m = cuts.size();
sort(cuts.begin(), cuts.end());
vector<int> cutss(m + 2);
cutss[0] = 0;
cutss[m + 1] = n;
for (int i = 0; i < m; ++i) {
cutss[i + 1] = cuts[i];
}
vector<vector<int>> dp(m + 2, vector<int>(m + 2, 0));
for (int len = 2; len <= m + 1; ++len) {
for (int i = 0; i <= m + 1 - len; ++i) {
int j = i + len;
dp[i][j] = INT_MAX;
for (int k = i + 1; k < j; ++k) {
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
}
dp[i][j] += cutss[j] - cutss[i];
}
}
return dp[0][m + 1];
}
};




















 1559
1559

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








