洛谷 P1002 过河卒（递推）

最新推荐文章于 2025-10-22 21:10:15 发布

原创最新推荐文章于 2025-10-22 21:10:15 发布 · 922 阅读

2 ·

CC 4.0 BY-SA版权

ACM-ICPC 专栏收录该内容

238 篇文章

订阅专栏

该博客详细介绍了洛谷P1002问题——过河卒的解题思路。通过设立f[m][n]表示卒从(0,0)走到(m,n)的路径数，分析了卒的行走规则，提出递推公式，并针对特殊情况进行了说明。博主给出了避免边界错误的处理方法，并提供了AC代码。" 112952219,10536284,Hyper-V 2012 R2增强会话模式：实现高效虚拟机管理,"['虚拟化技术', 'Hyper-V管理', 'Windows Server 2012 R2', '第二代虚拟机', '增强会话']

一、题目描述

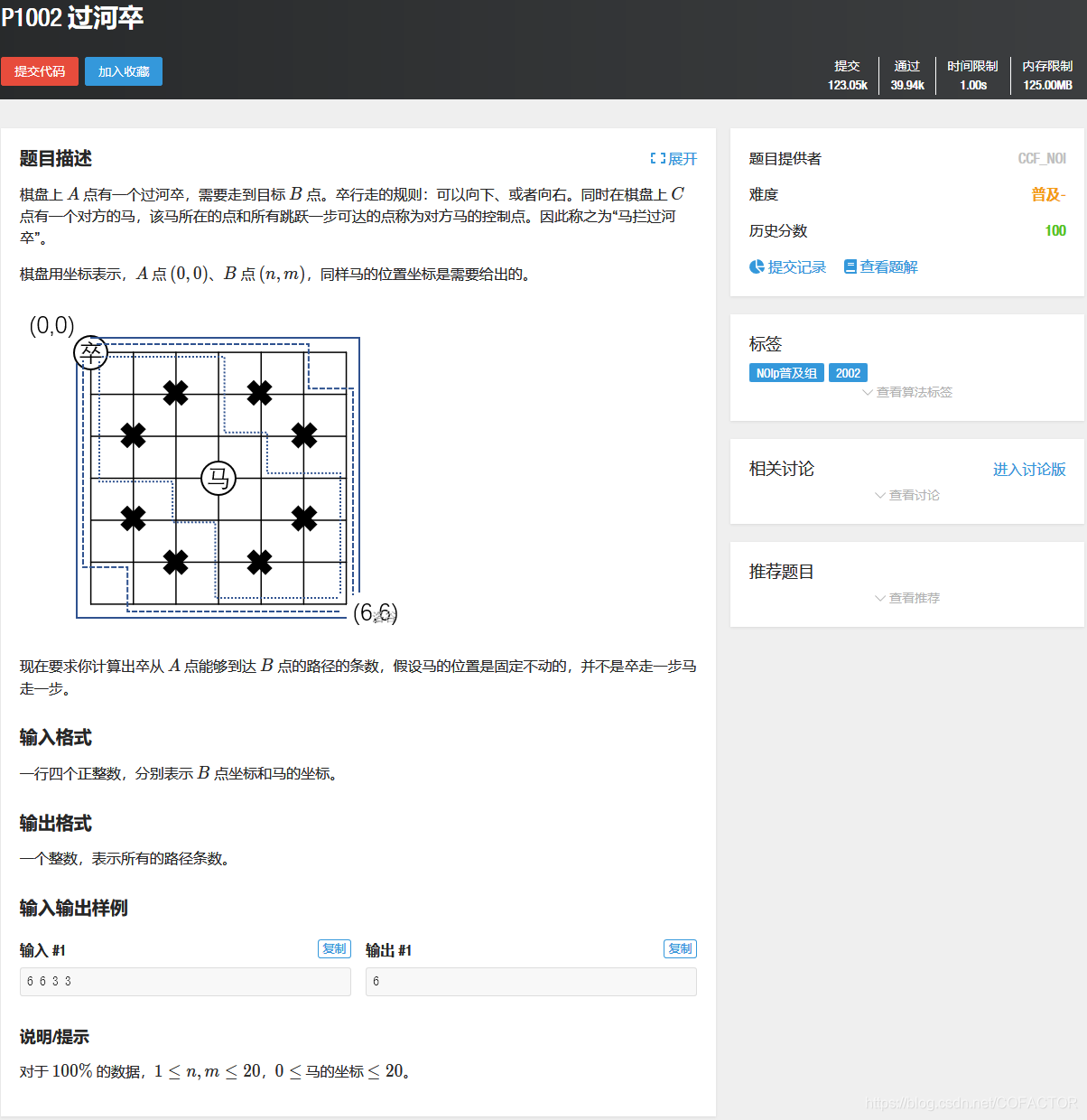
在这里插入图片描述

二、算法分析说明与代码编写指导

设 f[m][n] 为卒从 (0，0）走到（m，n）的路径数。卒只能向右走或向下走，易得递推公式的第二种情形：
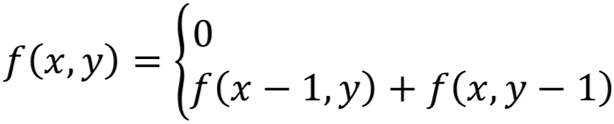
在这里插入图片描述
当某位置的正左方和正上方都为马可以跳到的点或是马本身，那么这点不可能被被卒走到，路径数为 0。我们将马所在位置和马可以跳到的八个点都标记为 -1。
这题有一个非常坑的地方：如果马可以跳至的点或者马本身在左边或上边，那么最上方一行的最右侧（最左方一列的最下侧）被标记为 -1 的点的右方（下方）也是卒不可以走到的，这些位置累计的路径数为 0。最上面一行和最左边一列的其余位置的路径数量都是 1，因为卒只能不断向右（下）走到达。如果把这些要标记 0 的地方标记为 1，只能对 1 组数据。
为了防止越界，将（m，n）和马的坐标（x，y）在处理前都加上 2。

三、AC 代码

#include<cstdio>
#pragma warning(disable:4996)
long long f[23][23], m, n, x, y;
inline long long a(const long long& x, const long long& y) {
	static long long s, t;
	if (f[x - 1][y] == -1)s = 0;
	else s = f[x - 1][y];
	if (f[x][y - 1] == -1)t = 0;
	else t = f[x][y - 1];
	return s + t;
}
inline void test() {
	puts("****TEST:****");
	for (long long i = 2; i <= m; ++i) {
		for (long long j = 2; j <= n; ++j) { printf("%11lld ", f[i][j]); }
		putchar('\n');
	}
	puts("****END TEST****");
}
int main() {
	scanf("%lld%lld%lld%lld", &m, &n, &x, &y); m += 2; n += 2; x += 2; y += 2;
	for (long long i = 2; i <= m; ++i)f[i][2] = 1;
	for (long long i = 2; i <= n; ++i)f[2][i] = 1;
	f[x - 2][y - 1] = f[x - 1][y - 2] = f[x - 2][y + 1] = f[x - 1][y + 2] = f[x + 1][y - 2] = f[x + 2][y - 1] = f[x + 1][y + 2] = f[x + 2][y + 1] = f[x][y] = -1;
	for (long long i = m; i >= 2; --i) {
		if (f[i][2] == -1) {
			for (++i; i <= m; ++i) { f[i][2] = 0; }
			break;
		}
	}
	for (long long i = n; i >= 2; --i) {
		if (f[2][i] == -1) {
			for (++i; i <= n; ++i) { f[2][i] = 0; }
			break;
		}
	}
	//test();
	for (long long i = 3; i <= m; ++i)
		for (long long j = 3; j <= n; ++j) {
			if (f[i][j] == -1)continue;
			f[i][j] = a(i, j);
			//test();
		}
	//test();
	printf("%lld\n", f[m][n]);
	return 0;
}