【梳理】数字设计基础与应用第1章数字逻辑基础 1.5 逻辑函数的化简

最新推荐文章于 2025-01-25 15:30:57 发布

原创

最新推荐文章于 2025-01-25 15:30:57 发布 · 1k 阅读

4 ·

CC 4.0 BY-SA版权

本文介绍了数字逻辑基础中的逻辑函数化简，包括代数化简法和卡诺图化简。代数化简利用逻辑定律简化逻辑表达式，卡诺图通过合并相邻项减少变量。化简目标是实现逻辑门数量和输入端最少，以达到电路最简。同时，文章提及非完全描述函数的化简策略，以及在实际应用中处理无效输入的重要性。

教材：数字设计基础与应用第二版邓元庆关宇贾鹏石会编著清华大学出版社源文档高清截图在后

1.5 逻辑函数的化简

1、显然，函数的表达式不同，对应的逻辑电路也不同。完成同样的逻辑功能，我们总是希望电路越简单越好。因为简单的电路成本低、功耗低、故障率低、研发周期短。逻辑门实现的数字电路的最简标准是：逻辑门数量最少，每个逻辑门的输入端最少。

2、由最简逻辑电路的概念可以导出最简表达式的概念。对常用的与或式、或与式而言，逻辑门最少意味着与或式的积项个数最少，或与式的和项个数最少。输入端数量最少意味着每个积项或和项中的变量个数最少。

3、代数化简法利用逻辑代数的基本定律，通过项的合并与吸收、消去冗余变量等手段来减少项的个数和变量个数。常用的基本定律有：
（1）互补律：A + A’ = 1、A·A’ = 0
（2）0-1律：A + 0 = A、A + 1 = 1、A·A’ = 0、A·1 = A
（3）对合律：A’’ = A
（4）重叠律：A + A = A、A·A = A
（5）吸收律：A + AB = A、A(A + B) = A、A+A’B = A + B、A(A’ + B) = AB、
AB + AB’ = A、(A +B)(A + B’) = A、AB + A’C + BC = AB + A’C、(A + B)(A’ + C)(B + C) = (A + B)(A’ + C)
（6）反演律：(A + B)’ = A’B’、(AB)’ = A’ + B’
前4条定律想必大家非常熟悉，需要重点记忆的就是5和6。

4、卡诺图（Karnaugh map）也是一种常用的化简方法。卡诺图的示例如下：

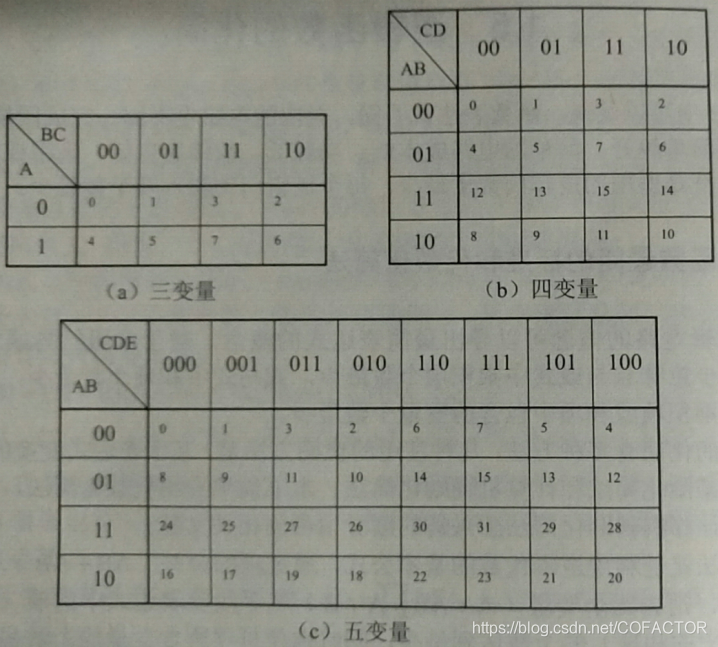
可以看出，在画卡诺图的时候，尽量将已有变量均分成两份，然后将全部可能的取值按循环码的形式分别填入第一行和第一列（除了最左上角的一格）中。第一行和第一列的变量可以调换。剩下的方格对应