主定理

主定理

备考初赛的最后三天，幸好发现了一个不会的牛逼的东西，不然在考场上可懵逼了
主定理，研究递推的时间复杂度，我说之前的递推的题都不会算呢
首先，它的形式是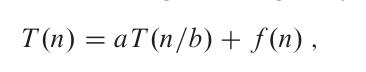
这样子的
所以我们最后的复杂度是和a和b还有f(n)这三个参数是有关系的
首先，我们计算f(n)的复杂度，也就是最后的相加的复杂度
然后，我们在计算n的复杂度也就是n=n^log b a^b下a上
然后我们需要比较一下哪一个更牛逼
怎么比较哪一个更牛逼？
比如O(1)和O(n)，O(n)和O(n²)这两个都是后者更强
比较之后，当然分了三种情况：
1.n的复杂度强
2.f的复杂度强
3.两个一样
所以根据三种情况就有三个解决方案
1.n的复杂度强，那么结果的时间复杂度为T(n)=O(n^log b a^) ，不用管为什么，直接带入
2.f的复杂度强，那么结果就是T(n)=O(f(n))，直接把f的复杂度拿过来，外面长上O /xyx
3.两个一样强，那么结果是什么呢将n的时间复杂度乘上一个log n也就是T(n)=O(n^log b a^ log n)

学习了主定理后，妈妈再也不用担心我的学习
证(wo)明(bu)略(hui)