AI大模型面试时被问到“Scaling Law”，怎么答？

前言

在大模型的研发中，通常会有下面一些需求：

• 计划训练一个 10B 的模型，想知道至少需要多大的数据？

• 收集到了 1T 的数据，想知道能训练一个多大的模型？

• 老板准备 1 个月后开发布会，给的资源是 100 张 A100，应该用多少数据训多大的模型效果最好？

• 老板对现在 10B 的模型不满意，想知道扩大到 100B 模型的效果能提升到多少？

以上这些问题都可以基于 Scaling Law 的理论进行回答。本文是阅读了一系列 Scaling Law 的文章后的整理和思考，包括 Scaling Law 的概念和推导以及反 Scaling Law 的场景，不当之处，欢迎指正。

1、核心结论

大模型的 Scaling Law 是 OpenAI 在 2020 年提出的概念，具体如下：

（1） 对于 Decoder-only 的模型，计算量 C(Flops), 模型参数量 N，数据大小 D(token 数)，三者满足：C≈6ND。(推导见本文最后)

（2） 模型的最终性能主要与计算量 C，模型参数量 N 和数据大小 D 三者相关，而与模型的具体结构(层数/深度/宽度)基本无关。

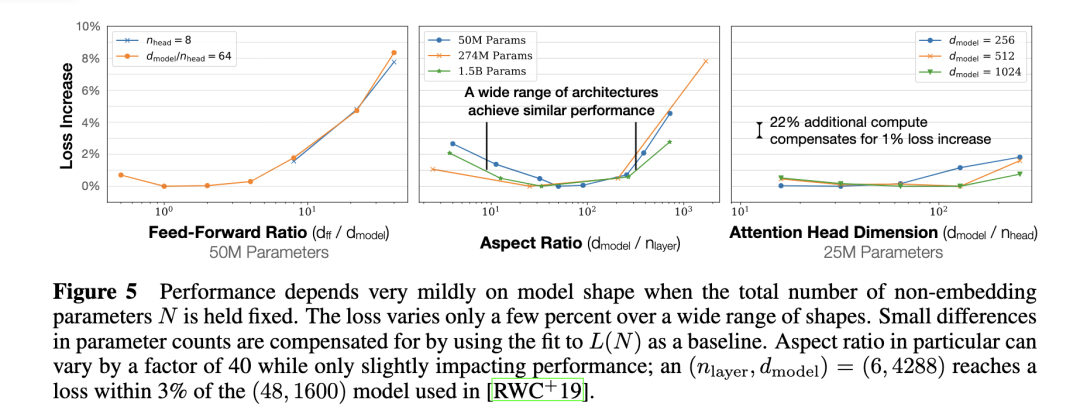
固定模型的总参数量，调整层数/深度/宽度，不同模型的性能差距很小，大部分在 2% 以内。

（3） 对于计算量 𝐶，模型参数量 𝑁 和数据大小 𝐷，当不受其他两个因素制约时，模型性能与每个因素都呈现幂律关系。

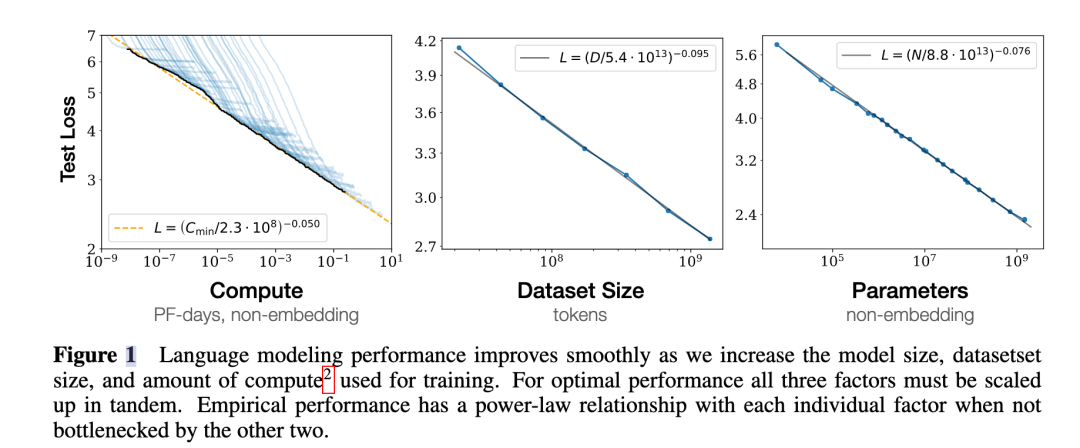
（4） 为了提升模型性能，模型参数量 N 和数据大小 D 需要同步放大，但模型和数据分别放大的比例还存在争议。

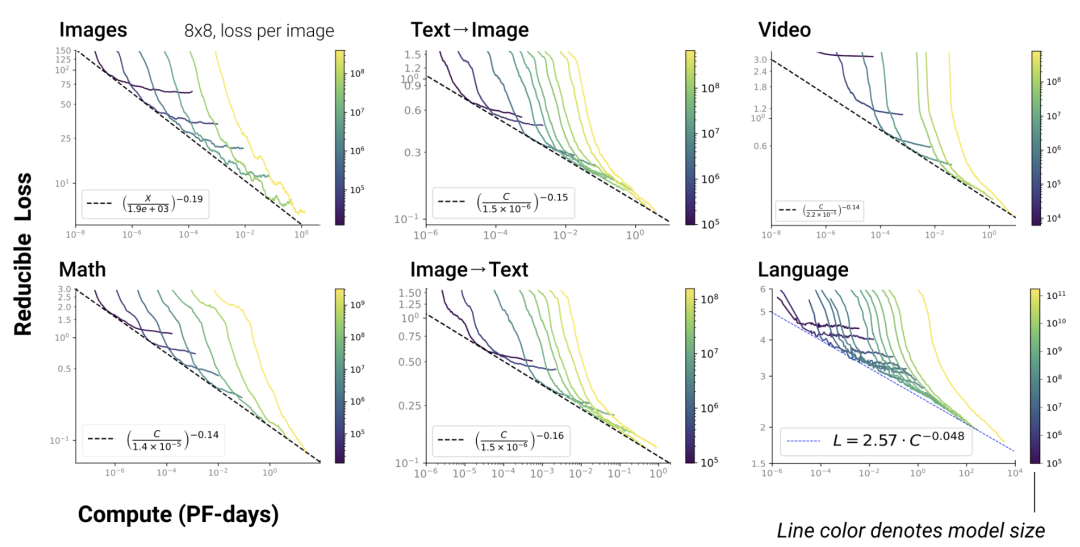
（5） Scaling Law 不仅适用于语言模型，还适用于其他模态以及跨模态的任务：

2、核心公式

如下图：

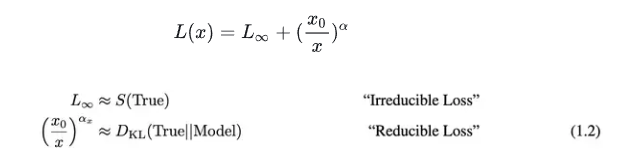
3、大模型中的Scaling Law

1.GPT4

下图是 GPT4 报告中的 Scaling Law 曲线，计算量 C 和模型性能满足幂律关系。

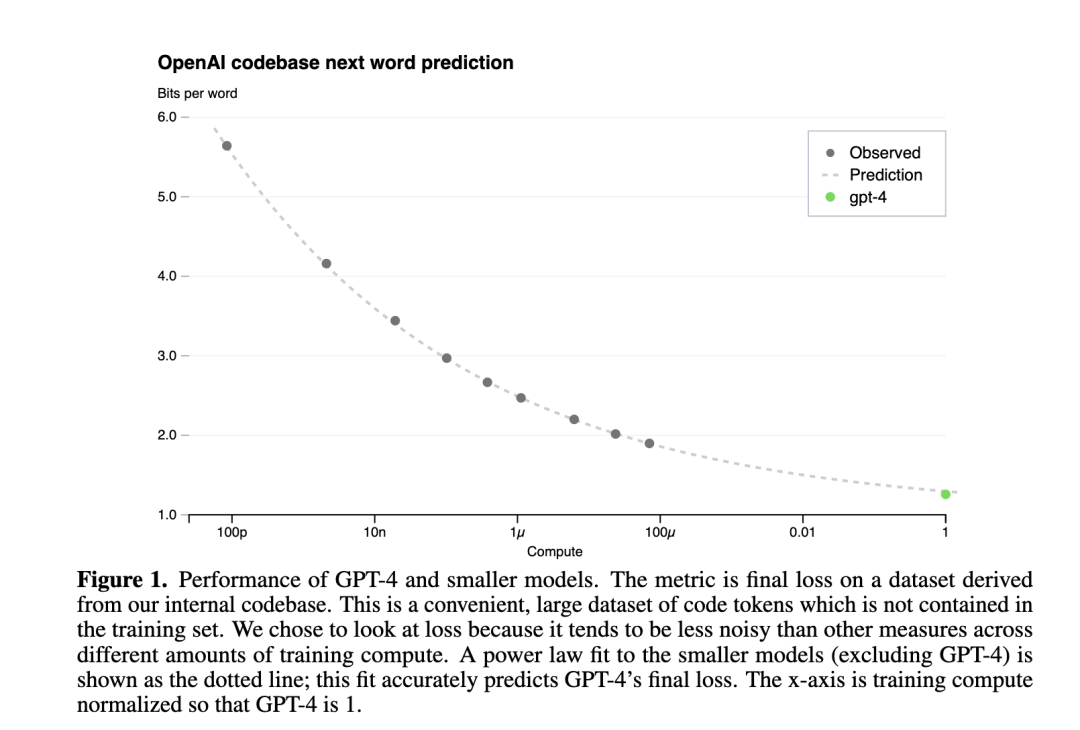
横轴是归一化之后的计算量，假设 GPT4 的计算量为 1。基于 10,000 倍小的计算规模，就能预测最终 GPT4 的性能。

纵轴是"Bits for words", 这也是交叉熵的一个单位。在计算交叉熵时，如果使用以 2 为底的对数，交叉熵的单位就是 “bits per word”，与信息论中的比特（bit）概念相符。所以这个值越低，说明模型的性能越好。

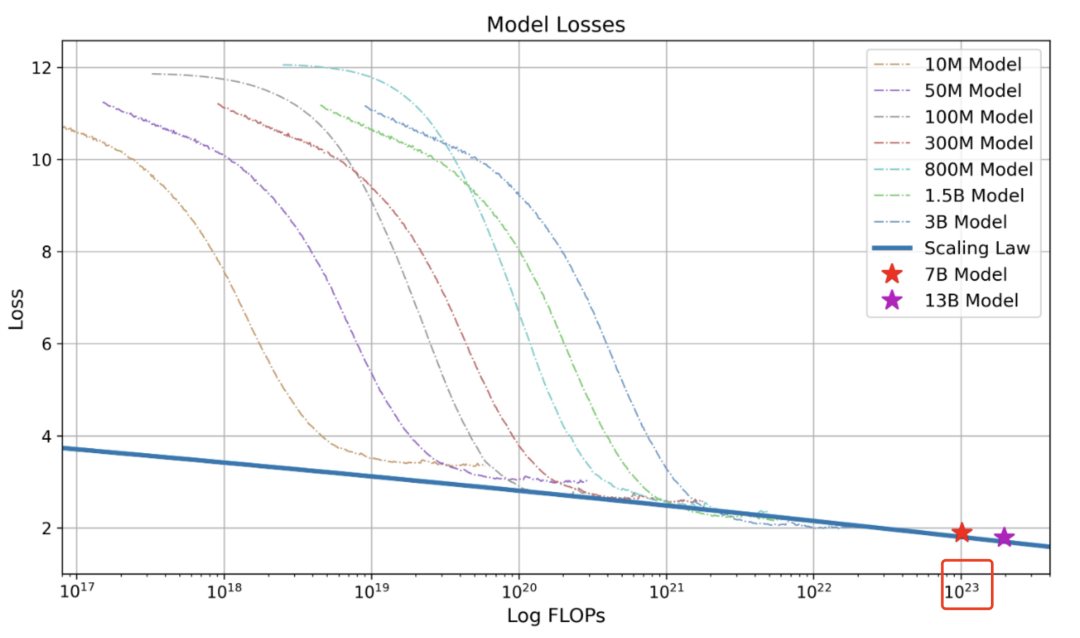
2.Baichuan2

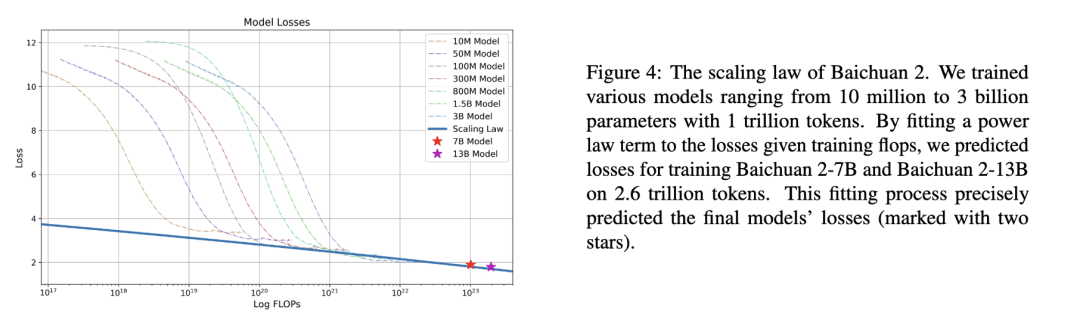
下图是 Baichuan2 技术报告中的 Scaling Law 曲线。基于 10M 到 3B 的模型在 1T 数据上训练的性能，可预测出最后 7B 模型和 13B 模型在 2.6T 数据上的性能。

3.MindLLM

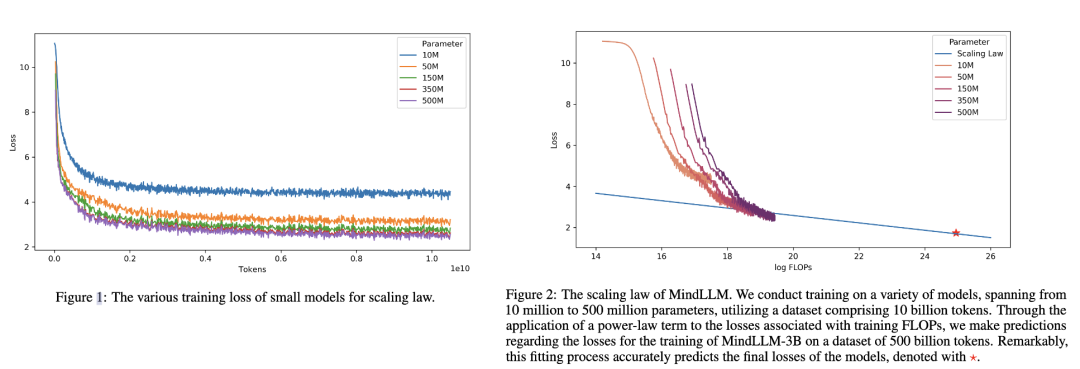
下图是 MindLLM 技术报告中的 Scaling Law 曲线。基于 10M 到 500M 的模型在 10B 数据上训练的性能，预测出最后 3B 模型在 500B 数据上的性能。

4、Scaling Law实操：计算效率最优

根据幂律定律，模型的参数固定，无限堆数据并不能无限提升模型的性能，模型最终性能会慢慢趋向一个固定的值。

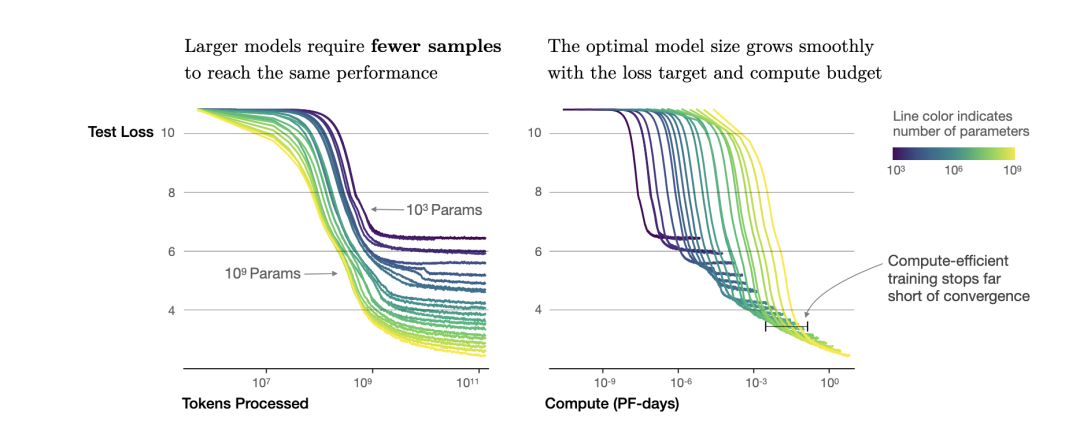
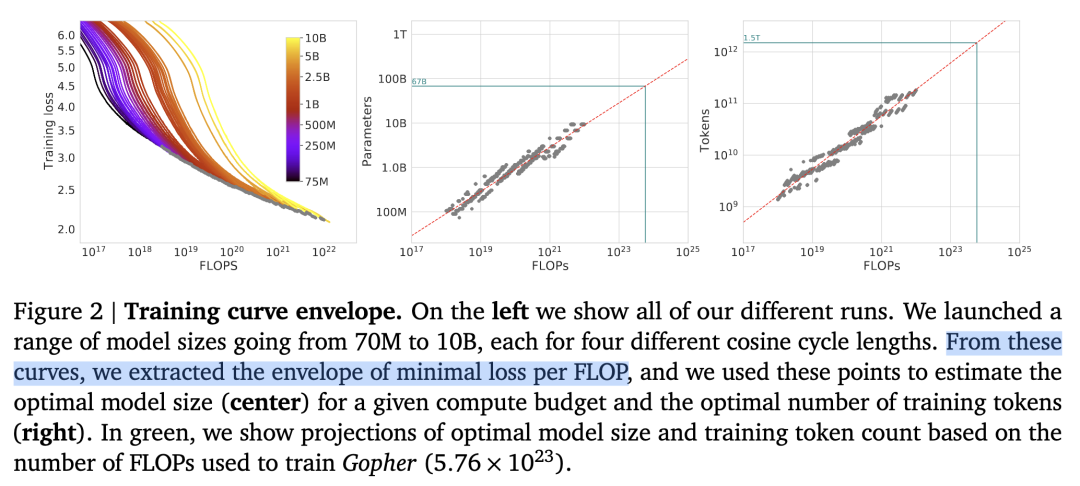
按照上面的思路，下面进行 Scaling Law 的实操。

首先准备充足的数据（例如 1T），设计不同模型参数量的小模型(例如 0.001B - 1B)，独立训练每个模型，每个模型都训练到基本收敛（假设数据量充足）。

根据训练中不同模型的参数和数据量的组合，收集计算量与模型性能的关系。

然后可以进一步获得计算效率最优时，即同样计算量下性能最好的模型规模和数据大小的组合，模型大小与计算量的关系，以及数据大小与计算量的关系。

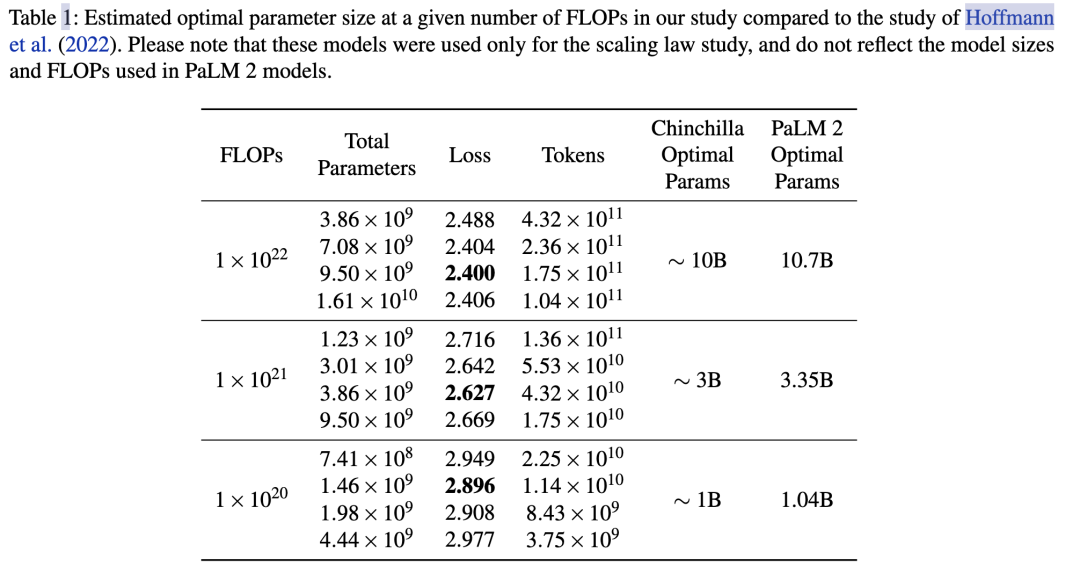
具体最好在自己的数据上做实验来获得你场景下的 a 和 b。

5、LLaMA：反Scaling Law的大模型

假设遵循计算效率最优来研发 LLM，那么根据 Scaling Law，给定模型大小，可以推算出最优的计算量，进一步根据最优计算量就能推算出需要的 token 数量，然后训练就行。

但是计算效率最优这个观点是针对训练阶段而言的，并不是推理阶段，实际应用中推理阶段效率更实用。

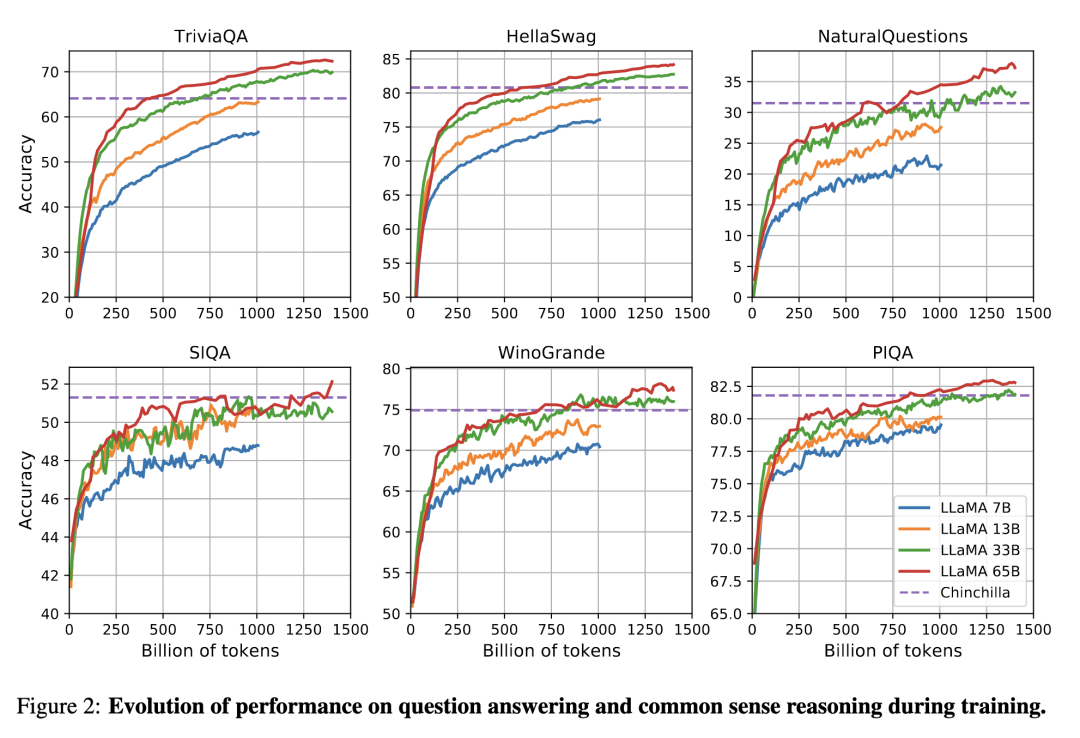
Meta 在 LLaMA 的观点是：给定模型的目标性能，并不需要用最优的计算效率在最快时间训练好模型，而应该在更大规模的数据上，训练一个相对更小模型，这样的模型在推理阶段的成本更低，尽管训练阶段的效率不是最优的（同样的算力其实能获得更优的模型，但是模型尺寸也会更大）。

根据 Scaling Law，10B 模型只需要 200B 的数据，但是作者发现 7B 的模型性能在 1T 的数据后还能继续提升。

所以 LLaMA 工作的重点是训练一系列语言模型，通过使用更多的数据，让模型在有限推理资源下有最佳的性能。

具体而言，确定模型尺寸后，Scaling Law 给到的只是最优的数据量，或者说是一个至少的数据量，实际在训练中观察在各个指标上的性能表现，只要还在继续增长，就可以持续增加训练数据。

6、计算量、模型和数据大小的关系推导

对于 Decoder-only 的模型，计算量C(Flops)，模型参数量 N(除去 Embedding 部分)，数据大小 D(token 数)，三者的关系为: C≈6ND。

推导如下，记模型的结构为：

继续推导模型的前向推理的计算量：

self-attention 部分的计算：

MLP 部分的计算：

最后的最后

感谢你们的阅读和喜欢，我收藏了很多技术干货，可以共享给喜欢我文章的朋友们，如果你肯花时间沉下心去学习，它们一定能帮到你。

因为这个行业不同于其他行业，知识体系实在是过于庞大，知识更新也非常快。作为一个普通人，无法全部学完，所以我们在提升技术的时候，首先需要明确一个目标，然后制定好完整的计划，同时找到好的学习方法，这样才能更快的提升自己。

这份完整版的大模型 AI 学习资料已经上传优快云，朋友们如果需要可以微信扫描下方优快云官方认证二维码免费领取【保证100%免费】

大模型知识脑图

为了成为更好的 AI大模型 开发者，这里为大家提供了总的路线图。它的用处就在于，你可以按照上面的知识点去找对应的学习资源，保证自己学得较为全面。

经典书籍阅读

阅读AI大模型经典书籍可以帮助读者提高技术水平，开拓视野，掌握核心技术，提高解决问题的能力，同时也可以借鉴他人的经验。对于想要深入学习AI大模型开发的读者来说，阅读经典书籍是非常有必要的。

实战案例

光学理论是没用的，要学会跟着一起敲，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。

面试资料

我们学习AI大模型必然是想找到高薪的工作，下面这些面试题都是总结当前最新、最热、最高频的面试题，并且每道题都有详细的答案，面试前刷完这套面试题资料，小小offer，不在话下

640套AI大模型报告合集

这套包含640份报告的合集，涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师，还是对AI大模型感兴趣的爱好者，这套报告合集都将为您提供宝贵的信息和启示。

这份完整版的大模型 AI 学习资料已经上传优快云，朋友们如果需要可以微信扫描下方优快云官方认证二维码免费领取【保证100%免费】