大模型必备知识：量化加速

最新推荐文章于 2025-12-08 09:09:42 发布

原创最新推荐文章于 2025-12-08 09:09:42 发布 · 656 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #人工智能 #深度学习 #神经网络 #语言模型 #边缘计算

从零开始一步步构建大模型专栏收录该内容

10 篇文章

订阅专栏

模型量化原理（Part 1）：数值表示与线性映射

模型量化的本质，是在精度与效率之间做权衡。简单来说，就是把高精度的浮点数映射到低精度的整数空间中。以Llama13B为例，如果用FLOAT32来加载，参数要占52GB，如果用FLOAT16来加载，需要26GB，用int8仅需要13GB.

要理解量化，首先必须理解计算机是如何存储数字的。

在深度学习模型（如 PyTorch 的默认设置）中，权重和激活值通常使用 FP32（32-bit Floating Point）。

1.1 IEEE 754 标准（FP32 的代价）

一个 FP32 数值在内存中占用 32 个比特，其结构如下：

$V = (-1)^S \times (1.M) \times 2^{E - 127}$

Sign ( $S$ , 1 bit): 符号位。
Exponent (E, 8 bits): 指数位，决定数值的动态范围（Range）。
Mantissa (M, 23 bits): 尾数位，决定数值的精度（Resolution）。

为什么 FP32 运算昂贵？

当你做一次 FP32 加法时，CPU/GPU 内部的浮点运算单元（FPU）需要做以下复杂操作：

对阶（Alignment）： 比较两个数的指数，把较小的数的尾数右移。
尾数计算： 进行加减。
规格化（Normalization）： 调整结果，使其符合 1.M的格式。
舍入（Rounding）： 处理溢出的比特。

这不仅占内存（4 Bytes），而且能耗高、芯片面积大。

1.2 INT8（8-bit Integer）的优势

相比之下，INT8 只占用 1 个字节（8 bits），范围固定在 $[-128, 127]$ （有符号）或 $[0, 255]$ （无符号）。

内存带宽： 减少 4 倍（32 bit $\to$ 8 bit），这是大模型推理最关键的瓶颈（Memory Wall）。
计算效率： 整数加法极其简单，不需要对阶和归一化。现在的 GPU（如 NVIDIA Tensor Core）计算 INT8 的吞吐量（TOPS）通常是 FP32 的数倍。

2. 核心数学原理：仿射量化（Affine Quantization）

量化的核心任务，就是建立一个从实数域（Real Domain, FP32）到整数域（Integer Domain, INT8）的数学映射。

目前工业界（如 TensorRT, PyTorch, TensorFlow Lite）最通用的标准是线性量化（Linear Quantization），也称为仿射量化。

2.1 映射公式

想象我们有一把尺子。

FP32 空间是连续的（或者非常密集），范围可能是 $[-3.5, 2.5]$ 。
INT8 空间是离散的网格，只有 256 个刻度。

我们要把 FP32 的数值 $r$ （real）映射到 INT8 的数值 $q$ （quantized）。公式如下：

$q = \text{clamp}(\text{round}(\frac{r}{S} + Z), q_{min}, q_{max})$

相应的反量化（Dequantization）公式（用于恢复数值进行计算或输出）是：

$r \approx S \times (q - Z)$

2.2 关键参数详解

这个公式中有两个至关重要的参数，量化算法的核心就是如何确定这两个参数：

Scale ($S$, 缩放因子):
- 物理意义： 它是 FP32 空间中两个相邻 INT8 刻度之间的距离。它决定了量化的粒度。
- 类型： $S$ 通常是一个 FP32 浮点数。
- 公式：
  
  $S = \frac{r_{max} - r_{min}}{q_{max} - q_{min}}$
  
  其中 $r_{max}, r_{min}$ 是待量化张量（Tensor）中的最大值和最小值。
Zero Point (Z, 零点):
- 物理意义： FP32 中的 $0.0$ 对应到 INT8 中的哪个整数？
- 为什么需要它？ 神经网络中大量的计算涉及 Zero Padding（补零）或者 ReLU（输出为 0）。如果 FP32 的 $0.0$ 量化后有误差（例如变成了 INT8 的 1），那么原本无意义的 Padding 区域就会变成非零值，导致巨大的累积误差。
- 约束： $Z$ 必须是一个整数，这样才能保证 $0.0$ 被精确地表示为整数，没有任何量化误差。
- 公式：
  
  $Z = \text{round}(q_{min} - \frac{r_{min}}{S})$

让我们忘掉公式，换一个非常直观的生活案例来理解。

1. 直观类比：尺子与刻度

想象你有一根非常精准的尺子（FP32，浮点数），它可以测量出 1.23456 厘米、5.67891 厘米。现在，不管是出于省钱（节省内存）还是为了便于携带（计算更快），你被强迫换成一根只有整数刻度的小学生尺子（INT8），这把尺子只有 0, 1, 2, ..., 255 这几个刻度。

现在的任务是：

怎么用这把**“整数尺子”去表示原本那些“精准的数字”**？

我们需要做两个决定：

缩放（Scale, S）： 整数尺子上的一格（比如从 1 到 2），代表真实世界里的多少厘米？
零点（Zero Point, Z）： 整数尺子上的“0”刻度，对应真实世界的多少厘米？（因为真实世界可能有负数，而我们的尺子是从 0 开始的）。

2. 手把手算一次

为了让你彻底明白，我们不做抽象推导，直接手动算这 3 个数。

假设模型的某一层只有 3 个权重参数（FP32）：

数据： [-1.0, 0.0, 1.0]

我们要把它们塞进 INT8 的范围：[0, 255]。

第一步：找范围（Range）

真实数据的最小值 $r_{min} = -1.0$
真实数据的最大值 $r_{max} = 1.0$
真实数据的总跨度 = $1.0 - (-1.0) = 2.0$

第二步：定步长（Scale,S）

我们的 INT8 尺子一共有 255 个格子（从 0 到 255）。

我们要把总跨度 2.0 平均分到这 255 个格子里。

$S = \frac{\text{REAL}}{\text{INT}} = \frac{2.0}{255} \approx 0.007843$

这意味着：INT8 里的数值每增加 1，代表真实数值增加了 0.007843。

第三步：定零点（Zero Point, Z）

现在我们要找对齐点。

真实世界的 $r_{min} (-1.0)$ 必须对应 INT8 的最小值 $0$ 。

那么，真实世界的 $0.0$ 应该对应 INT8 的多少呢？

从 $-1.0$ 到 $0.0$ ，真实距离走了 $1.0$ 。
一步长是 $0.007843$ 。
需要走的步数 = $1.0 / 0.007843 \approx 127.5$ 。

因为 INT8 必须是整数，我们要四舍五入。所以 $Z = 128$ 。

这意味着：INT8 中的数字 128，代表真实世界的 0.0。

第四步：开始转换（量化）

现在我们有了 $S \approx 0.0078$ 和 $Z = 128$ 。公式就是：

$INT = \text{round}(\frac{\text{REAL}}{S} + Z)$

我们来看看那三个数变成了什么：

-1.0 $\rightarrow$ $(-1.0 / 0.0078) + 128 = -127.5 + 128 = 0.5 \rightarrow$ 0 (对应 INT8 最小值)
0.0 $\rightarrow$ $(0.0 / 0.0078) + 128 = 0 + 128 = 128 \rightarrow$ 128
1.0 $\rightarrow$ $(1.0 / 0.0078) + 128 = 127.5 + 128 = 255.5 \rightarrow$ 255 (对应 INT8 最大值)

结果：

原本的浮点数组 [-1.0, 0.0, 1.0] 被压缩成了整数数组 [0, 128, 255]。

这就完成了量化！

3. 反量化（还原）与误差

当我们推理时，需要把整数还原回去（或者在整数域计算完后还原）。

公式： $REAL \approx S \times (INT - Z)$

让我们看看还原回去变成了多少：

0 $\rightarrow$ $0.007843 \times (0 - 128) = -1.0039$
128 $\rightarrow$ $0.007843 \times (128 - 128) = 0.0$
255 $\rightarrow$ $0.007843 \times (255 - 128) = 0.996$

请注意误差：

原始值：-1.0 vs 还原值：-1.0039
原始值：1.0 vs 还原值：0.996

这种微小的差别就是量化误差（Quantization Error）。这也是为什么量化模型精度通常会稍微下降一点点的原因。

3. 对称量化 vs. 非对称量化

根据 $Z$ 是否强制为 0，量化策略分为两种：

3.1 非对称量化 (Asymmetric Quantization)

定义： $Z \neq 0$ 。
特点： 能够充分利用 INT8 的整个范围 $[0, 255]$ 或 $[-128, 127]$ 来覆盖数据的实际分布。
适用场景： 数据分布不关于原点对称的情况。例如 ReLU 激活后的输出，其值域是 $[0, +\infty)$ ，全是正数。如果强行把 $0$ 放在 INT8 的中间，就会浪费一半的比特位。

3.2 对称量化 (Symmetric Quantization)

定义： 强制 $Z = 0$ 。
特点： 映射公式简化为 $r = S \times q$ 。
优势： 计算速度更快（后面讲矩阵乘法原理时会提到，因为少了一个 $Z$ 项，计算复杂度降低）。
适用场景： 数据分布大致关于 0 对称的情况。例如 模型权重（Weights） 通常分布在 0 附近。
注意： 对于对称量化，为了保证 0 点对齐，我们通常选取 $r_{max} = \max(|r_{min}|, |r_{max}|)$ ，范围设为 $[-r_{max}, r_{max}]$ 。

到目前为止，我们建立了一个静态的映射视角：

量化就是把连续的信号 r，除以步长 S，加上偏移 Z，再四舍五入到最近的整数格子上。

但是，深度学习不仅仅是存储数据，更重要的是运算（主要是矩阵乘法）。

如果只是把权重变成了 INT8，但计算时还要转回 FP32，那这就仅仅节省了显存，并没有加速计算。
真正的加速来自于直接在 INT8 格式下进行矩阵乘法。

模型量化原理（Part 2）：量化矩阵乘法与加速机制

在第一部分，我们学会了如何把实数存成整数。但如果我们在计算时，把 INT8 转回 FP32 再算矩阵乘法（Matrix Multiplication），那我们只是节省了显存，并没有节省计算时间，甚至因为频繁的类型转换（Cast）导致变慢。

真正的量化加速，必须在整数域（Integer Domain）直接进行矩阵乘法。

我们将从数学推导出发，拆解计算机是如何“骗”过浮点运算单元，直接用整数算出结果的。

1. 为什么整数运算更快？（体系结构视角）

在深入公式前，先看硬件底层的物理差距。

假设你要算 $A \times B + C$ 。

FP32 运算： 需要巨大的浮点运算单元（FPU），处理指数对齐、尾数相乘、规格化。
INT8 运算： 只需要简单的整数算术逻辑单元（ALU）。

NVIDIA GPU (以 A100 为例) 的算力对比：

FP32 Tensor Core: 156 TFLOPS
INT8 Tensor Core: 624 TOPS (Tera Operations Per Second)
差距： 理论上有 4倍的性能提升。

为了吃到这就这 4 倍的红利，我们必须推导出全整数的矩阵乘法公式。

2. 量化矩阵乘法（GEMM）的数学推导

我们要计算全连接层或卷积层的核心操作：两个数值的点积（Dot Product）。

$y = \sum_{i=1}^{N} w_i x_i$

其中：

$w_i$ : 权重（Weights），浮点数。
$x_i$ : 输入激活值（Activations），浮点数。
$y$ : 输出结果，浮点数。

2.1 引入量化公式

根据 Part 1 的公式 $r = S(q - Z)$ ，我们将 $w$ 和 $x$ 替换为它们的量化形式：

$w_i = S_w (q_{w,i} - Z_w)$

$x_i = S_x (q_{x,i} - Z_x)$

代入点积公式：

$y = \sum_{i=1}^{N} [S_w (q_{w,i} - Z_w)] \cdot [S_x (q_{x,i} - Z_x)]$

2.2 提取常数项

由于 $S_w$ （权重的缩放因子）和 $S_x$ （输入的缩放因子）对于这一层的所有元素都是常数（假设是 Per-Tensor 量化），我们可以把它们提出来：

$y = S_w S_x \sum_{i=1}^{N} (q_{w,i} - Z_w)(q_{x,i} - Z_x)$

2.3 展开多项式（关键步骤！）

利用求和符号的线性性质，我们可以把它拆成四部分：

3. 逐项分析与优化策略

让我们看看这四个项在计算机里是怎么处理的，为什么它能变快？

3.1 项1： $\sum q_{w,i} q_{x,i}$

含义： 这是两个 INT8 矩阵的直接乘法。
计算： 这是计算量最大的部分（占 99% 以上）。
加速： 现代 GPU（如 Tensor Core）和 CPU（如 AVX-512 VNNI 指令集）有专门的硬件指令，可以在一个时钟周期内完成大量的 INT8 $\times$ INT8 $\to$ INT32 运算。

3.2 项3： $Z_x \sum q_{w,i}$

含义： 权重的零点 $\times$ 权重的和。
优化（重点）：注意，权重 $q_w$ 在模型训练好之后就是固定的！

这意味着 $\sum q_{w,i}$ 可以提前算出（Pre-computed）。

在推理阶段，这一项只是一个单纯的数字，不需要实时计算。直接查表读取即可。

3.3 项4： $N Z_w Z_x$

含义： 纯常数。
优化： 同样可以提前算出。

3.4 项2： $Z_w \sum q_{x,i}$

含义： 权重的零点 $\times$ 输入的和。
计算： 输入 $x$ 是动态变化的，所以这一项必须实时计算。
代价： 这是一个简单的求和操作，计算复杂度为 $O(N)$ ，远小于矩阵乘法的 $O(N^2)$ 或 $O(N^3)$ ，所以开销可以忽略不计。

4. 为什么大家喜欢“对称量化”？

回顾 Part 1，对称量化（Symmetric Quantization） 强制 $Z = 0$ 。

如果我们让权重 $W$ 使用对称量化，即 $Z_w = 0$ ，上面的公式会发生什么变化？

项2 ( $Z_w \sum q_x$ ) 变为 0。
项4 ( $N Z_w Z_x$ ) 变为 0。

公式瞬间简化为：

$y = S_w S_x [ \sum_{i=1}^{N} q_{w,i} q_{x,i} - Z_x \sum_{i=1}^{N} q_{w,i} ]$

如果输入 $X$ 也使用对称量化（ $Z_x = 0$ ），公式进一步简化为：

$y = S_w S_x \sum_{i=1}^{N} q_{w,i} q_{x,i}$

这就是为什么 NVIDIA 的 TensorRT 极力推荐对称量化：

它消除了所有额外的加减法操作，只保留了最高效的矩阵乘法核心。

5. 累加器（Accumulator）与位宽溢出

这里有一个工程实现的陷阱。

我们输入的 $q_w$ 和 $q_x$ 都是 INT8（8-bit）。

$q_w \times q_x$ 的结果最大可能是 $255 \times 255 \approx 65,025$ ，这需要 16-bit (INT16) 来存储。
但是，一个矩阵乘法通常涉及成千上万次加法（ $\sum_{i=1}^{N}$ ）。
如果我们把这些 INT16 的乘积加起来，结果会迅速超过 65,535，导致 INT16 溢出。

解决方案：INT32 累加器 在硬件底层（如 Tensor Core）：

输入： 两个 INT8 矩阵。
乘法： 结果暂存为 INT16（或直接进入 INT32）。
加法（Accumulation）： 必须在一个 INT32（32-bit Integer） 的寄存器中进行累加。INT32 最大可以表示 20 亿左右的数字，足以防止溢出。

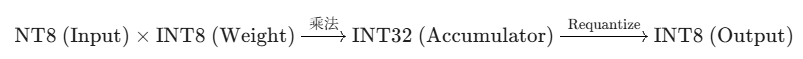
注意最后一步：累加完的结果是 INT32，但下一层的输入需要 INT8。所以我们需要把这个 INT32 的结果再次量化（Requantize）回 INT8。

这部分的很多概念是高性能计算（HPC）的核心。我们学到了：

量化 GEMM 公式： 通过数学展开，将浮点点积转化为整数点积 + 修正项。
预计算（Pre-computation）： 凡是和权重 W相关的项，都可以在离线阶段算好，推理时直接加，这是提速的关键。
对称量化的优势： 通过令 Z=0，消除修正项，进一步榨干硬件性能。
INT32 累加器： 为了防止求和溢出，中间结果必须用高精度整数存储。

到目前为止，我们解决了“怎么存”（Part 1）和“怎么算”（Part 2）。

还有最后一个大问题（Part 3）：

我们一直假设 S（Scale）和 Z（Zero Point）是已知的。

但在实际应用中，对于一个拥有几十亿参数的大模型，这里的 S 和 Z$到底是怎么确定的？

是每一层用一套参数？还是每一个通道用一套？（粒度问题）
如何保证量化后精度损失最小？（校准 Calibration 问题）
如何处理像 Transformer 中的 LayerNorm 或 Softmax 这种非线性层？

模型量化原理（Part 3）：粒度与校准

1. 量化粒度（Granularity）：一把尺子还是一组尺子？

在计算 Scale ( $S$ ) 时，我们是基于多大范围的数据来统计 $r_{max}$ 和 $r_{min}$ 的？这就叫粒度。

1.1 Per-Tensor Quantization（层级量化）

做法： 整个张量（比如一整层的权重矩阵 W）共用一个 S和 Z。
优点： 简单，内存占用最少。
致命缺陷： “姚明问题”。
- 假设一个权重矩阵里，绝大多数数值都在 [-0.1, 0.1] 之间。
- 突然出现了一个巨大的离群值（Outlier），比如 100.0（姚明）。
- 为了包容这个 100.0，你的 Scale S 会变得很大（ $S \approx 100/255$ ）。
- 结果：原本那些 $[-0.1, 0.1]$ 的细节数值，除以巨大的 $S$ 后，全部变成了 $0$ 。
- 后果： 整个层的参数信息丢失殆尽，模型失效。

1.2 Per-Channel Quantization（通道级量化）

这是 CNN 和 Transformer 中最常用的方案。

做法： 对权重矩阵的每一个输出通道（Output Channel），单独计算一组 S和 Z。
- 如果有 512 个通道，就会有 512 个 $S$ 和 512 个 $Z$ 。
原理： 即使第 1 个通道里有“姚明”，导致该通道量化很粗糙；但第 2 个通道里全是普通人，可以用很精细的 Scale 来保留精度。各通道互不干扰。
计算代价：
- 回顾矩阵乘法公式： $y = S_w S_x (\dots)$ 。
- 如果是 Per-Channel，这里的 $S_w$ 变成了一个向量 $S_{w, i}$ 。
- 巧妙的是，由于矩阵乘法的性质，输出的每一行本来就是独立计算的，所以给每一行乘上不同的 Scaling Factor 并不会打断流水线，几乎零开销。

工业界结论： 权重（Weights）必须使用 Per-Channel 量化，否则精度损失无法接受。激活值（Activations）通常使用 Per-Tensor 量化（为了硬件计算效率）。

2. 激活值的校准（Calibration）：如何预测未来？

权重是静态的，我们在部署前就能看到所有权重，算出完美的 Max/Min。

激活值（输入/输出）是动态的，随着用户的输入图片/文本不同而剧烈变化。

我们如何确定激活值的 $r_{max}$ 和 $r_{min}$ ？

2.1 动态量化 (Dynamic Quantization)

做法： 模型运行时，每来一个输入 x，先统计一遍它的 max/min，实时计算 S 和 Z，再进行量化计算。
优点： 精度最高，自适应性强。
缺点： 慢！每次都要实时统计，这在计算图里增加了额外的 overhead。

2.2 静态量化 (Static Quantization / PTQ)

做法：
1. 准备校准集（Calibration Set）： 找 100 张典型的图片或一段文本。
2. 跑模型： 用 FP32 模式跑一遍，收集每一层激活值的统计分布（Histogram）。
3. 定参数： 根据统计结果，永久固定住 S 和 Z。
4. 部署： 推理时不再重新计算 Scale。
难点： 如果校准集里没出现过“极端情况”，部署时遇到了怎么办？（通常截断 Clamping）。

3. 截断策略：为了大局，牺牲局部

在静态量化中，如何根据统计直方图确定 $r_{max}$ ？

这并不像“找最大值”那么简单。

3.1 MinMax 策略

做法： 直接取直方图中的绝对最大值。 $r_{max} = \max(|x|)$ 。
问题： 极度敏感。只要校准集里有一个噪点（Outlier），Scale 就会被拉大，导致整体精度下降。

3.2 移动平均 MinMax (Moving Average MinMax)

做法： 在校准过程中，对每个 Batch 的 Min/Max 做指数移动平均。
特点： PyTorch 默认方法，比单纯 MinMax 稳定一点。

3.3 KL 散度（KL Divergence / Entropy Calibration）

这是 NVIDIA TensorRT 的默认方法，也是基于信息论的高级策略。

核心思想： 我们不关心绝对数值的还原，我们关心的是信息量的损失最小化。
步骤：
1. 拿到 FP32 的激活值分布 P（比如 2048 个桶的直方图）。
2. 尝试不同的截断阈值 T（比如截掉最外侧的 10% 数据）。
3. 把截断后的数据量化成 INT8 分布 Q（128 个桶）。
4. 计算 P 和 Q 之间的 KL 散度（Kullback-Leibler Divergence）：
  
  $D_{KL}(P || Q) = \sum P(i) \log \frac{P(i)}{Q(i)}$
5. 选取让 KL 散度最小的那个阈值 T作为 $r_{max}$ 。
直觉： 哪怕截断了一部分很大的离群值（Clip），只要剩下的部分能更精细地描述主要数据分布，模型的最终效果反而更好。

4. 终极武器：量化感知训练 (QAT)

如果上述所有方法（PTQ, Post-Training Quantization）用完后，模型精度还是掉得厉害（比如下降了 5%），怎么办？

这时候只能祭出 QAT (Quantization Aware Training)。

4.1 核心思想

在训练阶段（Training），就提前让模型“感受”到量化的痛苦。

我们在计算图中插入“伪量化节点”（Fake Quantization Nodes）：

$x_{fake} = \text{dequantize}(\text{quantize}(x))$

这个节点会模拟 $FP32 \to INT8 \to FP32$ 的过程，人为引入量化噪声。

4.2 梯度的悖论与 STE

但在反向传播（Backpropagation）时，有一个数学难题：

量化函数（Round）是阶梯状的。

在台阶面上，导数为 0。
在跳变点，导数无穷大。
结论： 梯度没法传导，网络无法训练。

解决方案：直通估计器 (Straight Through Estimator, STE)

我们“欺骗”链式法则。

前向传播时： 严格执行四舍五入 $x_{out} = \text{round}(x_{in})$ 。
反向传播时： 假设这个函数是恒等映射 $y=x$ ，即 $\frac{\partial L}{\partial x_{in}} = \frac{\partial L}{\partial x_{out}}$ 。直接把梯度原封不动地传过去。