深度强化学习-Actor-Critic（演员-评论家）算法详解：从基础理念到 A3C 演进

原创已于 2025-11-15 16:58:43 修改 · 916 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #人工智能 #深度学习 #机器学习 #数据分析

于 2025-11-15 16:50:45 首次发布

深度强化学习DRL 专栏收录该内容

5 篇文章

订阅专栏

在深度强化学习的世界里，许多初学者会被一上来的一堆概念搞懵：Q-learning、策略梯度、Actor-Critic、A3C、PPO……仿佛每一个都很重要，但似乎每一个都很难。

但如果你想真正理解现代强化学习的核心思想，Actor-Critic 是一条必须走通的主线：

理解 Actor（演员）＝理解策略方法（Policy-based）
理解 Critic（评论家）＝理解价值方法（Value-based）
理解 Actor-Critic ＝理解为什么许多最强的 RL 算法（A3C、PPO、SAC）都围绕这套框架展开

这篇文章的目标是：用生活化类比解释核心概念，用直觉讲明白原理，用一篇文章让你几乎打通 Actor-Critic 的基础和深层思维。

无复杂公式，少术语堆砌，但深刻。

一、了解 Actor-Critic

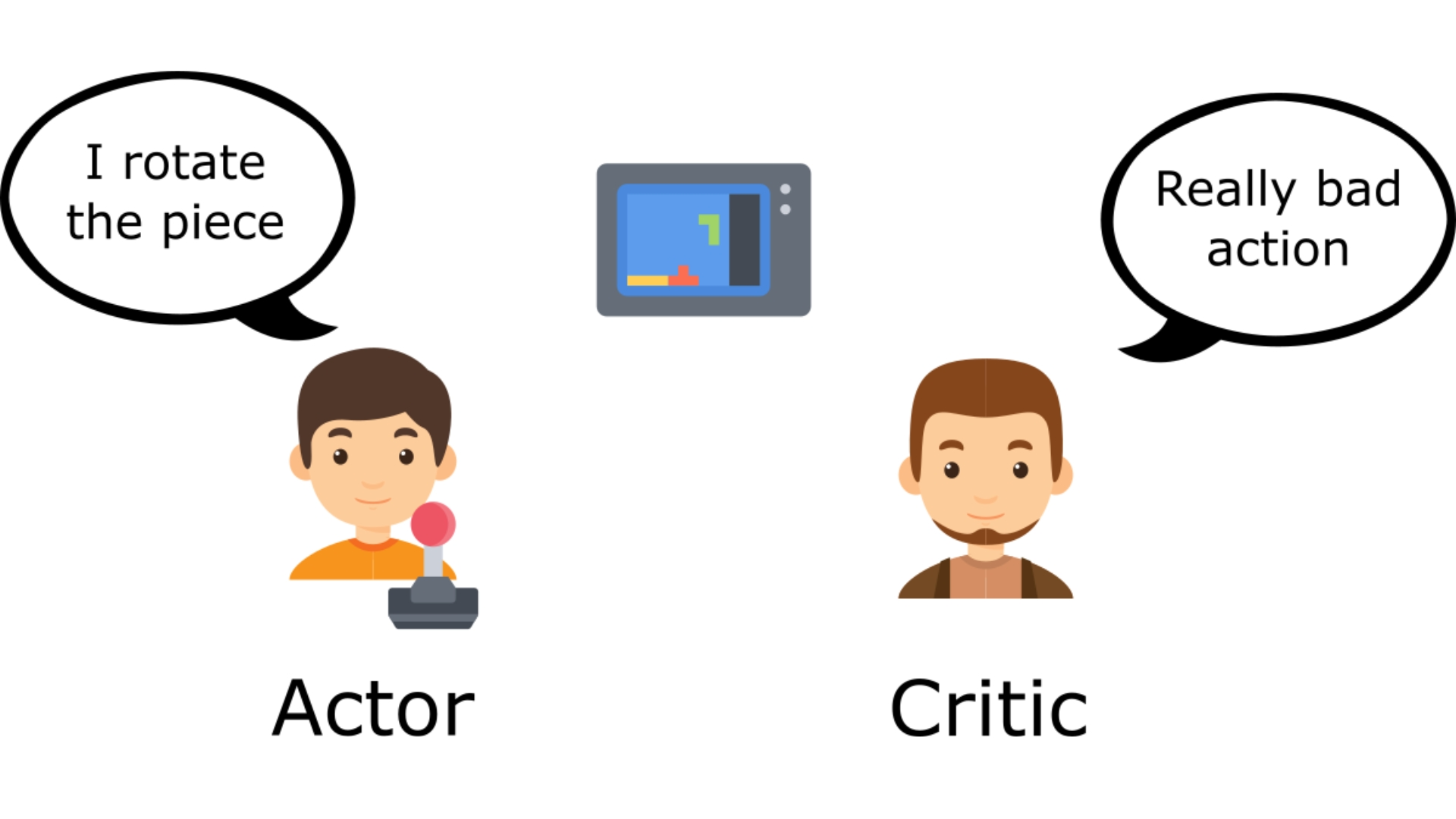
强化学习有两大类方法：

价值方法（Value-based）：如 Q-learning、DQN
只计算某个状态或动作的“好坏分数”
策略方法（Policy-based）：如 REINFORCE
直接学习如何做动作（策略 π），但学习波动大

它们各有优缺点，谁也不能独当一面。

Actor-Critic 的出现，就是为了结合两者的优势——既学会“该怎么做”，又学会“这一步到底好不好”。

通俗地说：

价值方法是“评分系统”，策略方法是“行为系统”。
Actor-Critic 是“行为系统 + 评分系统 = 高效、稳定的学习”。

1. 盲目的演员 (Policy-Based)

基于策略的方法（Policy-Based, PG）的核心思想很简单：好的奖励，就多做；坏的奖励，就少做。

以 REINFORCE 算法为例，它的更新逻辑是：

演员 (Actor) 在一个“回合”（Episode）中表演完一整套动作。
最后，它拿到了一个总奖励 $G_t$ （比如游戏得分100分）。
它回头看：“哇，我得了100分！看来我这一整套动作都挺不错的，我要增加做这些动作的概率。”

问题出在哪里？

这个问题就是“高方差 (High Variance)”。

奖励的“归功”不明确： 假设你在游戏中做了100个动作，最后赢了。你真的知道是哪几个动作导致了胜利吗？REINFORCE 算法粗暴地认为“所有动作都有功劳”，这显然不公平。也许第10个动作是神来之笔，而第50个动作其实很糟糕，只是被“平均”掉了。
奖励信号极其稀疏： 演员必须演完“一整出戏”才能得到一次“掌声”（奖励）。如果这出戏很长（比如一盘围棋），它可能要等几百步才知道自己做得好不好。在这之前，它完全是“盲目”的。
极其依赖采样： 你的“演员”这次运气好，碰巧赢了，它就强化了这套动作。下次运气不好，输了，它又去否定这套动作。策略的更新会非常不稳定，来回摇摆。

困境小结： “演员” (Policy-Based) 知道如何做动作，但它不知道“好坏的标准”，只能等最后的结果，导致学习效率低下且不稳定。

2. 只会计算的评论家 (Value-Based)

基于价值的方法（Value-Based）如 Q-Learning 或 DQN，则完全是另一个思路。

它不直接学习“该做什么动作” (策略 $\pi$ )，它学习一个“评论家” (Critic)，这个评论家专门给“在某个状态 s下，做某个动作 a” 这件事打分，这个分数叫 Q(s, a)。

它的核心思想是：我不需要知道策略是什么，我只要知道所有“状态-动作对”的价值，那我自然就知道最好的策略 —— 选 Q 值最高的那个动作就行了。

问题又出在哪里？

无法处理“连续动作”： 这是它最大的硬伤。DQN 的核心是“在所有可能的动作中，选一个Q值最大的”。如果动作是连续的（比如自动驾驶的方向盘转角、机器人的手臂力度），你根本无法“遍历所有动作”。
策略的“确定性”： DQN 选出来的策略是“确定性”的（Greedy）。在某个状态，它永远只会选那个最好的动作。但在很多现实场景中（比如石头剪刀布），“确定性”的策略是致命的，你一定需要“随机性”的策略。

困境小结： “评论家” (Value-Based) 擅长评估价值，但它“不会演戏”。它无法输出策略，也处理不了连续的动作空间。

3. Actor-Critic 的诞生

现在，我们把两个“和尚”的困境放在一起：

演员 (Actor): 会演戏（输出策略 $\pi(a|s)$ ），能处理连续动作，但需要一个“即时”的指导，而不是等到“剧终”才给个总分。
评论家 (Critic): 会打分（评估价值 $V(s)$ 或 $Q(s, a)$ ），能提供“即时”的反馈，但它自己不会演戏。

答案呼之欲出。

为什么我们不让“评论家”来指导“演员”呢？

这就是 Actor-Critic (AC) 算法的精髓：

我们同时训练两个网络。
演员 (Actor)：一个策略网络，负责输出动作（或动作的概率）。
评论家 (Critic)：一个价值网络，负责评估状态（比如 V(s)，即“当前状态有多好”）。

整个流程是这样的：

1.在每个时间步 t，我们从环境中获取当前状态 S_t，并将其作为输入传递给我们的 Actor 和 Critic。
我们的策略接收状态并输出一个动作 A_t。

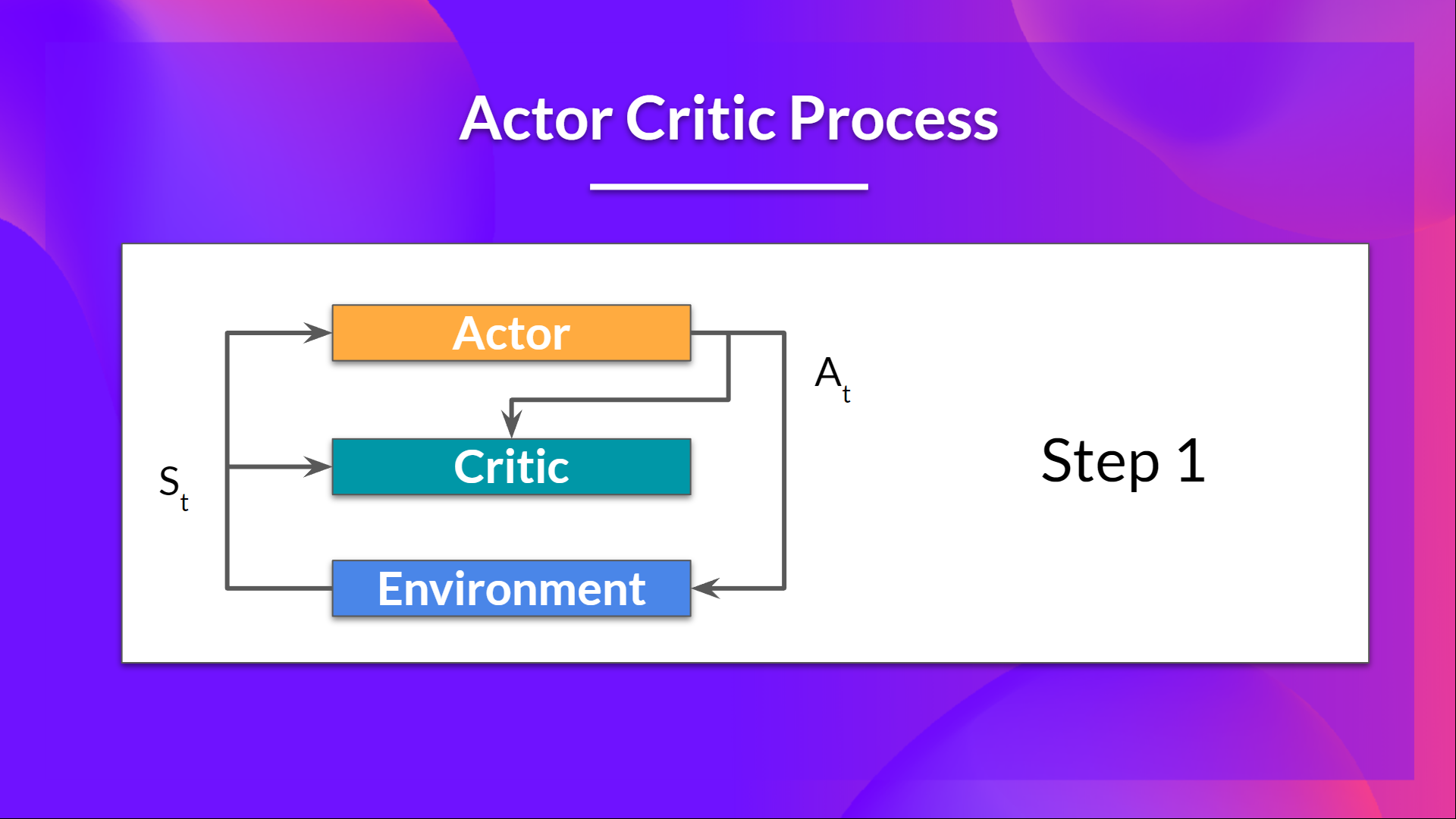
2.批评家还将该动作作为输入，并使用S_t 和 A_t 计算在该状态下采取该动作的价值：Q值。

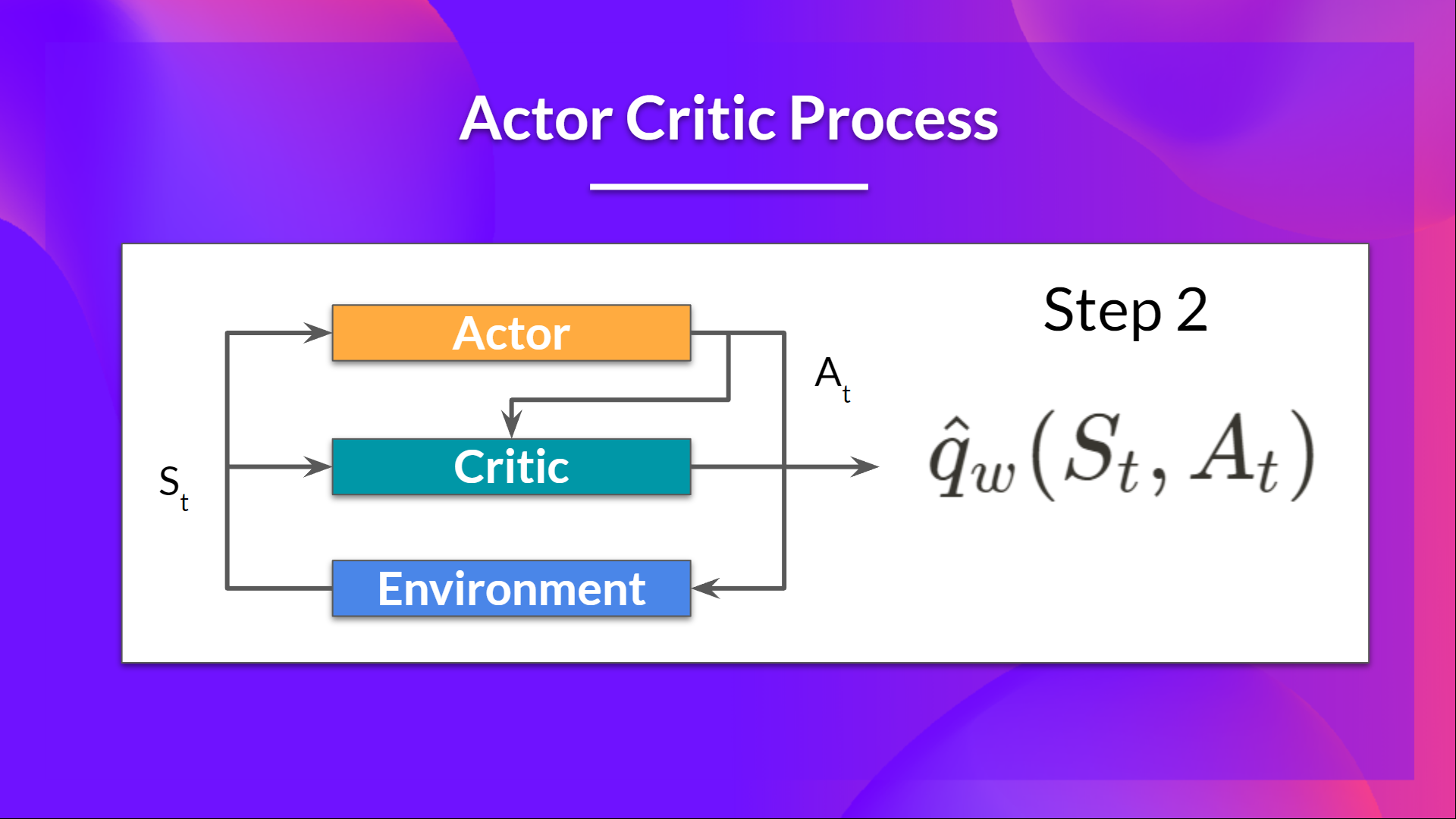
3.在环境中执行的动作 A_t 会产生一个新的状态 S_{t+1} 和奖励 R_{t+1}。

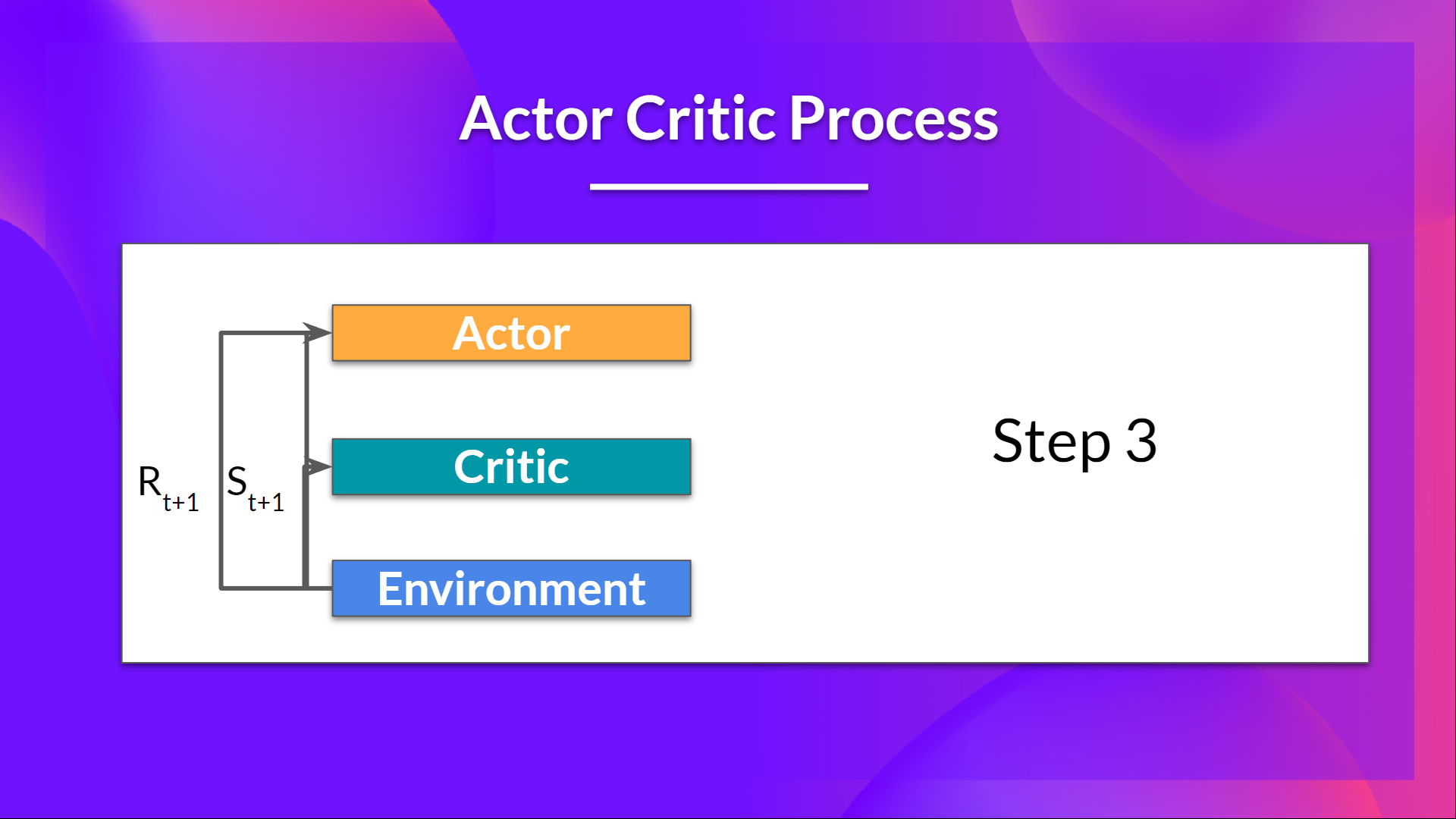
4.演员使用 Q 值来更新其策略参数。

5.由于其更新后的参数，演员会在给定新状态 S_{t+1} 的情况下产生下一步行动 A_{t+1}。然后评论家更新其价值参数。

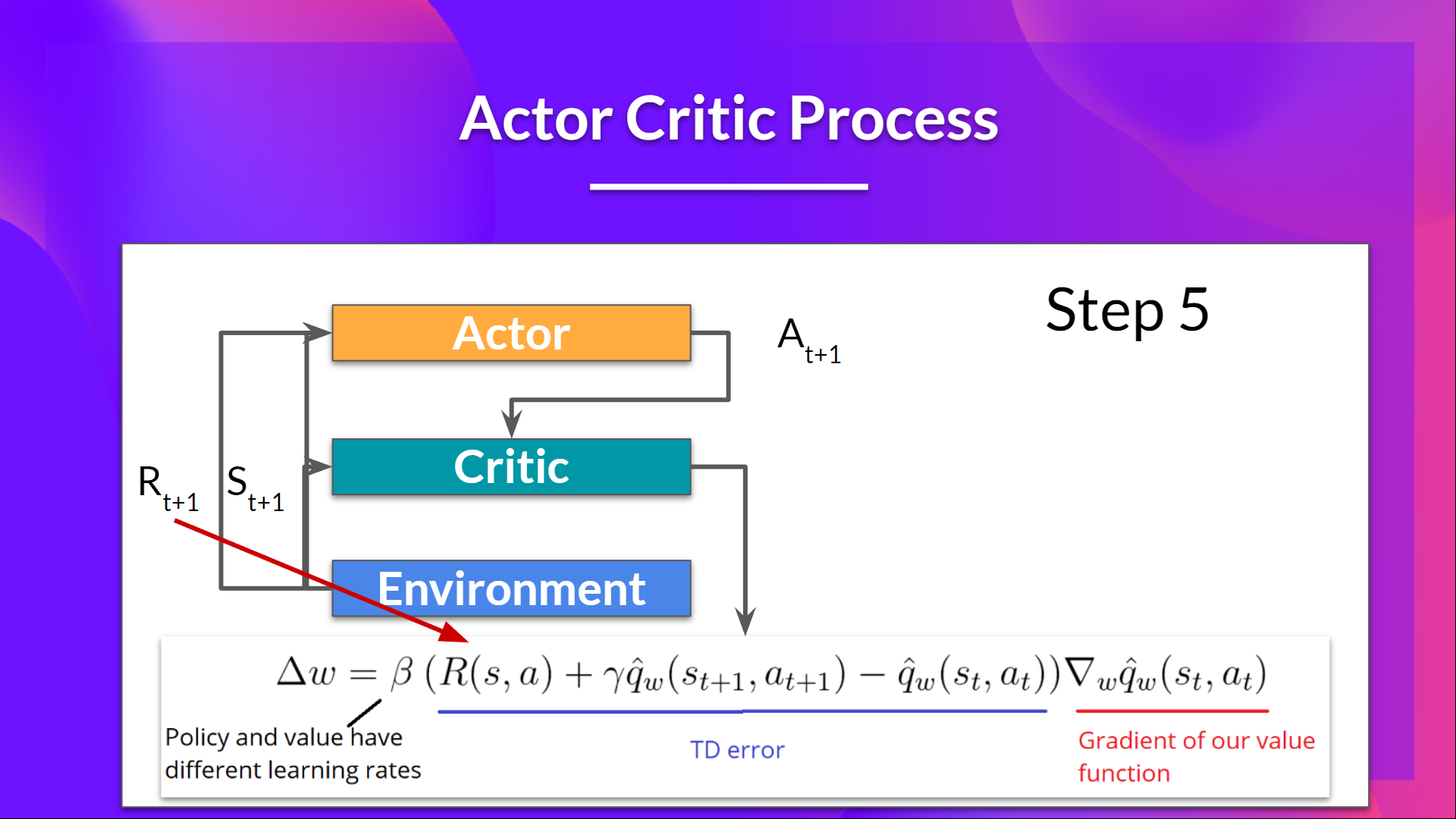
演员 (Actor) 在状态 s做出一个动作 a 。
环境给出奖励 r 和下一个状态 s'。
评论家 (Critic) 登场。它不看“一整局”的奖励，它只看“这一步”：
- 它会计算一个叫做 TD 误差 (TD-Error) 的东西： $\delta = r + \gamma V(s') - V(s)$ 。
- 翻译成人话：
  - $r + \gamma V(s')$ 是“我实际得到的奖励 + 下一个状态的预估价值”，这是我们认为的“更靠谱的价值”。
  - $V(s)$ 是“我之前对当前状态的预估价值”。
  - $\delta$ 就是“理想与现实的差距”。
$\delta$ (TD 误差) 的妙用：
- 指导演员： 如果 $\delta > 0$ （惊喜！你做的比预期的要好），演员就调整策略，增加这个动作 $a$ 的概率。如果 $\delta < 0$ （失望！你做的比预期的要差），演员就调整策略，减少这个动作 a 的概率。
- 指导评论家：评论家自己也要学习。它发现自己的 V(s) 估算得不准（导致了 $\delta$ 的出现），于是它也更新自己，让 $V(s)$ 更接近 $r + \gamma V(s')$ 。

二，合作与制衡的机理

让我们把 Actor 和 Critic 想象成两个正在共同学习的神经网络。

演员 (Actor)：它的参数是 $\theta_a$ 。它是一个策略网络，输入状态 $s$ ，输出动作的概率 $\pi(a|s; \theta_a)$
评论家 (Critic)：它的参数是 $\theta_v$ 。它是一个价值网络，输入状态 $s$ ，输出该状态的价值 $V(s; \theta_v)$ （一个标量，表示这个状态有多好）。

整个学习过程的核心，就是两个损失函数 (Loss Function)。

1. 评论家 (Critic) 的自我修养：如何成为一个“好”裁判？

评论家的工作是准确地评估状态的价值 V(s)。

它如何知道自己的评估 V(s) 准不准呢？它使用在第一篇中提到的“理想与现实的差距”—— TD 误差 $\delta$ 来衡量。

现实 (TD 目标)：我们在 $s$ 状态，做了动作 $a$ ，拿到了奖励 $r$ ，进入了下一个状态 $s'$ 。那么，一个“更靠谱”的 $s$ 状态的价值，应该是 $r + \gamma V(s')$ 。
- $r$ 是我们真实拿到的即时奖励。
- $V(s')$ 是我们对下一个状态的价值估计 ( $\gamma$ 是折扣因子)。
理想 (当前估计)： $V(s)$ ，即评论家当前对 s状态的价值估计。

TD 误差 $\delta$ (Temporal-Difference Error) 就等于“现实”减去“理想”：

$\delta = (r + \gamma V(s')) - V(s)$

这个 $\delta$ 就是评论家犯的“错误”。

评论家的学习目标 (Loss_Critic):

评论家的目标就是最小化这个错误。最直接的方法就是使用均方误差 (MSE):

Loss_Critic = $\delta^2 = ((r + \gamma V(s')) - V(s))^2$

如何更新： 我们使用梯度下降来最小化这个 Loss。这个过程和 DQN (或 Q-Learning) 的更新几乎一模一样。
深刻之处： 评论家在学习时，它只关心一件事：让自己的 $V(s)$ 预测尽可能地接近 $r + \gamma V(s')$ 。它不需要知道演员的策略是什么，它只是在被动地、客观地评估“演员所经历的状态”。

2. 演员 (Actor) 的自我提升：如何成为一个“好”演员？

演员的工作是优化策略 $\pi(a|s)$ ，以便拿到更高的总奖励。

在“盲目试错”的 REINFORCE 算法中，演员的更新信号是 $\nabla \log \pi(a|s) \cdot G_t$ 。其中 $G_t$ 是“一整局的（加折扣的）总奖励”。我们已经知道， $G_t$ 是一个高方差、不稳定的信号。

在 Actor-Critic 中，我们用评论家给出的 $\delta$ 替换掉 $G_t$ 。

为什么是 $\delta$ ？这正是 AC 算法最深刻的地方。

演员的学习目标 (Loss_Actor):

演员的目标是最大化“策略梯度”，这个梯度现在变成了：

$\nabla J(\theta_a) \approx \log \pi(a|s; \theta_a) \cdot \delta$

$\log \pi(a|s)$ ：这是“策略的梯度方向”。它告诉我们，要增加或减少 $a$ 动作的概率。
$\delta$ (TD 误差)：这是“指导信号”。

让我们看看 $\delta$ 是如何指导演员的：

如果 $\delta > 0$ ：
- 含义： $r + \gamma V(s') > V(s)$ 。这意味着，实际发生的（奖励R + 下个状态的价值 V(s')）好于我们的预期（V(s)）。
- 指导： 这是一个“惊喜 (Positive Surprise)”！说明演员在 s 状态下做的动作 a$是个好动作。
- 更新： 演员会更新 $\theta_a$ ，增加 $\log \pi(a|s)$ ，也就是提高这个动作 $a$ 在未来被选中的概率。
如果 $\delta < 0$ ：
- 含义： $r + \gamma V(s') < V(s)$ 。这意味着，实际发生的差于我们的预期。
- 指导： 这是一个“失望 (Negative Surprise)”！说明动作 $a$ 是个坏动作。
- 更新： 演员会更新 $\theta_a$ ，减少 $\log \pi(a|s)$ ，也就是降低这个动作 $a$ 在未来被选中的概率。

因此，演员的损失函数 (Loss_Actor) （因为优化器是最小化 Loss，所以我们加个负号）是：

Loss_Actor = $- \log \pi(a|s; \theta_a) \cdot \delta$

重要提示： 在计算这个 Loss 时， $\delta$ 被视为一个常数。我们不希望演员的更新“反向传播”到评论家网络中去。演员只管“听从”评论家的 $\delta$ 指令，而评论家则在另一条线（Loss_Critic）上自我修行。

3. 深刻的联系： $\delta$ 到底是什么？

我们一直说 $\delta$ 是 TD 误差，是“惊喜”。但在现代强化学习中，它有另一个更深刻的名字：优势函数 (Advantage Function) 的估计。

优势函数 $A(s, a)$ 的定义是：

$A(s, a) = Q(s, a) - V(s)$

$V(s)$ ：在状态 $s$ 时，“平均”能拿到的价值（遵循当前策略）。
$Q(s, a)$ ：在状态 $s$ 时，指定要执行动作 $a$ ，然后“平均”能拿到的价值。
$A(s, a)$ ：“执行动作 $a$ ” 这件事，比“按平均水平玩”要好多少？

$A(s, a)$ 是指导演员学习的完美信号。如果 A > 0，就该多做；如果 A < 0，就该少做。

问题是，我们只有一个 V(s) 网络（评论家），我们没有 Q(s, a) 网络啊？

别急，我们来推导一下：

根据 Q 函数的定义， Q(s, a)约等于 $E[r + \gamma V(s')]$ （在 $(s,a)$ 之后，期望的即时奖励+下一状态的价值）。

所以：

$A(s, a) = Q(s, a) - V(s) \approx (r + \gamma V(s')) - V(s)$

看！ $A(s, a) \approx \delta$

结论： 评论家在计算自己的 TD 误差 $\delta$ 时，在不经意间，计算出了“优势函数 A(s, a)” 的一个（有噪声的）单步估计值！

这就是 Actor-Critic 算法设计的精妙之处。评论家为了最小化自己的 $\delta^2$ 而努力学习 $V(s)$ ，而它在学习过程中产生的“副产品” $\delta$ ，恰好是演员所需要的、最好的指导信号 $A(s, a)$ 。

总结：完整的算法流程

现在我们把 Actor 和 Critic 组合起来，这个算法就是 Advantage Actor-Critic (A2C) 的基础版：

初始化： 演员网络 $\pi(a|s; \theta_a)$ 和评论家网络 $V(s; \theta_v)$ 。
循环（每一步）：

a. 演员表演：在当前状态 $s$ ， $a \sim \pi(a|s; \theta_a)$ 。

b. 环境反馈：得到 $r$ 和 $s'$ 。

c. 评论家评估：

i. 用评论家网络计算： $V(s) = V(s; \theta_v)$ 和 $V(s') = V(s'; \theta_v)$ 。

ii. 计算 $\delta$ (优势)： $\delta = r + \gamma V(s') - V(s)$ 。

d. 评论家学习：计算 Loss_Critic = $\delta^2$ 。对 $\theta_v$ 执行一步梯度下降。

e. 演员学习：计算 Loss_Actor = $- \log \pi(a|s) \cdot \delta$ 。对 $\theta_a$ 执行一步梯度下降（ $\delta$ 视为常数）。

f. 更新状态： $s \leftarrow s'$ 。

伪代码：

初始化 Actor 网络 π_θ 和 Critic 网络 V_w

循环：
    观察状态 s
    根据 Actor 生成动作 a
    执行动作，获得奖励 r 和新状态 s'

    # Critic 更新（学习评价）
    目标值 = r + γ * V_w(s')
    TD误差 δ = 目标值 - V_w(s)
    w ← w + 学习率 * δ * ∇V_w(s)

    # Actor 更新（学怎么做）
    θ ← θ + 学习率 * δ * ∇log π_θ(a | s)

    s ← s'

通过引入评论家 (Critic)，我们彻底解决“演员” (Policy-Based) 的高方差问题。

演员 (Actor) 不再需要等到一局游戏结束。
它每做一步，评论家 (Critic) 都会告诉它一个“即时反馈” ( $\delta$ )。
这个反馈信号 $\delta$ 远比一整局的总奖励 $G_t$ 要稳定、低方差。

这使得 Actor-Critic 既保留了 Policy-Based 方法处理连续动作和随机策略的能力，又获得了 Value-Based 方法的稳定性和单步更新的效率。

三. A2C 与 A3C 的演进（进阶）

我们已经深入了 AC 的核心机理。但这个“基础版AC”仍然存在问题（比如 $\delta$ 还是有噪声、训练不稳定等）。

为什么？因为它“近视”且“短视”。

“近视” (高方差的 $\delta$ )： 我们的 $\delta = r + \gamma V(s') - V(s)$ 严重依赖于 $V(s')$ 这个一步之后的估计。但 $V(s')$ 是由一个正在学习中的、不完美的评论家网络给出的，它自身的“噪声”很大，导致 $\delta$ 信号也忽高忽低，演员的策略更新还是不稳定。
“短视” (数据相关性)： 算法每走一步就更新一次。这意味着连续的更新步骤是高度相关的（ $s_{t+1}$ 总是接着 $s_t$ ），这使得训练过程非常低效且容易陷入局部最优（就像DQN需要经验回放池来打破这种相关性）。

为了解决这两个致命问题，Actor-Critic 进化成了它最著名的现代形态：A2C 和 A3C。

1. 解决“近视”问题：N-Step Returns (N步回报)

基础版 AC 用 $\delta = (r + \gamma V(s')) - V(s)$ 来指导演员。这里 $r + \gamma V(s')$ 被称为 TD 目标 (TD-Target)。

这个“目标”太“近”了，只看一步奖励 $r$ 。我们为什么不看得更远一点呢？

N-Step Returns (N步回报) 的思想：

我们不只看 1 步，我们让演员先表演 N 步（比如 N=5），收集这 N 步的真实奖励，然后再用 N 步之后的 $V$ 值来做估计。

1 步回报 (基础版AC)： $G_t^{(1)} = r_t + \gamma V(s_{t+1})$
2 步回报： $G_t^{(2)} = r_t + \gamma r_{t+1} + \gamma^2 V(s_{t+2})$
N 步回报： $G_t^{(N)} = r_t + \gamma r_{t+1} + ... + \gamma^{N-1} r_{t+N-1} + \gamma^N V(s_{t+N})$

现在，我们用这个“更可靠的 N 步回报” $G_t^{(N)}$ 来当做“现实” (TD 目标)。

于是，我们的“优势函数” (即 $\delta$ ) 变成了：

$A_t = \delta_t = G_t^{(N)} - V(s_t)$

这完美地在“偏差 (Bias)”和“方差 (Variance)”之间做了权衡。

REINFORCE (纯PG)： $G_t$ 是“一整局”的回报。它的“方差”极大（运气成分重），但“偏差”为0（完全基于真实奖励）。
基础版 AC： $G_t^{(1)}$ 是“一步回报”。它的“方差”很小（只依赖一步 $r$ ），但“偏差”很大（严重依赖不准的 $V$ 值）。
N 步 AC： $G_t^{(N)}$ 处在两者之间。它用了 N 步的“真实奖励”（低偏差），只在最后一步用了 $V$ 值的“估计”（低方差）。它是一个好得多的“指导信号”。

所有使用 N 步回报来计算优势 $A_t = G_t^{(N)} - V(s_t)$ 的 Actor-Critic 算法

统称为 Advantage Actor-Critic (A2C)。

2. 解决“短视”问题：Asynchronous (异步)

我们解决了“近视” (N-Step) 问题，但“短视” (数据相关性) 问题还在。我们仍然是在一条轨迹上“走 N 步，更新一次，再走 N 步...”。

DQN 使用“经验回放池 (Replay Buffer)”来打破相关性。Actor-Critic 能不能也用？

可以，但是很麻烦。因为 AC 是 On-Policy (在线策略) 算法，它学习的 $\pi(a|s)$ 和采集数据的 $\pi(a|s)$ 必须是同一个，Replay Buffer 里的“旧数据”不能随便拿来用（除非使用 Off-Policy 修正，如 PPO）。

DeepMind 在 2016 年提出了完全不同的解决方案，这就是 A3C (Asynchronous Advantage Actor-Critic)。

A3C 的核心思想：用“异步”来代替“经验回放池”。

它不是一个“Agent”在学习，而是一群“工人 (Worker)” 在学习。

Global Network (全局网络)： 我们有一个“主网络” (参数 $\theta_a$ 和 $\theta_v$ )。
N 个 Workers (N个工人)： 我们在 N 个 CPU 核心上（比如 16 个）分别创建 N 个“工人”。
并行探索： 每个“工人”都有自己独立的环境（比如一个独立的雅达利游戏模拟器）。
工作流程：
1. 每个“工人” $i$ 先从“主网络”复制一份最新的参数 $\theta_a$ 和 $\theta_v$ 到自己本地。
2. “工人” $i$ 在它自己的环境里，用本地的网络独立玩 N 步（比如 N=5）。
3. “工人” $i$ 用这 N 步的经验，计算出 $A_t$ (优势) 和 $V_t$ (价值目标)。
4. “工人” $i$ 计算出本地网络对“主网络”参数的梯度（ $\nabla \theta_a$ 和 $\nabla \theta_v$ ）。
5. “工人” $i$ 只把“梯度” 异步地（即算完就传，不管其他工人）发送回“主网络”。
6. “主网络”收到梯度后，更新自己的参数 $\theta_a$ 和 $\theta_v$ 。
7. “工人” $i$ 传完梯度后，立刻从“主网络”拉取最新的参数，然后回到第 2 步。

A3C 利用“空间”换“时间”。

它通过在同一时间、不同空间（不同环境）中收集大量不相关的经验，完美地解决了“数据相关性”问题。

“工人1”可能在游戏A的第10关；“工人2”可能刚在游戏B的第1关开始；“工人3”可能在游戏A的第5关即将失败...
当这些“五花八门”的经验所产生的梯度“混合”在一起时，更新信号就变得极其稳定和“去相关” (De-correlated)。
这使得 A3C 根本不需要 Replay Buffer，也不需要 GPU，它在 CPU 上就能表现得极其高效和强大。

3. 演进的终点：A2C (现代版)

A3C 的思想是革命性的，但“异步”更新在实现上很复杂（需要多线程锁、参数服务器）。

后来，研究者们（特别是 OpenAI）发现：我们真的需要“异步”吗？

A3C 的核心是“多个并行环境”带来的去相关性，而不是“异步”本身。

于是，一个更简单、更强大的版本出现了，它就是现代版的 A2C（有时也被称为“A2C (batched)”）：

同步 A2C (现代版)：
1. 我们依然有 N 个“工人”在 N 个并行环境里。
2. 同步开始： 所有工人同时开始，用相同的策略 $\pi$ 玩 N 步。
3. 同步等待： 等所有工人都完成了 N 步，把他们收集到的数据 (s, a, r, s') 全都汇总起来，形成一个大的 Batch (批次)。
4. 同步更新： 我们用这个大 Batch 的数据，计算一次总的 Loss (Actor 和 Critic)，并一次性地执行梯度下降。
5. 同步重复： 所有工人用更新后的新策略，回到第 2 步。