单调栈总结

最新推荐文章于 2025-10-25 08:58:04 发布

原创最新推荐文章于 2025-10-25 08:58:04 发布 · 1.6k 阅读

27 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构

声明：文章同步发布于我的洛谷博客。

顾名思义，单调栈就是栈内元素有序的栈。

说实话，我挺佩服发明单调栈的这个人的，竟然能想到这么做。

单调栈按照其数据存放的顺序分为单调递增栈和单调递减栈。

我们手动模拟一个单调递减栈：

初始时栈为空，总共添加 $4$ 个元素，分别为 $\{4,6,5,7\}$ 。

现在来了一个元素 $4$ ，栈变为： $[4]$ 。

添加一个元素 $6$ ， $4<6$ ，所以栈变为 $[4,6]$ 。

添加一个元素 $5$ ， $5<6$ ，栈变为 $[4,5]$ 。

添加一个元素 $7$ ， $7>5$ ，栈变为 $[4,5,7]$ 。

模拟结束。

相信到了这里大家应该对单调栈有了初步的了解，但是它具体有什么用呢？

1. 下一个更大（小）元素问题

比如我们在 P1901 发射站中，需要求解两边比它大的离它最近的元素，可以用单调栈解决。

2. 计算柱状图中的最大矩形面积

记得好像是 UVA 中的题目，题目的大致意思是：给定 $n$ 根相邻的柱子，每个柱子的宽度为 $1$ ，求能够勾勒出的最大矩形的面积。

维护出以 $a_i$ 为柱子高度（ $a$ 记录的是每个柱子的高度）能延伸的最大长度，将所有情况取最大值即可。

示意图：

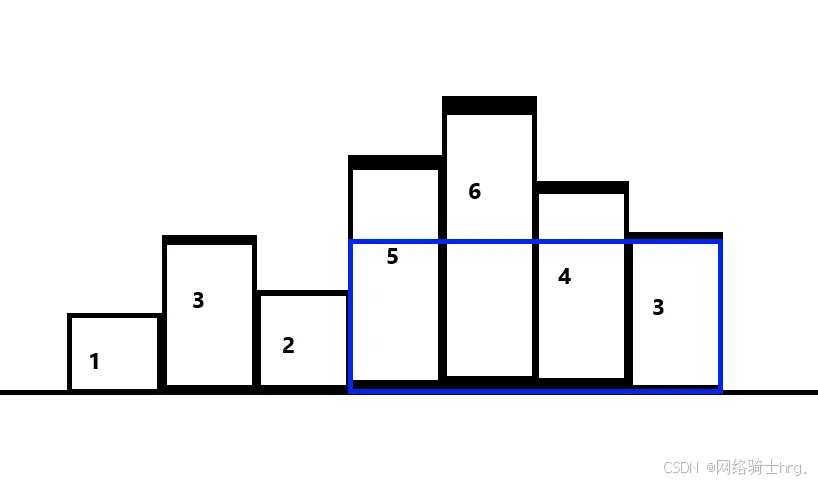
最大面积为： $3\times 4=12$ 。

例题1：P5788 【模板】单调栈

对于这道题，我们就以一个初学者的角度来讲一下这道题。

比如说有一串序列：

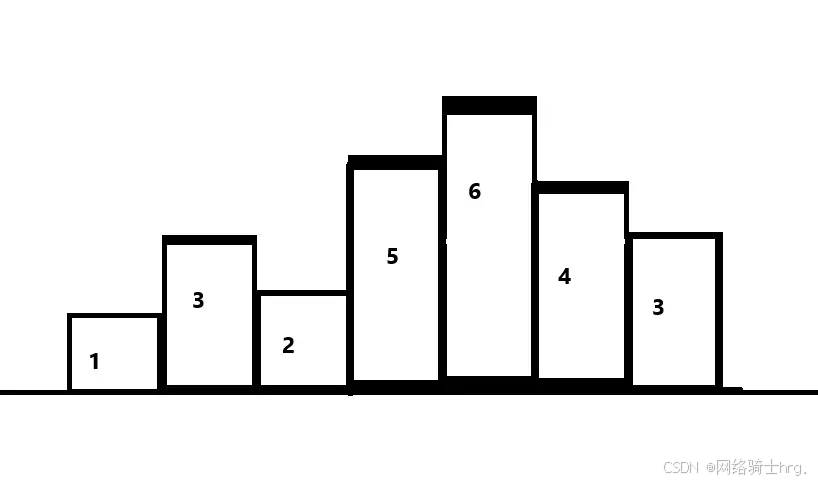
我们将题目简化为：有 $n$ 个数字，对于第 $i$ 个数字，求右边第一个大于它的数字的下标。

由于是求出右边第一个比它大的元素，我们维护一个单调栈。但是是单调递增栈还是单调递减栈呢？

我维护的是一个单调递减栈，如果当前栈顶比 $a_i$ 要小的话，说明栈顶右边的第一个大于它的元素是 $i$ ，存储答案。

实现

#include<bits/stdc++.h>
using namespace std;
int n,a[3000005],ans[3000005];
stack<pair<int,int>>st;
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=1;i<=n;i++){
        while(st.size()&&st.top().first<a[i]){
            ans[st.top().second]=i;
            st.pop();
        }
        st.push({a[i],i});
    }
    for(int i=1;i<=n;i++){
        cout<<ans[i]<<' ';
    }
    return 0;
}

例题2：P1901 发射站

跟例题1其实差不多，只不过是需要求出两边比它大的第一个元素。

我们做两边单调栈，一遍从 $1$ 到 $n$ ，维护一个单调递减栈，如果栈顶元素小于 $H_i$ ，那么就一直弹出栈顶，最后剩下的必然就是左边第一个比 $i$ 大的元素。

右边同理，只不过循环要从 $n$ 到 $1$ 。

最后统计一下答案即可。

实现

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,sum[1000005],ans,l[1000005],r[1000005];
pair<int,int>a[1000005];
stack<pair<int,int>>stl,str;
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i].first>>a[i].second;
    }
    for(int i=1;i<=n;i++){
        while(stl.size()&&stl.top().first<a[i].first){
            stl.pop();
        }
        l[i]=(stl.size()?stl.top().second:l[i]);
        stl.push({a[i].first,i});
    }
    for(int i=n;i;i--){
        while(str.size()&&str.top().first<a[i].first){
            str.pop();
        }
        r[i]=(str.size()?str.top().second:r[i]);
        str.push({a[i].first,i});
    }
    for(int i=1;i<=n;i++){
        sum[l[i]]+=a[i].second;
        sum[r[i]]+=a[i].second;
    }
    for(int i=1;i<=n;i++){
        ans=max(ans,sum[i]);
    }
    cout<<ans;
    return 0;
}

例题3：B3666 求数列所有后缀最大值的位置

首先得知道，异或的一个性质：

设一个数字 $x$ ，则 $x\oplus a\oplus a =x$ 。

由此可见，异或对答案造成的影响是可逆的。

那么，如果当前数字 $i$ 为后缀最大值，我们让 $ans \oplus i$ ，如果 $i$ 已经不是后缀最大值了，我们再让 $ans \oplus i$ ，抵消掉 $i$ 对 $ans$ 的影响（ $ans$ 记录的是答案）。

剩下的就是维护一个严格单调递减的单调栈。

注意：一定要写快读快写/关闭同步流/用 C 语言输入输出，否则会 TLE。而且要开 unsigned long long！！！

实现

#include<bits/stdc++.h>
using namespace std;
#define int unsigned long long
int n,ans,top;
pair<int,int>st[1000005];
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=1,x;i<=n;i++){
        cin>>x;
        while(top>0&&st[top].first<=x){
            ans^=st[top].second;
            top--;
        }
        ans^=i;
        cout<<ans<<'\n';
        st[++top]={x,i};
    }
    return 0;
}