哈希(Hash)函数是将输入(字符串)映射到输出(哈希值)的函数。
注意:函数名称不要用 hash,C++11 标准库中提供了这个函数。
想偷懒也可以用 unordered_map(底层为 Hash),不过容易被卡。
字符串哈希值分为三种情况:
- 单射:每个字符串都拥有唯一的哈希值(不全部用完)。
- 满射:每个字符串都有哈希值且哈希值全部用完。
- 双射:每个字符串都拥有唯一的哈希值且哈希值全部用完。
双射是最理想的情况,但是几乎不可能出现。
日常生活中通常出现的是单射或满射。
一般的计算公式为:
H a s h ( s ) = ∑ i = 0 n − 1 s i × p n − i − 1 m o d m Hash(s)=\sum_{i=0}^{n-1} s_i\times p_{n-i-1} \bmod m Hash(s)=i=0∑n−1si×pn−i−1modm
p 通常为一个冷门的偏小的质数(如: 131 , 1151 , 13331 131,1151,13331 131,1151,13331), m m m 一般为一个大质数(不要用 998244353 , 1 0 9 + 7 998244353,10^9+7 998244353,109+7 之类的常见的模数,容易被卡)。
哈希冲突
若两个字符串不同但是哈希函数值相同,则称之为哈希冲突。
最直观的体现就是代码 Wrong Answer。
如何解决?
1:自然溢出
我们都知道,unsigned 类型(无符号整型)仅能存储无符号整型。
我们可以理解为,若数字超出了 2 64 − 1 2^{64}-1 264−1 的最大限制,将自动对 2 64 2^{64} 264 取模。
注意加粗的那一部分,虽然 2 64 2^{64} 264(为 18446744073709551616 18446744073709551616 18446744073709551616)不是质数,但是因为过于巨大,所以哈希冲突的概率较小。
2:多重哈希
一般上双哈希就够了,不过也有三个甚至以上的,就统称为多重哈希好了。
单哈希即使用自然溢出,也可能会哈希冲突,所以多重哈希相当于又上了一道保险。
一个哈希函数中,两个字符串函数值相同并不代表这两个字符串一定相同,只有用多个哈希函数进行验证,才能降低哈希冲突的概率。
所以多重哈希的判断条件是:无论使用哪个哈希函数判断,得到的哈希值都是相等的。
双哈希例题:P3370 【模板】字符串哈希
单哈希过不了。
因此使用自然溢出+多重哈希。
对于两个哈希函数值,如果两个哈希函数值均不相同,则这时候可以判断这两个字符串不相同。
实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,ans=1;
pair<unsigned long long,unsigned long long>a[10005];
string s[10005];
unsigned long long Hash1(string s){
unsigned long long base=1129,sum=0;
for(auto z:s){
sum=sum*base+z;
}
return sum;
}
unsigned long long Hash2(string s){
unsigned long long base=2287,sum=0;
for(auto z:s){
sum=sum*base+z;
}
return sum;
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>s[i];
a[i]={Hash1(s[i]),Hash2(s[i])};
}
sort(a+1,a+n+1);
for(int i=2;i<=n;i++){
if(a[i]!=a[i-1]){
ans++;
}
}
cout<<ans;
return 0;
}
子串哈希
现在我们需要求字符串的某个区间的哈希值。
最直接的方法就是每次询问重新跑,但是时间不允许我们这样做。
把每个阶段的哈希值存储起来(类似于前缀和)。
假设字符串 s = abcd s=\texttt{abcd} s=abcd,则:
h s 0 = 0 h s 1 = ( h s 0 × p ) + a h s 2 = ( h s 1 × p ) + b h s 3 = ( h s 2 × p ) + c h s 4 = ( h s 3 × p ) + d hs_0=0\\ hs_1=(hs_0\times p)+\texttt{a}\\ hs_2=(hs_1\times p)+\texttt{b}\\ hs_3=(hs_2\times p)+\texttt{c}\\ hs_4=(hs_3\times p)+\texttt{d}\\ hs0=0hs1=(hs0×p)+ahs2=(hs1×p)+bhs3=(hs2×p)+chs4=(hs3×p)+d
假设我们截取的字符串叫 bc \texttt{bc} bc。
类似于前缀和,此时的哈希值为:
h s r − h s l − 1 × p r − l + 1 hs_r-hs_{l-1}\times p^{r-l+1} hsr−hsl−1×pr−l+1
子串哈希例题:P10468 兔子与兔子
因为暴力枚举无法通过本题,所以需要使用字符串哈希。
首先记录下第 i i i 位字符的哈希值,以及 p i p^i pi 的值。
对于每次询问,求出两个区间的哈希值,判断哈希值是否相等即可。
实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,ans=1,m;
unsigned long long base=2341,mod=10000139,hs[1000005],pw[1000005];
string s;
unsigned long long get_Hash(int l,int r){
return hs[r]-hs[l-1]*pw[r-l+1];
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>s;
s=' '+s;
pw[0]=1;
for(int i=1;i<s.size();i++){
hs[i]=hs[i-1]*base+s[i];
pw[i]=pw[i-1]*base;
}
for(cin>>m;m;m--){
int l1,r1,l2,r2;
cin>>l1>>r1>>l2>>r2;
cout<<(get_Hash(l1,r1)==get_Hash(l2,r2)?"Yes":"No")<<'\n';
}
return 0;
}
回文哈希
回文哈希可以替代一部分 Manacher 的功能。
回文哈希的作用就截取一个子串,判断这个子串是否为回文串。
若正向得到的哈希值与反向得到的哈希值相等,则这个字符串是回文串。
将需要判断回文的字符串,一分为二。
以 M 形字符串 为例题。
判断是否为 M 串的条件:
- 本身为回文串。
- 左端点到中间端点分完之后的字串也是回文串。
实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,ans;
unsigned long long base=2777,hs[200005],hs2[200005],pw[200005];
string s,s1;
unsigned long long get_Hash1(int l,int r){
return hs[r]-hs[l-1]*pw[r-l+1];
}
unsigned long long get_Hash2(int l,int r){
return hs2[r]-hs2[l-1]*pw[r-l+1];
}
bool check(int l,int r){
return (get_Hash1(l,r)==get_Hash2(n-r+1,n-l+1));
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>s;
s1=s;
n=s.size();
reverse(s1.begin(),s1.end());
s=' '+s,s1=' '+s1;
pw[0]=1;
for(int i=1;i<=n;i++){
hs[i]=hs[i-1]*base+s[i];
hs2[i]=hs2[i-1]*base+s1[i];
pw[i]=pw[i-1]*base;
}
for(int i=1;i<=n;i++){
if(check(1,i)&&check(1,(i+1)/2)){
ans++;
}
}
cout<<ans;
return 0;
}
矩阵哈希(二维哈希)
我们将 n × m n\times m n×m 的哈希值排列为一个矩阵。
如何求子矩阵的哈希值?
以 P10474 [ICPC-Beijing 2011] Matrix 矩阵哈希 为例,需要求子矩阵的哈希值:
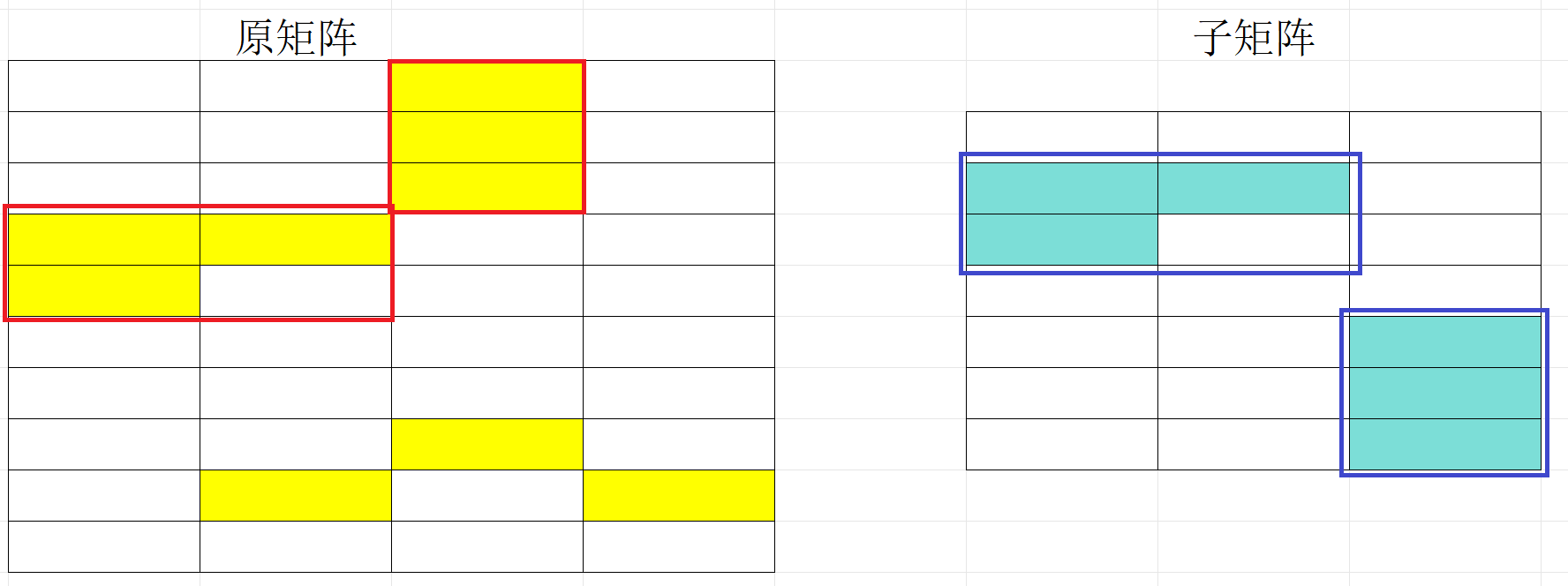
考虑以行为单位,直接进行一维的哈希处理。
暴力存储所有长度的哈希值。
设 h s l e n , x , y hs_{len,x,y} hslen,x,y 表示长度为 l e n len len,起点为 ( x , y ) (x,y) (x,y) 的矩阵哈希值。
当前矩阵+新的一行的哈希值为:
原来矩阵的哈希值 × p 行数 − 1 × 列数。 原来矩阵的哈希值\times p_{行数-1}\times 列数。 原来矩阵的哈希值×p行数−1×列数。
固定一个长度为 A × B A\times B A×B 的窗口 ( i , j ) (i,j) (i,j)。
移动到下一行:
新的矩阵哈希值 = = = 上个矩阵的哈希值 − - − 原来第 i i i 行的哈希值 × p A × B + \times p_{A\times B}~+~ ×pA×B + 最新一行的哈希值。
有点类似于滑动窗口。




















 1万+
1万+










