声明:该文章同步发表于我的洛谷博客。
从名字上来看,树状数组就是一个形状像树的数组。
二叉树和树状数组结构对比图:
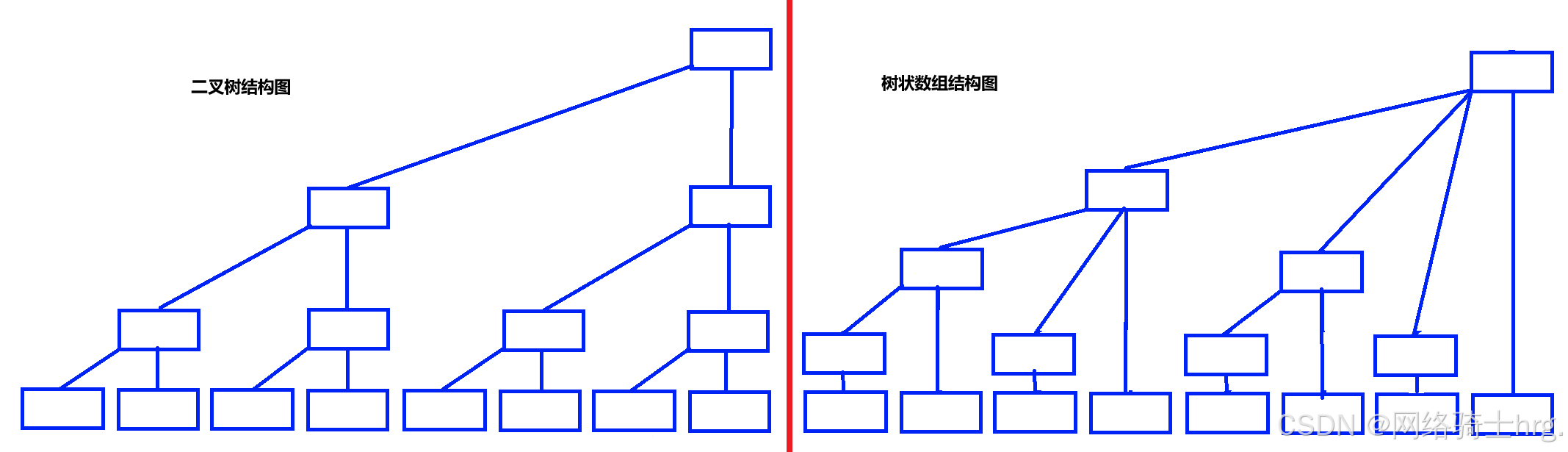
可以发现树状数组虽然和二叉树结构相近,但是删除了一部分。
为什么呢?
再给出另一张结构图:
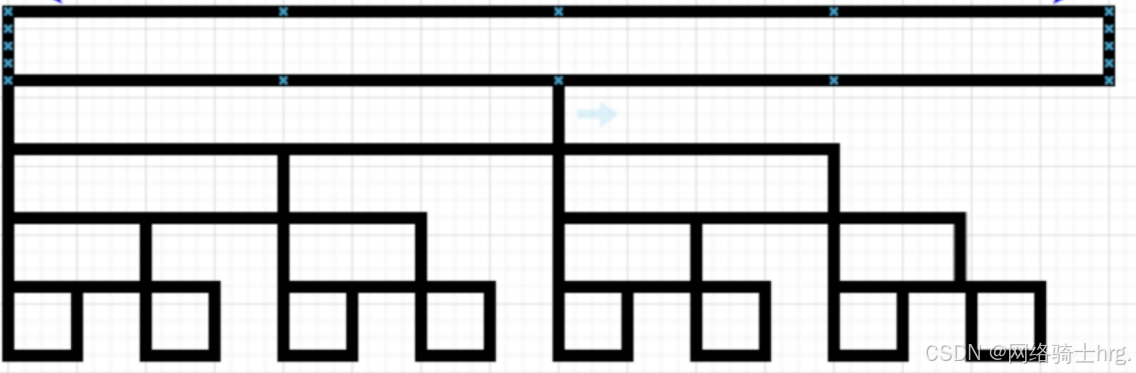
可以发现,每一层中的第偶数个格子是无用的,第奇数个格子是有用的,
这是因为,对于第 层第
个格子(
),一定可以用第
层第
个格子减去第
层第
个格子得到。
那么怎么求解呢?
我们用 维护一个树状数组。
初始化:
是不是挺麻烦的?
没错!我们可以用前缀和计算,记为 。
得出结论:(
)。
Q:函数 是干什么的?
A:对于 ,
的返回值为
的二进制抹掉最后一位
。
用 C++ 代码表示为:
int lowbit(int x){
return x&(-x);
}Q:ST 表的区间长度为 次方,那么树状数组的区间长度为多少呢?
A:根据上面的式子,可以得出 表示的区间长度为
。
单点修改,区间查询
说了这么多,还没讲树状数组怎么用。
如果我们修改了第 个点,那么只需要更新
以及它的父节点,即:
void modify(int x,int val){
while(x<=n){
c[x]+=val;
x+=lowbit(x);
}
}在查询时,我们将 和它的子节点的值加起来,实现为:
void modify(int x,int val){
while(x<=n){
c[x]+=val;
x+=lowbit(x);
}
}
那怎么区间查询呢?如果我们维护的是区间 元素之和,那么可以用类似于前缀和查询的操作,将区间
的结果减去区间
的结果。
区间修改,单点查询
对于这种情况,单点修改已经不能满足我们的要求(总不可能一个一个去加吧),既然是单点查询,那么我们可以考虑使用差分的思想。
假设我们要将区间 的每一个数加上
,那么我们将
加上
,
减去
,注意这种情况
不需要初始化,因为
维护的是差分的值。
查询时,输出 a[i]+query(i)。
区间修改,区间查询
好像大家都说这玩意用线段树才能做?
其实某些特殊的地方还是可以用的。
放道例题:P2184 贪婪大陆。
一张示意图:
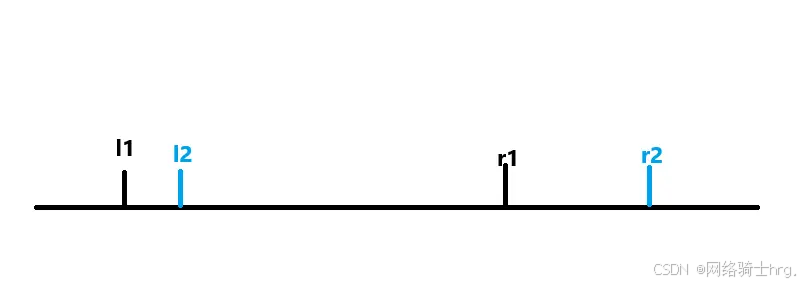
假设我们已经求出了区间 ,
的结果,现在我们添加一个区间
:
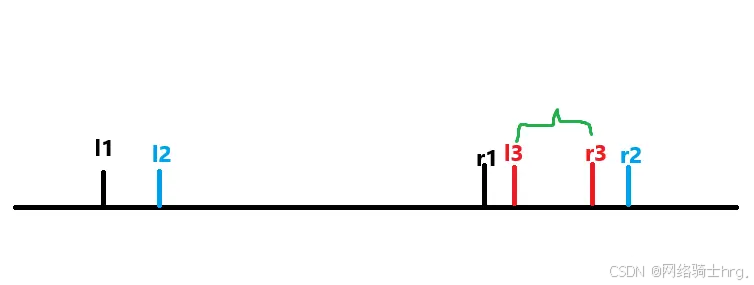
不难发现,区间 内树的种类等于
中左边界的数量减去区间
中右边界的数量。
所以我们就将这题转化为一道树状数组单点修改,区间查询的题目了。
注意:树状数组对于区间修改,区间查询问题仅能解决一部分特殊的问题。所以大家还是老老实实地去学习线段树吧。
离散化
本来不想写的,可以某些地方要用啊。
假设某道题,元素的最大数值达到了 ,但是元素数量只有
,这时候你会选择怎么办呢?
我们通常使用的方法为离散化。
方法1
首先将原数组复制一份。
然后将副本排序,将副本中的数据去重(否则可能会出现数字相同但是离散化后的值不同的情况)。
将原数组的每一个元素在副本中的位置作为离散化后的值。
方法2
使用数据结构(用 C++ 自带的 map/unordered_map)。
对于每一个数据,如果之前没出现过,那么给它分配一个编号并返回,否则返回之前分配的编号。
Q:是使用 map 更优还是用 unordered_map 更优呢?
A:根据情况而定。一般情况下 unordered_map 会比 map 要更快,但是不太稳定,容易被卡。建议在 OI 赛制中或打 Codeforces 时使用 map,因为在 OI 赛制中看不到实时反馈,Codeforces 比赛中用 unordered_map 基本会被其他选手 Hack 掉。如果在其他赛制中用 map 只超时了一点点,可以考虑用 unordered_map 卡常。




















 936
936

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








