0. 当主流 LLM中MoE 已成核心力量
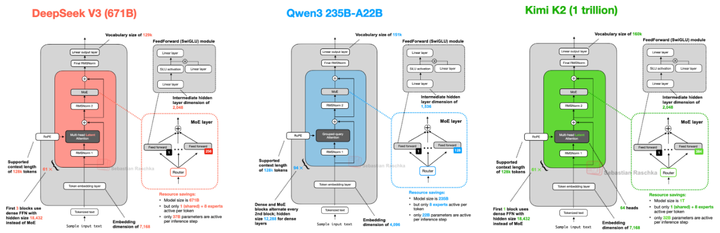
近几年,随着大型语言模型(LLM)朝着更高性能、更大规模扩展,Mixture‑of‑Experts(MoE)架构正从理论验证走向主流部署,成为构筑高效超大模型的重要支撑点(如下图)。
MoE
为什么说 MoE 是当前 LLM 架构革新的核心?
-
性能与效率并行。以 DeepSeek‑V3 为例,它采用 MoE 架构实现了 6710 亿参数的惊人规模,却通过每个 token 仅激活 256 个专家(加上一个共享专家),保持了极低的推理与训练成本arXiv。在实际评测中,其综合性能已接近闭源模型如 GPT‑4o 和 Claude 3.5,同时训练时间仅为传统模型的零头,也在性能/成本比上领先维基。
-
逐步成为多方看重的核心架构。无论是在技术社区还是产业链中,MoE 正逐步被多个团队视为突破模型扩展瓶颈的“秘密武器”。
-
主流模型中崛起的重要趋势。尽管像 GPT 和 LLaMA 系列最初使用的是密集 Transformer 架构,但随着硬件成本和性能压力增大,MoE 正被越来越多的开源与闭源团队积极探索。例如开源的 Mixtral 模型基于 Mistral-7B 构建 MoE 系统;Meta 的 LLaMA 4(代号“Scout” 或 “Maverick”)据传亦可能集成多模态专家结构;而 DeepSeek、DBRX 等新一代模型则将 MoE 作为核心设计,从开源到闭源都有接纳该路径的趋势。
1. MoE概念起源与基本原理
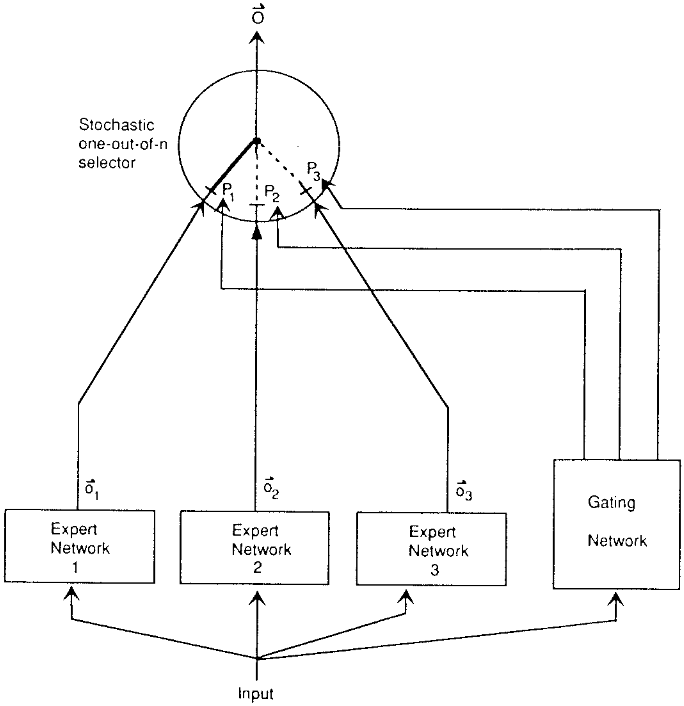
Mixture-of-Experts(MoE)的提出。 MoE是一种机遇性组合模型策略,其核心思想是使用多个“专家”模型共同完成学习任务,并由一个门控网络(gating network)根据输入特征选择适当的专家来产生输出giete。这一思想最早可追溯至1991年Jacobs等人提出的“局部专家自适应混合”模型Toronto。他们在论文中展示了一种监督学习方法:由多个独立的网络组成,每个专家网络负责训练数据的一个子集(针对特定子任务)。门控网络根据输入样本的特征决定启用哪一个专家或多个专家共同作用,从而将不同的输入子空间划分给最擅长该区域的专家处理。这种“分而治之”的结构可以减少不同子任务之间的相互干扰,使每个专家专注于其擅长的领域giete.ma。在Jacobs等人的原始设计中,门控网络输出一个softmax权重向量,对所有专家的输出进行加权求和作为最终预测,因此是一种软选择机制(soft routing),并未对专家实施硬性选择限制。这一模型在语音元音辨识等任务上验证了其可行性,通过将复杂任务划分为若干易于学习的子任务,每个子任务由特定专家解决,从而提升整体性能。
Original MoE
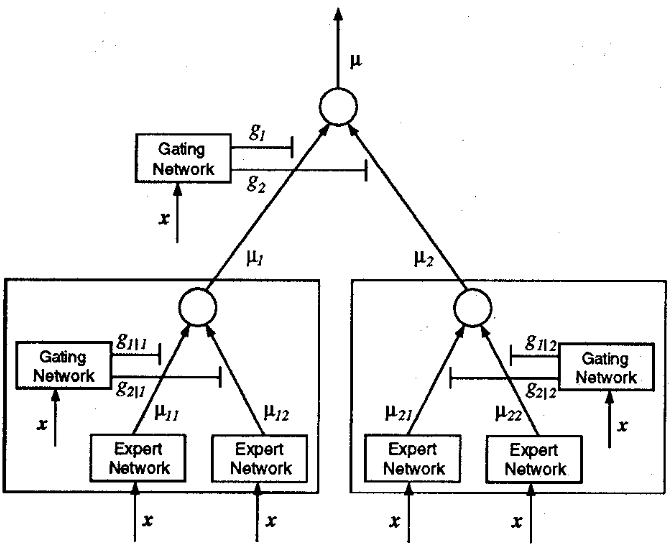
分层MoE与理论基础。 1993年,Jordan和Jacobs进一步扩展了MoE架构,引入了分层混合专家(Hierarchical MoE)的概念Toronto。在分层MoE中,多个专家可以按层次结构组成树状网络,顶层由一个门控网络根据输入先选择某个子树(子任务范围),再由该子树内部的次级门控网络选择具体的专家。这种层次化结构等价于在不同粒度上对输入进行路由,将原本单层门控扩展为多级决策,从而提高模型对复杂任务的表达能力。Jordan等人的工作表明,将门控网络置于树的根节点并允许各子节点拥有各自的门控和专家,可以实现更灵活的专家组合,有效地模拟更加复杂的决策过程。Jacobs和Jordan的两篇开创性论文奠定了MoE架构的基础:即通过门控机制动态选择模型的一部分(专家网络)来对输入做出响应,从而将整个网络划分为若干具有专长的子网络协同工作giete.ma。这一思想在上世纪90年代被提出时,曾被视作集合学习(Ensemble learning)的一种形式wiki,但由于当时计算资源和训练手段的限制,MoE并未得到大规模应用。总体而言,MoE的基本原理在于用一个轻量级的路由函数(门控网络)将输入映射到多个专家中的一个或少数几个,使不同专家各司其职、互不干扰地学习各自的数据子分布,然后将它们的输出按一定权重合并为最终结果。
Hierarchical MoE
2. 大型语言模型中MoE的作用与优势
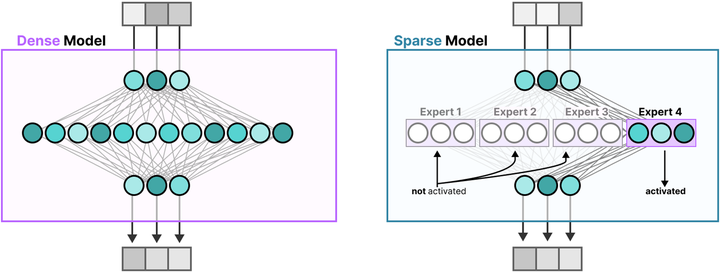
提升参数规模而计算成本可控。 在大型语言模型(LLM)的训练和推理中,MoE机制展现出了独特优势。传统的密集模型(dense model)对每个输入都激活模型中的全部参数,参数规模与计算开销呈线性相关。而MoE采用稀疏激活策略(稀疏模型,Sparse Model):每个输入仅激活模型中一小部分专家参数,由此使模型总参数量可以远大于实际每次计算所用的参数(参考下图)。
Dense model and Sparse Model
这一特性实现了模型容量与计算成本的解耦——增加专家数量可以大幅提高模型容量和潜在性能,但由于每次仅调用少数专家(如下图),推理和训练的计算开销增长有限arxiv。例如,有文献指出相比同等参数规模的稠密模型,MoE模型在训练和推理时所需的计算量显著降低,因为每个token只会激活少量专家,而非所有参数medium。
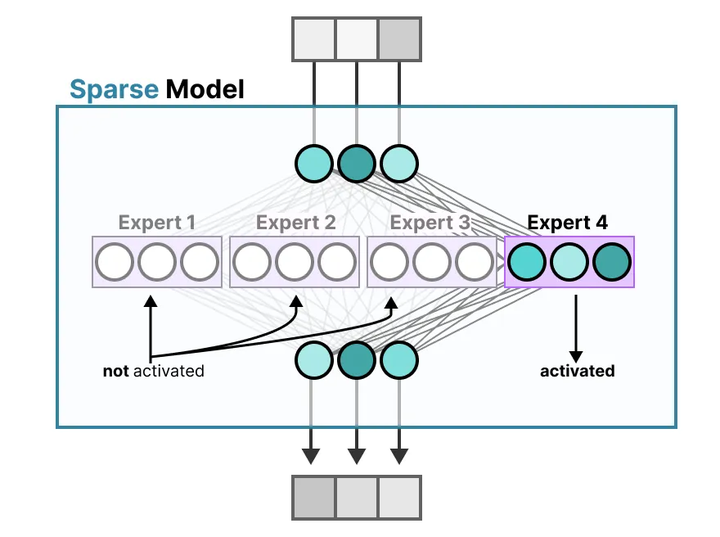
MoE
这种参数高效性使得MoE模型能够在保持计算预算接近恒定的情况下扩展至数十亿甚至万亿级参数,从而提升模型性能(如降低困惑度或提高下游任务精度)arxiv。简而言之,MoE允许在不等比例增加计算成本的情况下堆叠更多参数,突破了密集Transformer架构按算力缩放的瓶颈(例如,DeepSpeed-MoE的结果如下,arxiv)。
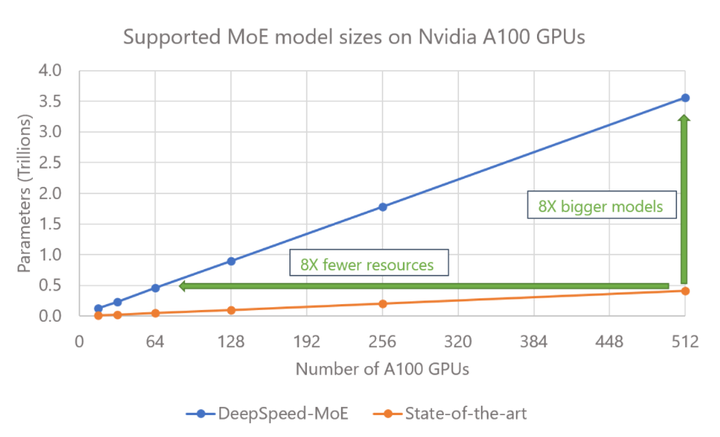
DeepSpeed-MoE
专家特化带来的性能提升。 除了计算效率,MoE通过专家网络的“特化”还能带来模型质量上的提升。由于每个专家只见到某类特定模式的输入,因而学习到更加精细的特征表示medium。大型语言模型往往需要处理多样化的语言现象和任务,





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 922
922

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








