蓝桥杯备考----＞二进制优化多重背包

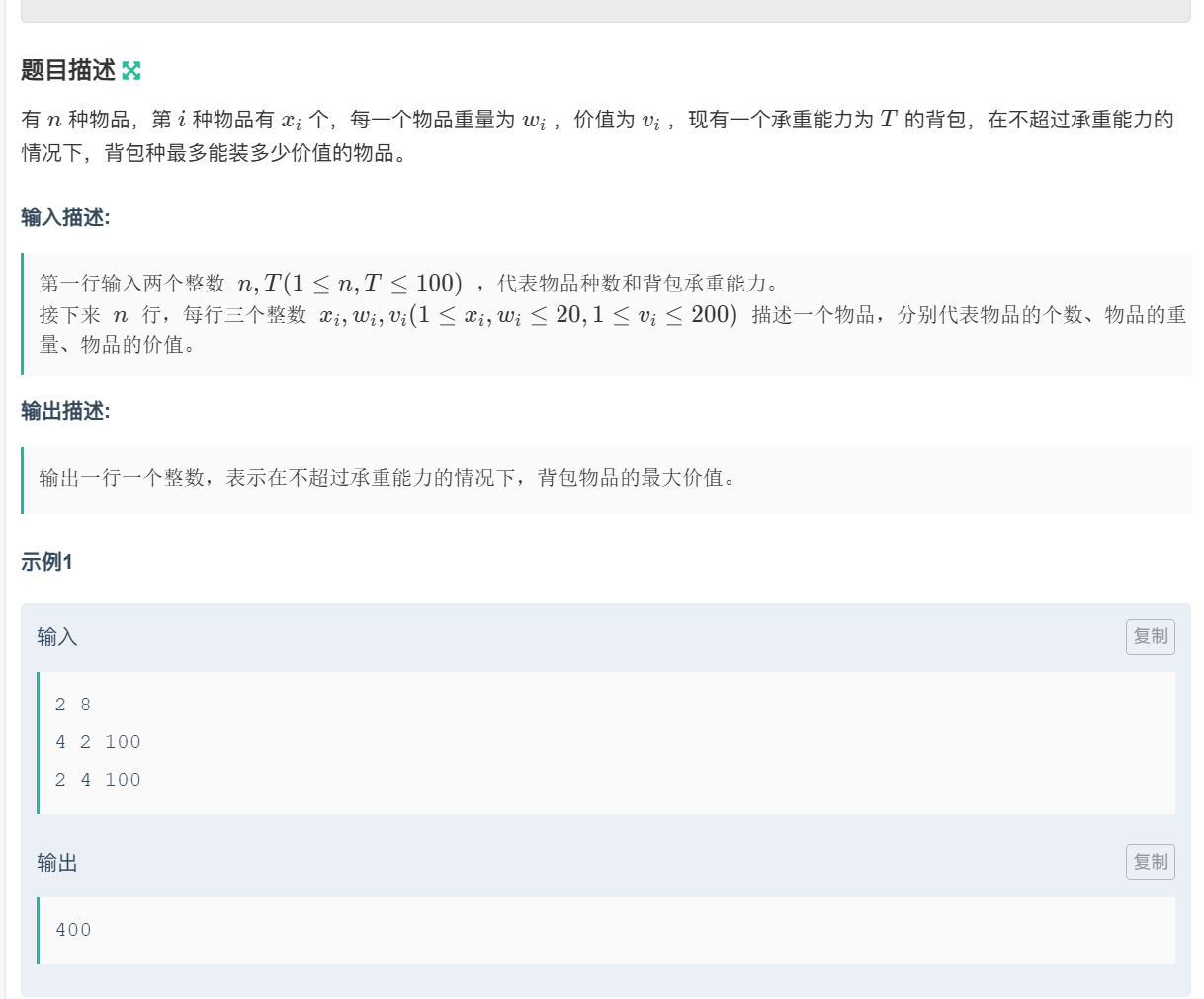
之前我们说过了普通版本的多重背包，接下来我们将会说说怎么优化

我们 普通版本的多重背包，时间复杂度是 O（n*m*x）

而我们优化后的多重背包，时间复杂度是 O（n*m*logx)

我们怎么优化呢，我们可以把每个多重背包拆成他的所有权重个堆儿

比如说某个物品我们有15个，我们可以把它拆成1个，2个，4个，8个，

然后用01背包的方法来解决多重背包，即可。

当然我们这种方式是不适用于求有多少策略的，因为如果要求多少策略的话，某个物品选2个和选2个 和某个物品选1个和选3个会记作两个策略，实际上他俩都是一个物品选了四次，其实就是一个策略，我们最终结果就偏大，当然，我们要是求个最大价值最小价值还是能求滴

本题，每个物品最多为20个，20可以拆成1+2+4+8+5,所以最多情况就是物品多出五倍来

#include <iostream>
using namespace std;
const int N = 110*5;
typedef long long ll;
int n,m;//n表示n个物品，m表示背包容量 
int v[N],w[N]; 
int pos;
ll f[N];


int main()
{
	cin >> n >> m;
	
	for(int i = 1;i<=n;i++)
	{
		int x,y,z;cin >> x >> y >> z;
		int t = 1;
		while(x>=t)
		{
			++pos;
			v[pos]=t*y;
			w[pos]= t*z;
			x-=t;
			t*=2;
		}
		if(x)
		{
			++pos;
			v[pos] = x*y;
			w[pos]=x*z;
		}
	}
	//接下来就按照01背包的做法来
	for(int i = 1;i<=pos;i++)
	{
		for(int j = m;j>=v[i];j--)
		{
			
				f[j] = max(f[j],f[j-v[i]]+w[i]); 
			
		}
	 } 
	cout << f[m]<< endl;
	
	
	
	
	
	return 0;
}