【蓝桥杯】Python 模版

1 字符串

1.1 字符串哈希

MOD = int(1e9+7)
p = 13331
n = len(s) # 文本串s,长度为n
h = [0] * (n + 5)
for i in range(1, n + 1):
    h[i] = h[i-1] * p + ord(s[i-1]) - ord('A')
    h[i] %= MOD
### 区间和
P = (p ** m) % MOD # 匹配串t的长度为m
(h[r] - h[l-1] * P % MOD + MOD) % MOD

1.2 KMP

n, m = len(s), len(t) # 文本串s和模式串t
ne = [0] * (n + m + 5)
ans, j = 0, 0
cur = t + '#' + s
for i in range(1, n + m + 1):
    while j > 0 and cur[i] != cur[j]:
        j = ne[j-1] # 回退
    if cur[i] == cur[j]:
        j += 1 
    ne[i] = j
    if ne[i] == m and i > m:
        ans += 1

1.3 字典树

# 以01字典树为例
tr = [[0, 0] for _ in range(5 * int(2e5+10))]
cnt = [0] * (5 * int(2e5+10))
ind = 0

def insert(x): # 插入节点
    global ind
    p = 0
    for i in range(20, -1, -1):
        j = x >> i & 1
        if not tr[p][j]:
            ind += 1
            tr[p][j] = ind
        p = tr[p][j]
    cnt[p] += 1 # 记录字符串x出现的次数

def find(x):  # 查找字符串
    p = 0
    for i in x:
        c = ord(i) - ord("a")
        if not tr[p][c]:
            return False
        p = tr[p][c]
    return cnt[p]        

def query_max(x): # 求异或极大值
    res, p = 0, 0
    for i in range(20, -1, -1):
        j = x >> i & 1
        if tr[p][not j]: # 异或运算性质
            res += 1 << i
            p = tr[p][not j]
        else:
            p = tr[p][j]
    return res

def query_min(x): # 求异或极小值
    res, p = 0, 0
    for i in range(20, -1, -1):
        j = x >> i & 1
        if tr[p][j]:
            p = tr[p][j]
        else:
            res += 1 << i
            p = tr[p][not j]
    return res

2 数学

2.1 快速幂

def qpow(a, b):
    res = 1
    while b:
        if b & 1:
            res = res * a % MOD
        a = a * a % MOD
        b >>= 1
    return res % MOD

2.2 数论分块

2.3 线性筛求欧拉函数和约数个数

phi[1] = 1
d[1] = 1
for i in range(2, n + 1):
    if not vis[i]:
        phi[i] = i - 1 # i的欧拉函数值
        d[i] = 2 # i的约数个数
        num[i] = 1 # i的最小质因子出现次数
        prime.append(i)
    for pri in prime:
        if pri * i > n:
            break
        vis[i * pri] = pri
        if i % pri == 0:
            phi[i * pri] = phi[i] * pri
            num[i * pri] = num[i] + 1
            d[i * pri] = d[i] // num[i * pri] * (num[i * pri] + 1)
            break
        phi[i * pri] = phi[i] * phi[pri]
        num[i * pri] = 1
        d[i * pri] = d[i] * 2

2.4 欧拉定理及其扩展

t/528c150d1c16482fad221aa75c9ae345.png)

2.5 线性求逆元

inv[1] = 1
for i in range(2, n + 1):
    inv[i] = (p - p // i) * inv[p % i] % p
# 下面是求阶乘逆元
inv[n+1] = qpow(fac[n+1], mod-2)
for i in range(n, -1, -1): 
    inv[i] = inv[i+1] * (i + 1) % mod

2.6 常见数列求和公式

等差数列

等比数列

平方数求和

立方数求和

递增数列求和（1+3+6+10+15……）

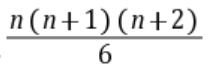
3 图论

3.1 树链剖分求LCA

def dfs1(x, fa):
    dep[x] = dep[fa] + 1
    siz[x] = 1
    f[x] = fa
    for y in G[x]:
        if y == fa:
            continue
        dfs1(y, x)
        siz[x] += siz[y]
        if not son[x] or siz[son[x]] < siz[y]:
            son[x] = y

def dfs2(x, t):
    top[x] = t
    if not son[x]:
        return 
    dfs2(son[x], t)
    for y in G[x]:
        if y == f[x] or y == son[x]:
            continue
        dfs2(y, y)

def LCA(x, y):
    while top[x] != top[y]:
        if dep[top[x]] < dep[top[y]]:
            x, y = y, x
        x = f[top[x]]
    return x if dep[x] < dep[y] else y

4 动态规划

4.1 背包（c++模板）

V:总重 w[]:各物品重量 c[]:各物品价值 

0/1背包 
for(int i=1;i<=n;i++) 
	for(int j=V;j>=w[i];j--) 
		f[j]=max(f[j],f[j-w[i]]+c[i]);

完全背包 
for(int i=1;i<=n;i++) 
	for(int j=w[i];j<=V;j++) 
		f[j]=max(f[j],f[j-w[i]]+c[i]);

p[]:各物品的数量
 
多重背包O(nmlogp)
for(int i=1;i<=n;i++)
{
	int num=min(p[i],V/w[i]);
	for(int k=1;num>0;k<<=1)
	{
		if(k>num) k=num;
		num-=k;
		for(int j=V;j>=k*w[i];j--)
			f[j]=max(f[j],f[j-k*w[i]]+k*c[i]);
	}		
}

T:总时间 t[]:各个物品的时间 

二维费用背包
for(int i=1;i<=n;i++) 
	for(int j=V;j>=w[i];j--) 
		for(int k=T;k>=t[i];k--) 
			f[j][k]=max(f[j][k],f[j-w[i]][k-t[i]]+1);

lim:总组数 num[]:各组里物品的数量 g[i][k]:第i组第k个物品的下标 
 
分组背包
for(int i=1;i<=lim;i++)
	for(int j=V;j>=0;j--)
		for(int k=1;k<=num[i];k++)
			if(j>=w[g[i][k]])
				f[j]=max(f[j],f[j-w[g[i][k]]]+c[g[i][k]]);

4.2 数位dp

def dfs(i, cnt, limit):
    if cnt > k: return 0
    if i == len(s): return int(cnt == k)
    if (i, cnt, limit) in hashmap:  # 记忆化处理
        return hashmap[(i, cnt, limit)]
    ans = 0
    up = int(s[i]) if limit else 1
    for d in range(up+1): 
       ans += dfs(i+1, cnt + int(d == 1), limit and up == d)
    hashmap[(i, cnt, limit)] = ans
    return ans
dfs(0, 0, True)

5 数据结构

5.1 树状数组

def lowbit(x):
    return x & (-x)

def modify(x, k):
    while x <= n:
        tr[x] ^= k
        x += lowbit(x)

def query(x):
    res = 0
    while x:
        res ^= tr[x]
        x -= lowbit(x)
    return res

5.2 线段树（c++模板）

inline void pushup(ll p) { ans[p]=ans[lch(p)]+ans[rch(p)]; }
inline void build(ll l,ll r,ll p)
{//递归建树 
	if(l==r) { ans[p]=a[l]; return ; }
	ll mid=(l+r)>>1;
	build(l,mid,lch(p));
	build(mid+1,r,rch(p));
	pushup(p);//从叶子节点向上统计信息 
}
inline void f(ll l,ll r,ll p,ll k)
{//f函数用来打懒惰标记+更新区间信息 
	tag[p]+=k;
	ans[p]+=k*(r-l+1);
}
inline void pushdown(ll l,ll r,ll p)
{
	ll mid=(l+r)>>1;
	f(l,mid,lch(p),tag[p]);
	f(mid+1,r,rch(p),tag[p]);
	tag[p]=0;//当懒惰标记向下传递后,父节点得删除标记
}
inline void update(ll l,ll r,ll nl,ll nr,ll p,ll k)
{
	if(nl<=l&&r<=nr)
	{//如果当前区间包含于更新区间,则直接更新当前区间信息
		tag[p]+=k;
		ans[p]+=k*(r-l+1);
		return ;
	}
	pushdown(l,r,p);
	ll mid=(l+r)>>1;
	if(nl<=mid) update(l,mid,nl,nr,lch(p),k);
	//如果更新区间和当前区间的左半部分有交集,则向下更新
	if(nr>mid) update(mid+1,r,nl,nr,rch(p),k);
	//如果右半部分有交集 
	pushup(p);//对更新区间内的元素全部更新完后,再向上统计信息 
}
inline ll query(ll l,ll r,ll ql,ll qr,ll p)
{
	ll res=0;
	if(ql<=l&&r<=qr) return ans[p];
	//如果当前区间包含于查询区间,则直接返回答案
	ll mid=(l+r)>>1;
	pushdown(l,r,p);
	if(ql<=mid) res+=query(l,mid,ql,qr,lch(p));
	if(qr>mid) res+=query(mid+1,r,ql,qr,rch(p));
	return res;
}

6 算法基础和常用函数

6.1 浮点数二分

l, r = 0, float('inf')
while r - l > 1e-8: # 保留位数再右移三个小数点
    mid = (l + r) / 2
    if check():
        l = mid
    else:
        r = mid
return l

6.2 常用函数

# 加深递归深度
import sys
sys.setrecursionlimit(int(1e6))
# 记忆化
from functools import lru_cache
@lru_cache(maxsize=None)
# 二分查找
from bisect import bisect_left, bisect_right
bisect_left # 大于等于查找元素的下标
bisect_right # 大于查找元素的下标
# 二进制转化
bin(x)[2:]
# 优先队列
from queue import PriorityQueue
# 双端队列、栈
from collections import deque
# 计数器和好使的字典
from collections import Counter, defaultdict